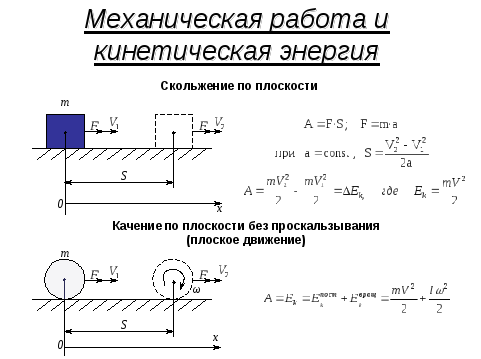
Физические основы механики

Рассмотрим теперь плоское движение твердого тела, то есть движение, при котором точки тела описывают траектории, лежащие в параллельных плоскостях. Пример такого движения — вращение колеса автомобиля при его движении по прямой. Можно взять любую точку 0 тела и мысленно провести через нее ось вращения перпендикулярно плоскостям, в которых лежат траектории точек тела. Тогда ось вращения будет двигаться поступательно, оставаясь все время параллельной самой себе.

Видео 7.2. Плоское движение твердого тела в однородном поле тяжести. Полет плоской картонной фигуры

Соответственно, скорость элементарной массы твердого тела складывается из скорости поступательного движения точки 0 и линейной скорости вращения вокруг связанной с ней (мысленно проведенной) оси:

где — радиус-вектор, определяющий положение элементарной массы по отношению к точке 0.

Кинетическая энергия элементарной массы равна тогда:

Векторное произведение

имеет модуль, равный , где — расстояние массы от оси вращения. Следовательно, третье слагаемое в скобках равно . Второе слагаемое, представляющее собой смешанное произведение векторов, не меняется при циклической перестановке сомножителей:

В результате получим для кинетической энергии элемента твердого тела следующее выражение

Для нахождения кинетической энергии тела просуммируем по всем элементарным массам:

Сумма элементарных масс

есть масса твердого тела. Выражение

где — радиус-вектор центра масс тела относительно точки 0.

Наконец,

— есть момент инерции тела относительно оси вращения. Поэтому для кинетической энергии твердого тела можно записать формулу:

Поскольку выбор мысленной оси вращения всецело в нашей власти, мы упростим полученное выражение, взяв в качестве точки 0 центр масс тела. Тогда = 0 и кинетическая энергия тела при плоском движении равна

Здесь — скорость движения центра масс, a — момент инерции относительно оси, проходящей через центр масс и ортогональной плоскости, где лежат траектории точек тела. Таким образом, кинетическая энергия твердого тела при плоском движении слагается из энергии поступательного движения со скоростью, равной скорости центра масс и энергии вращения вокруг оси, проходящей через центр масс тела.

Движение твердого тела определяется действующими на тело внешними силами и моментами этих сил

Индекс в обозначениях для момента внешней силы означает проекцию момента на ось вращения.

В следующих примерах мы имеем дело с плоским движением.

Видео 7.3. Зависимость поведения цилиндров на наклонной плоскости от характера распределение массы по их объему

Пример 1. Круглое однородное тело (обруч, цилиндр, шар) радиусом и массой скатывается без скольжения по наклонной плоскости под углом к горизонту с высоты (рис. 7.12). Начальная скорость тела равна нулю. Найдем скорость центра масс каждого тела в конце спуска.

Рис. 7.12. Скатывание тела с наклонной плоскости

Рассмотрение данной задачи можно вести двумя способами.

1-й способ. По условию тело катится без проскальзывания. Это условие используется у нас дважды. Сила трения между телом и плоскостью действует в точке соприкосновения и в отсутствие скольжения не превышает своего максимального значения:

где — коэффициент трения скольжения.

Оси координат удобно направить следующим образом: ось х — вдоль движения, ось у — перпендикулярно наклонной плоскости. Тело движется под действием трех сил: силы тяжести , силы трения и силы нормального давления , так что уравнение поступательного движения центра инерции тела имеет вид:

Вдоль оси у тело не движется. Проецируя уравнение движения центра масс на ось у, получаем для силы нормального давления соотношение:

Проекция уравнения движения на ось х дает:

Так как линейная скорость точек соприкосновения цилиндра с наклонной плоскостью равна нулю (опять используем условие отсутствия проскальзывания), то скорость (ускорение) поступательного движения связаны с угловой скоростью (угловым ускорением) тела обычными соотношениями:

Кроме поступательного движения, тело еще и вращается.

Вращение удобно описывать относительно оси z, проходящей через центр масс цилиндра.

Выбор этот обусловлен тем, что линии действия силы тяжести и силы нормального давления плоскости проходят через ось вращения и, следовательно, моменты этих сил равны нулю. Таким образом, цилиндр вращается только под действием силы трения, и уравнение вращательного движения имеет вид:

Таким образом, получается система 4-х уравнений, описывающих поступательное и вращательное движение с дополнительным неравенством, выражающим закон трения. Решая систему уравнений, находим:

Чем больше момент инерции относительно оси, проходящей через центр масс, тем меньше ускорение тела. Мы уже получили ответ на один из вопросов задачи: шар будет двигаться быстрее цилиндра, а цилиндр — быстрее обруча. Подставляя решение для силы трения в неравенство, выражающее закон трения, находим условие, при котором будет отсутствовать проскальзывание:

Смысл этого условия прост: наклон не должен быть слишком крут.

Итак, центр масс тела движется вдоль плоскости с постоянным ускорением a, так что зависимость пройденного пути и скорости от времени имеет вид:

Отсюда следует связь скорости и пройденного пути:

К концу спуска тело проходит путь

так что его скорость достигает величины

Подставляя сюда моменты инерции обруча (), цилиндра () и шара (), находим соответственно:

2-й способ. Используем закон сохранения полной энергии. В конце спуска тело приобретает кинетическую энергию

Эта кинетическая энергия приобретена за счет потенциальной энергии . Отсюда следует найдено выше выражение для скорости тела в конце спуска. Такой способ намного короче, но он не позволяет узнать детали процесса: действующие на тело силы и т.п.

В рассмотренном выше примере мы считали примере мы имели дело со случаем, когда проскальзывание отсутствовало.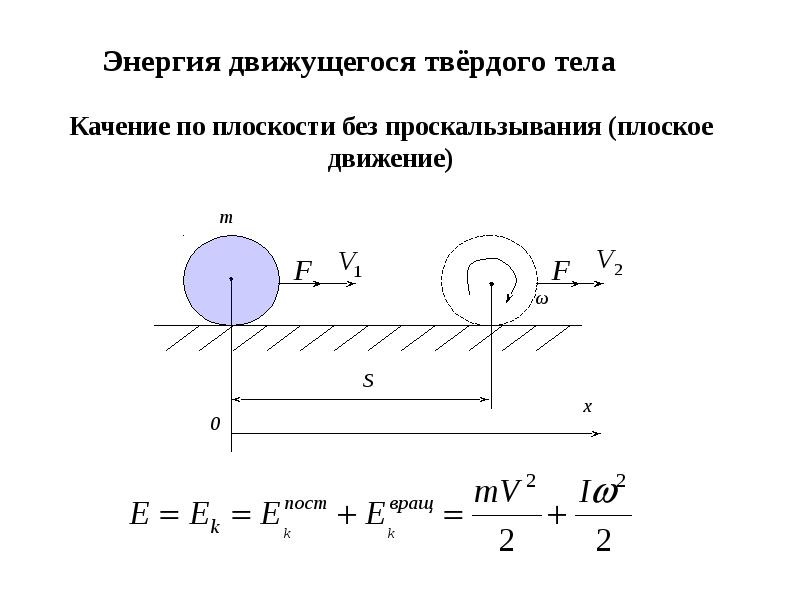 Это позволило утверждать простую связь () между угловой и линейной скоростями тела и его радиусом. Сила трения покоя находилась при этом в результате решения уравнений движения. В случае, когда тело движется с проскальзыванием, заранее известной связи между линейной и угловой скоростями нет. Зато мы заранее знаем силу трения: раз точка соприкосновения тела с поверхностью скользит по поверхности, сила трения есть сила трения скольжения,модуль которой связан с силой нормального давления законом Амонтона — Кулона.

Силы трения, как уже говорилось, направлены так, чтобы препятствовать относительному проскальзыванию

соприкасающихся тел. Часто путают это возможное проскальзывание с осуществляемым поступательным движением. Необходимо четко понимать, что не редки случаи, когда сила трения не тормозит, но ускоряет тело, то есть направлена по его движению. Самый известный пример — трогание автомобиля с места. Колеса начинают вращаться и проскальзывают по земле назад. Соответственно, сила трения направлена вперед, и именно она заставляет автомобиль трогаться. Чтобы ближе познакомиться с подобными случаями, рассмотрим пример.

Пример 2. Цирковой артист бросает на арену обруч массой и радиусом , который начинает катиться в горизонтальном направлении со скоростью (рис. 7.13). При этом обручу придано обратное вращение с угловой скоростью . Найдем, при какой угловой скорости обруч после остановки покатится назад к артисту, а также конечную скорость поступательного движения обруча.

Рис. 7.13. Движение обруча с обратным вращением

При обратном вращении обруча точка его касания с ареной движется вперед как из-за вращения, так и из-за поступательного движения обруча. Поэтому неизбежно существует проскальзывание и, значит, сила трения достигает своего максимального значения. Она тормозит как поступательное движение, так и вращение обруча. Может случиться так, что поступательное движение обруча будет остановлено в тот момент, когда он еще сохраняет обратное вращение. Далее сила трения начнет ускорять обруч по направлению к артисту. Ускорение это прекратится, когда исчезнет тенденция к проскальзыванию, после чего обруч покатится назад равномерно с некоторой установившейся скоростью . Может, однако, случиться и так, что раньше будет остановлено обратное вращение, и тогда обруч сохранит поступательное движение вперед, изменив направление вращения на прямое. Чтобы различить эти два случая, качественных рассуждений недостаточно, и мы обратимся к формулам.

Направим ось ОХ направо (в направлении красной стрелки на рис. 7.13), ось вращения ОZ направим на нас (см. следующий пример, там эту ось удобнее направить от нас, то есть за чертеж), то есть в направлении «обратного» вращения, ось OY направим как обычно, вверх. Плоское движение обруча представим как суперпозицию его поступательного движения вместе с центром масс (геометрическим центром, поскольку обруч предполагается однородным). Спроектируем линейные и угловые скорости на соответствующие оси. Тогда, до тех пор, пока сила трения есть сила трения скольжения и направлена она налево, уравнения движения имеют вид

(7. 3.1)

(7.3.2)

Уравнение (7.3.1) описывает движение центра масс обруча, а уравнение (7.3.2) его вращение вокруг оси проходящей через центр масс в той системе отсчета, в которой она покоится (системе центра масс). В (7.3.2) учтено, что момент инерции однородного обруча относительно его оси симметрии равен . После элементарного интегрирования получаем

(7.3.3)

(7.3.4)

Поступательное движение прекратится, то есть станет равным нулю, в момент времени

(7.3.5)

Вращение прекратится, то есть станет равным нулю,в момент времени

(7.3.6)

Их отношение

(7.3.7)

может быть любым ввиду независимости начальных скоростей поступательного и вращательного движений.

Для дальнейшего анализа введем в рассмотрение скорость нижней точки обруча — той его точки, которая касается поверхности арены. Отметим уже здесь, что условием исчезновения проскальзывания является обращение в ноль скорости именно этой точки, потому что скорость соответствующей точки на поверхности арены (той, которой касается обруч) очевидным образом в нашей системе отсчета, где арена неподвижна, равна нулю. Отсутствие проскальзывания это и есть неподвижность этих двух точек относительно друг друга. При выбранном направлении осей OZ и OX, имеем

(7.3.8)

Если , то первым прекратится поступательное движение обруча. В момент времени скорости (7.3.3) и (7.3.8) будут иметь значения

Нижняя точка обруча, за счет продолжающегося вращения, будет по-прежнему скользить относительно арены направо (направо на рисунке 7.13), сила трения скольжения сохранит свою величину и направление налево. Соответственно, центр обруча начнет ускорятся налево, то есть станет меньше нуля и начнет расти по модулю, вращение против часовой стрелки (на рисунке 7. 13) будет продолжать замедлятся. Другими словами, при обруч в момент времени (7.3.5) начинает возвращаться к бросившему его артисту.

Как следует из (7.3.8), в момент времени

(7.3.9)

скорость нижней точки обруча из (7.3.8) обращается в ноль, проскальзывание прекращается, сила трения скольжения скачком сменяется равной нулю силой трения покоя (силой трения качения пренебрегаем) и обруч начинает катится к артисту с постоянной скоростью движения центра масс

(7.3.10)

вращаясь против часовой стрелки с постоянной угловой скоростью

(7.3.11)

Если , то первым, в момент времени (7.3.6), прекратится вращение обруча. В момент времени скорость (7.3.8) нижней точки обруча будет равна скорости его центра и положительна:

(7.3.12)

Скольжение остается, сила трения скольжения сохраняет свою величину и направление налево, но обруч под действием этой силы трения скольжения начинает вращаться по часовой стрелке (напоминаем: налево, направо, по или против часовой стрелки — на рисунке 10). В результате этого скорость центра масс (центра обруча) будет уменьшаться, скорость вращения увеличиваться, в момент времени

(7.3.13)

проскальзывание обруча прекратится и обруч начнет равномерно удаляться от артиста со скоростью центра (7.3.10) и угловой скоростью вращения (7.3.11). Напомним, что в этом случае , так что а

Таким образом, ответ на вопрос: «Вернется обруч или укатится?» определяется начальными условиями, а конкретнее величиной параметра , который имеет простой физический смысл: это отношение модуля

скорости любой точки обруча за счет его поступательного движения вместе с центром масс к модулю скорости той же точки за счет вращения обруча вокруг оси, проходящей через его центр масс, в начальный момент времени.

Пример 3. Описать движение обруча (см. предыдущий пример), если ему придано прямое вращение (рис. 7.14). Поскольку обруч вращается теперь на рис. 7.14 по часовой стрелке, направим ось вращения OZ от нас, то есть за чертеж — в отличие от предыдущего случая.

Рис. 7.14. Движение обруча с прямым вращением: 1 – ; 2 –

Начальная скорость нижней точки обруча складывается из скорости поступательного движения и линейной скорости за счет вращения, направленной в противоположную сторону. В связи с этим надо различать два случая.

1 случай или . Тогда начальная скорость нижней точки обода положительна, то есть, направлена в ту же сторону, что и скорость . Значит, сила трения f направлена в противоположную сторону, как показано на рис. 11–1. В связи с изменением положительного направления оси вращения необходимо лишь изменить знак перед вторым слагаемым в уравнении (7.3.4). Решение уравнений движения в рассматриваемом случае имеют вид

(7.3.14)

(7.3.15)

При новом выборе направления оси вращения скорость нижней точки обруча записывается в виде

(7.3.16)

Момент исчезновения проскальзывания определится из того же соотношения равенства нулю скорости нижней точки обруча или равенства по модулю противоположно направленных скоростей этой точки за счет поступательного движения вместе с центром масс и вращательного движение вокруг оси, проходящей через центр масс:

откуда находим:

Скорость поступательного движения обруча в этот момент становится равной

и остается потом неизменной. Эта скорость меньше начальной скорости поступательного движения обруча.

2 случай или . В этом случае скорость нижней точки обода отрицательна, направлена против скорости . Значит, сила трения направлена по (см. рис.11-2).

Соответственно, в уравнениях движения и их решениях (7.3.14) и (7.3.15) надо изменить знаки на противоположные перед вторыми слагаемыми, содержащими изменившую направление силу трения, получаем:

(7.3.17)

(7.3.18)

Соответственно, выражение для скорости нижней точки обруча приобретает вид:

(7.3.19)

Момент прекращения проскальзывания определяется аналогично и оказывается равным:

а для скорости установившегося движения получается вновь выражение

но в данном случае она будет больше () начальной скорости поступательного движения.

Объединяя оба случая в один, записываем окончательный результат:

Дополнительная информация

http://www. plib.ru/library/book/14978.html Сивухин Д.В. Общий курс физики, том 1, Механика Изд. Наука 1979 г. — стр. 256 (§ 48, задача 9): рассмотрено движение маятника Максвелла, включая силу натяжения нитей подвеса в нижней точке.

http://kvant.mirror1.mccme.ru/pdf/1997/04/kv0497khorozov.pdf — журнал «Квант» — решение задачи об отскоке вращающегося мяча от плоской стенки (С. Хорозов).

http://kvant.mirror1.mccme.ru/pdf/1998/04/kv0498chernoutsan.pdf — журнал «Квант» — применение законов динамики твердого тела в задаче о падении вертикальной палочки на горизонтальный стол (А. Черноуцан).

http://kvant.mirror1.mccme.ru/pdf/1999/02/kv0299chernoutsan.pdf — журнал «Квант» — продолжение задачи о падении вертикальной палочки на горизонтальный стол (А. Черноуцан).

Поворот с проскальзыванием лыж. | Yourski.ru

Теперь вы уже умеете контролировать скорость, двигаться поворотами в плуге с выходом на параллельное движение лыж и можно переходить к следующей стадии развития вашей горнолыжной техники.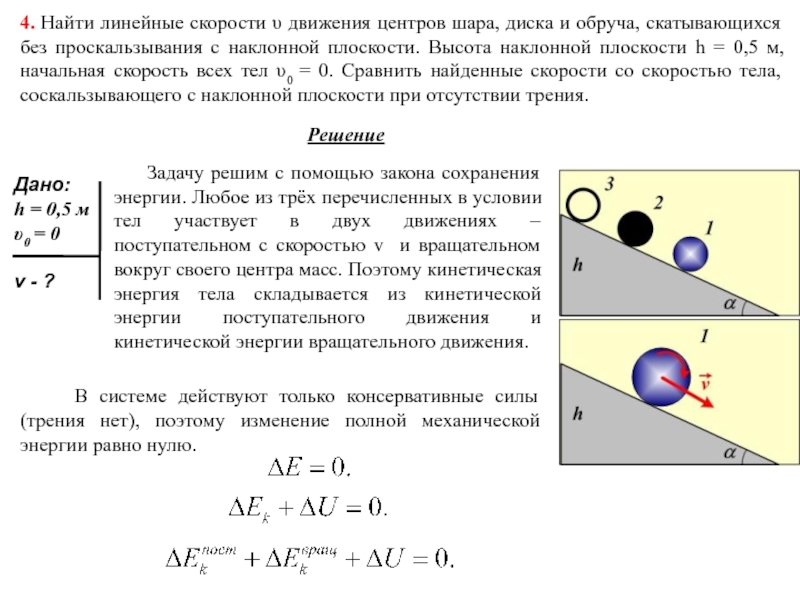 Давайте рассмотрим поворот с полным параллельным ведением лыж без плуга с проскальзыванием лыж. Эта тема по праву может считаться последней в курсе начальной подготовки при обучении технике катания на горных лыжах. 

Делается поворот с проскальзыванием так: Все движения происходят при параллельном ведении лыж. Поворот происходит за счет разворота лыж в сторону поворота и наклона лыж к склону и закантовки что заставляет лыжи цепляться за склон и ехать в сторону в которую вы их направили. Разворот лыж осуществляется посредством разворота корпуса внутрь поворота. Мы не говорили об этом, но само движение неизбежно появляется при выполнении упражнений которые мы описали ранее в этой части самоучителя и вы их должны были поделать. Если вы делали упражнения, то вопросов о том как повернуть лыжи у вас не должно возникать. Он возникает только при изучении катания на диване. Лыжи начинают «скоблить» склон создавая эффект торможения. То есть, обе лыжи едут так, как раньше, когда мы делали поворот в положении плуг, ехала внешняя лыжа.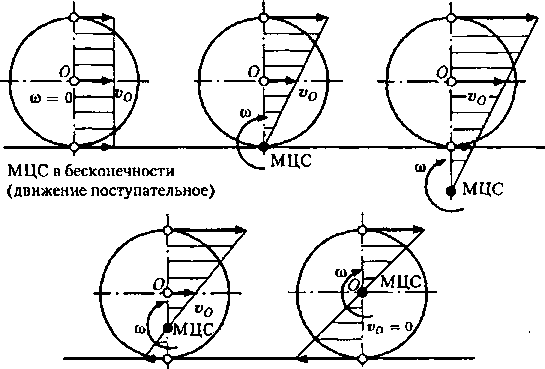  Контроль скорости при таком движении происходит и траекторией движения за счет того, что часть вашего пути направлено поперек склона и проскальзыванием лыж.

Основная задача в том, чтобы уйти от плуга и перейти к полному параллельному ведению лыж, без потери ощущения контроля над движением и скоростью которую нам давал плуг. Такое движение является логическим продолжение предыдущей темы. Вы должны прийти к такому катанию постепенно уменьшая участие плуга в вашем катании поворотами. Сейчас мы просто еще раз уточняем что именно должно получится в финале нашего с вами обучения катанию.

Вот как выглядит наша траектория движения и положение лыж в этой траектории:

На рисунке показаны 2 варианта движения. Давайте разберем оба.

Вариант 1.

Ставим лыжи под углом к траектории движения сразу в самом начале движения в повороте. Разворот лыж в начале поворота дает нам то, что мы не разгоняемся вообще. То есть, движение в повороте происходит медленно и контролируемо с самого начала поворота. Такой вариант предпочтителен для людей с чрезмерно развитым инстинктом самосохранения и не ленивых. Потому как физически такой поворот делать сложнее. Лыжи лучше проскальзывают на скорости.

Вариант 2.

Начинаем движение в повороте с продольным скольжением лыж, а при выходе из поворота, когда наша скорость несколько увеличилась, гасим ее ставя лыжи, разворачивая корпус внутрь поворота, под углом к линии траектории нашего движения. Такой способ проще и дает больше полезных ощущений нужных для дальнейшего изучения горнолыжной техники.

Вот как это делается:

Не торопитесь и старайтесь делать не спеша, но правильно. Основная задача — научиться двигаться по ровной и системной S-траектории. Научитесь полностью контролировать скорость. И помните: движение на проскальзывающих лыжах не дает 100% управляемости траекторией движения. Не лезьте в «авантюры». Может получится так, что лыжи не поедут туда, куда вы хотели ехать или не поедут настолько резко и агрессивно как вам этого хочется. И не надо ругаться на канты и стачивать их «в ноль». Канты тут не при чем. Это просто такая вот техника поворота. Но, на данном этапе обучения она очень эффективна и полезна для вас. Старайтесь избегать ледяных участков. Данная техника не способна обеспечивать комфортное катание на ледяных склонах. Лыжи тут не при чем. 

Плоское движение. Качение — Энциклопедия по машиностроению XXL

Обратимся к классическому простому примеру плоского движения — качению цилиндра по плоскости без проскальзывания. Рассматривая одно из сечений цилиндра плоскостью, перпендикулярной его оси, мы придем к известной задаче о катящемся колесе (рис. 1.10). Центр колеса движется прямолинейно, траектории других точек представляют собой кривые, называемые циклоидами.  [c.11]

Решение. Катушка совершает плоское движение. Так как качение происходит без скольжения, то мгновенный центр скоростей  [c.314]

В заключение отметим, что если плоское движение фигуры осуществляется путем качения ее без скольжения по некоторой неподвижной линии (как, например, на рис. 92), то контур фигуры и эта линия будут соответственно подвижной и неподвижной центроидами и, следовательно, точка их касания будет мгновенным центром вращения. Для определения скорости любой точки фигуры надо в этом случае знать только скорость какой-нибудь одной из ее точек.  [c.109]

При плоском движении фигуры подвижная центроида катится без скольжения по неподвижной центроиде. Эта теорема позволяет плоское движение твердого тела рассматривать как качение без скольжения одной плоской кривой по другой.  [c.161]

Диск О совершает плоское движение. К нему приложены сила тяжести Р, реакция нити 8 и реакция рельса, состоящая из нормальной реакции Ы, силы трения Р и пары сил, препятствующей качению с моментом В (рис. 80). Силу трения Р предполагаем направленной в положительную сторону оси Ох.  [c.341]

Рассмотрим, наконец, более сложный пример, в котором плоское движение осуществляется качением кривой второго порядка по кривой четвертого порядка.  [c.205]

Рассмотрим простейший случай движения твердого тела, не имеющего закрепленных точек, именно случай плоского движения, при котором каждая точка твердого тела движется, оставаясь в одной из параллельных друг другу плоскостей. Примером этого типа движений может служить качение цилиндра по плоскости.  [c.417]

Решение. Колесо совершает плоское движение. Его мгновенный центр скоростей находится в точке контакта Р колеса с рельсом, так как качение осуществляется без скольжения. Зная положение мгновенного центра скоростей и скорость точки О колеса, найдем его угловую скорость  [c.58]

Аналогично эта модель строится для плоских движений осесимметричных тел (например, для качения диска по кривой). При этом вектор = перпендикулярен плоскости движения.  [c.72]

Третье уравнение плоского движения колеса найдем, приравняв перемещение центра колеса точки В произведению угла поворота колеса на радиус вращения Ь (это верно при качении колеса по плоскости без скольжения (рис. а))  [c.549]

Плоское движение прямого угла АМК можно представить как качение без скольжения подвижной центроиды (параболы с фокусом А) по неподвижной центроиде (параболе с фокусом в точке В).  [c.558]

Анализ движения тела при любом положении точки приложения силы к твердому телу представляет довольно сложную задачу. Поэтому рассмотрим сначала плоское движение тела, при котором все частицы тела движутся параллельно определенной плоскости. Например, движение ящика по гладкой и ровной поверхности льда, движение коробки по поверхности стола, качение цилиндра, качение колеса и т. п.  [c.200]

В качестве примера плоского движения рассмотрим качение цилиндра или колеса по плоскости.  [c.206]

При изучении динамики плоского движения твердого тела, решая обычно задачу о движении колеса, учим студентов понимать динамическое условие качения без проскальзывания и качения с проскальзыванием, учим подсчитывать работу сил, приложенных к твердому телу, совершающему плоскопараллельное движение. Большую роль в усвоении раздела играет домашнее задание, охватывающее все общие теоремы динамики.  [c.11]

Теорема о кинетическом моменте в общей форме (5) может быть с успехом использована в ряде задач, которые не решаются с помощью других форм этой теоремы. Пример задачи такого рода — задача о качении однородного цилиндра по наклонной плоскости (рис, 2). Обычно эта задача решается с помощью трех дифференциальных уравнений плоского движения твердого тела. Но при качении без скольжения цилиндр имеет одну степень свободы и для определения его движения вовсе не обязательно составлять три дифференциальных уравнения. Применяя в данной задаче теорему о кинетическом моменте в форме (5), выберем за центр О точку, совпадающую в любой момент времени с мгновенным центром скоростей цилиндра, т. е. точку касания его с плоскостью . Эта точка движется вдоль плоскости со скоростью г о, равной скорости центра масс С. Следовательно, при таком выборе  [c.7]

Примером плоского движения тела может служить качение цилиндра по горизонтальной плоскости, при котором его основание остается все время параллельным плоскости уг (рис.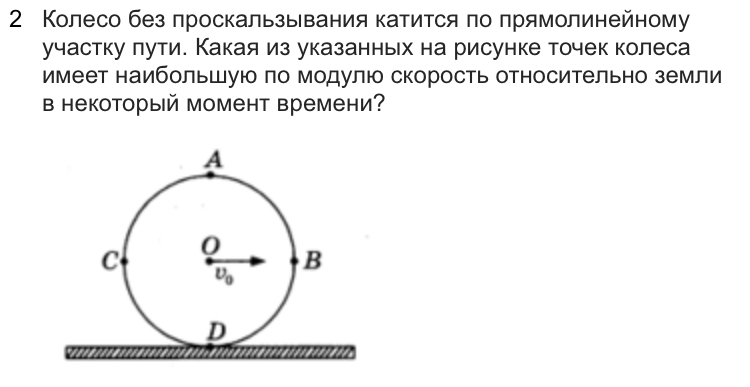 11.1).  [c.193]

В каждый момент времени подвижная и неподвижная центроиды имеют общую точку касания—мгновенный центр скоростей Р, т. е. точку, скорость которой равна нулю. Поэтому плоское движение можно представить, как качение без скольжения подвижной центроиды по неподвижной.  [c.204]

По закону Кулона сила трения скольжения при движении имеет вполне определенное направление, противоположное скорости относительного скольжения, и вполне определенную вели- чину, пропорциональную нормальной реакции Р = 1М, где / — коэффициент трения скольжения при движении сила трения скольжения при покое может иметь любое направление в касательной плоскости, а ее величина может принимать любое значение, удовлетворяющее где о — коэффициент трения скольжения при покое, причем / [о- При качении без скольжения сила трения скольжения находится так же, как при покое. Мы вернемся к этому вопросу в гл. УИ при рассмотрении плоского движения пока же отметим только следующее если, например, диск катится без скольжения по прямой, то это условие упрощает кинематику, ибо мгновенный центр скоростей должен совпадать с точкой касания, но усложняет динамику, ибо сила трения скольжения не имеет определенного значения, а должна удовлетворять только приведенному выше неравенству.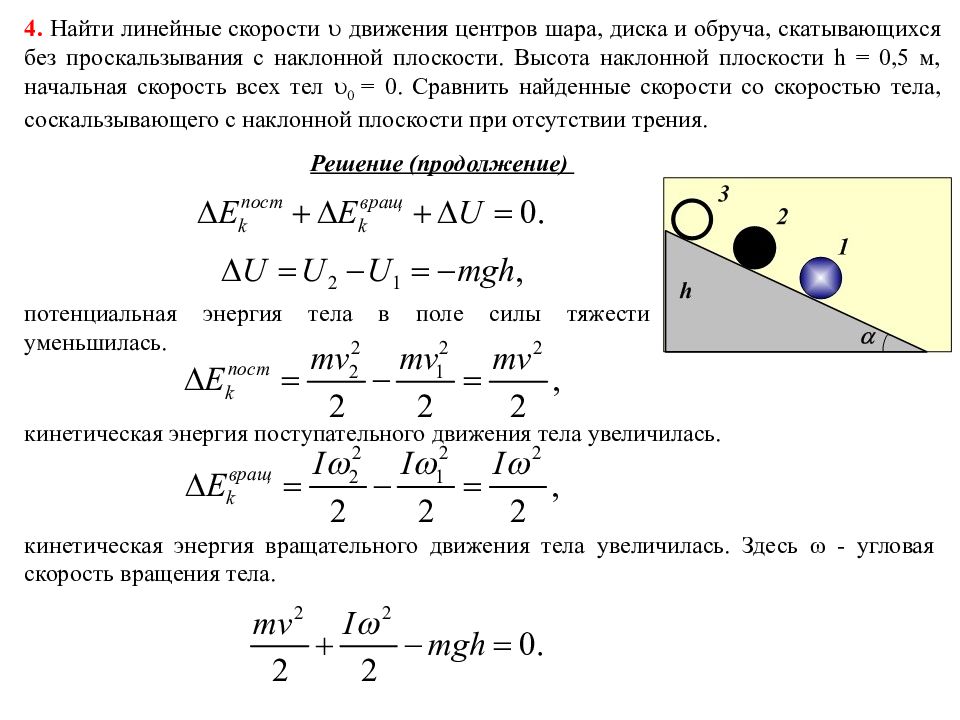 Если же не ставить условия качения без скольжения, то усложнится кинематика, ибо мы теперь не знаем положения мгновенного центра скоростей, но упростится динамика, ибо в этом случае сила трения скольжения имеет вполне определенное значение.  [c.74]

Условия ЗАДАЧ. Механическая система с одной степенью свободы состоит из тел, совершающих плоское движение. Под действием сил тяжести система из состояния покоя приходит в движение. Какую скорость приобретет груз А, переместившись вверх или вниз) на S = 1 ш Качение цилиндра (или блока) происходит без проскальзывания с коэффициентом трения качения 6. Коэффициент трения скольжения Радиусы инерции г , Внешние радиусы Rq, Rjj, внутренние г , г .  [c.268]

Совершенно ясно, что если известны центроиды некоторого плоского движения, то мы можем восстановить геометрическую картину истинного движения плоской фигуры качением без скольжения подвижной центроиды по неподвижной.  [c.119]

Как и для плоского движения, отметим, что с помощью аксоидов при произвольной скорости качения подвижного аксоида по неподвижному мы воспроизводим действительное движение абсолютно твёрдого  [c.326]

Различают механизмы с высшими парами чистого качения и механизмы, где имеет место качение со скольжением. Чистое качение характеризуется тем, что мгновенный центр вращения профиля одного звена относительно профиля другого все время совпадает с последовательно соприкасающимися точками профилей при идеальной твердости последних. Для качения со скольжением характерно представление о плоском движении, где скорость перемещения точки одного звена по поверхности другого  [c.230]

Подвижные приводные муфты действуют посредством скользящего движения или движения качения криволинейных передач или передач с соединительным звеном, а именно как соединения подвижные в поперечном направлении по отношению к валам — посредством плоского криволинейного или шатунного механизма как подвижные с угловым перемещением в отношении валов — посредством сферического, и как подвижные во всех направлениях по отношению к валам — посредством пространственного криволинейного или шатунного механизма (см. выше стр. 380, табл. 16, и стр. 396, табл. 18).  [c.484]

Плоское движение, как следует из определения центроид, может быть представлено как качение без скольжения подвижной центроиды по неподвижной.  [c.103]

Итак, всякое плоское движение может быть представлено как качение без скольжения некоторой подвижной кривой, неизменно связанной с плоской фигурой, по некоторой неподвижной кривой.  [c.241]

Пара IV класса в плоском механизме исключает возможность одного какого-либо движения например, пара, показанная на рис. 2.9, исключает относительное движение звеньев Л и В в направлении нормали п — ПК кривым а — аир — р, проведенной в точке их касания. Возможными двумя относительными движениями звеньев этой пары являются качение и скольжение одной кривой по другой.  [c.41]

Таким образом, при движении плоской фигуры в ее плоскости подвижная центроида MN катится без скольжения по неподвижной центроиде KL (рис. 321). Точка соприкасания подвижной центроиды с неподвижной центроидой является в данный момент времени мгновенным центром скоростей. Это положение представляет собой теорему Пуансо о качении подвижной центроиды по неподвижной, которая имеет следующую формулировку  [c.243]

Решение. Движение линейки АВ плоское, а следовательно, оно может быть осуществлено качением подвижной центроиды по неподвижной. Примем прорези крестовины за оси основной системы координат хОг/. Подвижную систему координат х Еу свяжем с линейкой, взяв за начало ее середину Е. Мгновенный центр скоростей находится на пересечении перпендикуляров, восставленных к скоростям точек Л и В (см. задачу № 89), и, как видно из чертежа, находится на расстоянии 0Е = 1 от точки О  [c.231]

В первом томе рассматриваются следующие разделы статики и кинематики система сходяптихся сил, произвольная плоская система сил, равновесие тел при наличии трения скольжения и трения качения, графическая статика, пространственная система сил, центр тяжести движение точки, поступательное движение и вращение твердого тела вокруг неподвижной оси, сложное движение точки, плоское движение твердого тела, вращение твердого тела вокруг неподвижной точки, общий случай движения твердого тела, сложение вращений твердого тела вокруг параллельных и пересекающихся осей, сложение поступательного и вращательного движений твердого тела.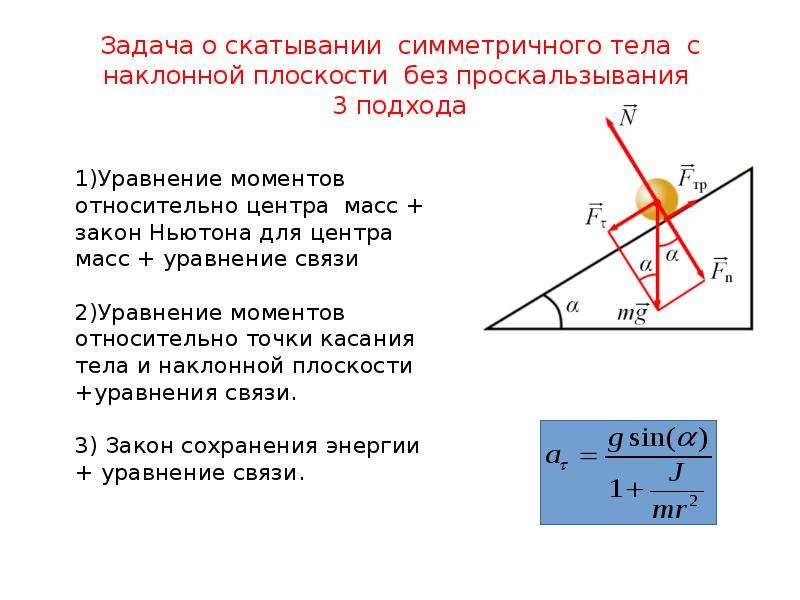  [c.2]

Угловое ускорение (ф) с помощью уравнений движения можно выразить через параметры диска и состояния степенью свободы. Из уравнений плоского движения с удерживаюи(ей связью х = Rip и напряженной неудерживающей связью у = 0) находятся также нормальная составляющая (N) и касательная составляющая (F) реакции в точке контакта. Причем N = О, когда вместо неравенства (1.157) выполняется равенство левой и правой частей.  [c.65]

Решение. Состави.м уравнения двихсения отдельных тел под действием сил. Диск О совершает плоское движение. К нему приложены сила веса Р, реакция нити 5 и реакции рельса, состоящие из нормальной реакции Л, силы трения Р п пары сн.. 1, препятствующей качению с моментом I (рис. 250). Силу трения В предполагаем направленной в положительную сторону оси Ох.  [c.315]

Доказанная теорема о качении аксоидов представляет собой обобщение ранее выведенной в главе о плоском движении теоремы о качении без скольжения подвижной центроиды по неподвижной. Собственно говоря, и в случае плоского движения приходится иметь дело с качением аксоидов, но аксопдов цилиндрических. Сводя задачу к плоской, естественно вместо аксоидов брать следы их пересечения с плоскостью движения — центроиды.  [c.276]

К задаче о плоском движении тве 1дого тела сводятся и все про-стейише случаи качения тел. Однако в этих случаях существенную роль играют силы трения со всеми их специфическими особенностями. Мы рассмотрим несколько н[)имеров качения тел. На цилиндр радиуса г и массы т, скатываюгцийся с наклонной плоскости (рис. 211), действуют две силы сила тяжести mg и сила действующая со стороны наклонной плоскости. Ра.зложим эту силу на две составляющие нормальную т. е. силу нормального давления со стороны  [c.428]

И. Прежде чем обратиться к дальнейшим выводам общего характера, рассмотрим несколько примеров разыскания полярных траекторий заданных плоских движений. К этого рода задачам мы приходим всякий раз, когда хотим механическим приспособлением осуществить то или иное заданное плоское твердое движение. Как мы видели, это всегда возможно выполнить (помимо чисто практических трудностей, на которых мы ниже такл- е остановимся) качением одной из двух полярных траекторий по другой. В прикладной механике особый интерес имеют так называемые эпициклические движения, соответствующие тому случаю, когда обе траектории представляют собою окружность. Этими движениями мы займемся обстоятельно й 8. Здесь же рассмотрим несколько примеров, в которых будем предполагать известной только последовательность полоясений движущейся фигуры, а не закон, которому движение следует во времени. Таким образом, по существу, речь будет итти о вопросах геометрии движения если мы при этом будем иногда вводить  [c.226]

Все эти подвески (кроме корзиночной) обеспечивают перемещение наконечника по сфере, которое при малых отклонениях приближенно можно считать плоским. Строго плоское движение обеспечивают безрычажные подвески, в которых наконечник в виде диска, перекатывающегося по проверяемой цоверхности, смещается либо в направляющих качения 3 — рис. 3, б, либо в направляющих скольжения 1 и. 2 — рис. 3, в [10]. В обоих случаях в центре диска имеется коническое гнездо — первый элемент механизма модульного преобразования.  [c.211]

Итак, показано, что любое плоское движение звена механизма можно реализовать в результате качения полоид друг по другу без скольжения.  [c.156]

Кинематическая структура станка нарезания прямозубого конического колеса по методу обкатки состоит из двух формы зуба пошлине (Я1). Если резцу 2,  [c.168]

В случае движения диска наиболее изучены регулярные прецессии и их устойчивость [122]. В книге [122] исследована также устойчивость вертикальных плоских движений тяжелого эллиптического диска, уравнения которого, вообще говоря, неинтегрируемы. Отметим также, что при полном отсутствии проскальзывания (в классической неголономной постановке) уравнения качения круглого диска также являются интегрируемыми (задача Чаплыгина, Аппеля, Кортевега [2, 122]), однако описываемая ими динамика существенно сложнее.  [c.236]

Вторая публикация О движении одной линии по другой и о трех его разновидностях — скольжении, качении и сложном движении (A ta eruditorum) предвосхищает работы Л. Пуансо, сводящие плоское движение твердого тела к движению подвижной центроиды по неподвижной. Лейбниц показывает, что при качении одной кривой (тела) по другой без проскальзывания подвижная кривая поворачивается около точки контакта (через 100 лет названной Пуансо мгновенным центром скоростей). Кроме этого, при некоторых условиях, у подвижной фигуры существует точка, траектория которой совпадает с неподвижной кривой.  [c.130]

Качение. Частным случаем плоского движения является качение тал, которое обсудим на примере качения однородного цилиндра по горизонтальной плоскости (рис. 63). Качение может происходить со скольжением (с «пробуксовкой»), но мы ограничимся рассмотрением качения без екольжеадя, когда обеспечено такое сцепление между цилиндром и плоскостью, что точки цилиндра, находящиеся на линии его соприкосновения с плоскостью (точка А на рис. 63 а) покоятся относительно плоскости. Ско-  [c.74]

Пример 40. Цилиндрический каток диаметром 0,5 м вкатывается на наклонную пло>, коС 1ь. имея в начальный момент скорость точек оси 1,4 м/с. Угол наклона плоскости к горизонту равен 30 , коэффициент трения качен)1я равел 0,5 см. Определить путь, пройденный осью катка до Остановки, предполагая, что каток катится по наклонной плоскости без скольжения, Решейие, К плоскому движению катка применим теорему об изменении кинетической энергии г ([c.416]

В кулачковых плоских и пространственных механизмах, широко применяемых в различных машинах, станках и приборах, высшая пара образована звеньями, называемыми — кулачок и толкатель (звенья I и 2 на рис. 2.9). Замыкание высшей пары может быть силовое (например, пружиной 5 на рис. 2.9,6) или геометрическое (ролик 3 толкателя 2 в пазу кулачка / на рис. 2.9,а). Форма входного звена — кулачка определяет закон движения выходного звена — толкателя ролик применяют с целью уменьшить трение в механизме путем замены трения скольжения в высшей паре на трение качения. На рис. 2.9,а вращательное движение входного звена (кулачка I) преобразуется в возвратно-поступательное движение выходного звена (толкателя 2). В механизме, изображенном на рис. 2.9, б, толкатель 2 — коромыс-ловый, совершающий возвратно-вращательное движение вокруг оси Оа. На рис. 2.9,в изображена модель пространственного кулачкового механизма с вращающимся цилиндрическим кулачком / и поступательно движущимся роликовым толкателем 2 замыкание высшей пары — геометрическое. На рис. 2.1,а дан пример применения кулачкового механизма с коромысловым (качающимся) роликовым толкателем 5 для привода выхлопного клапана 6, через  [c.30]

Высшая кинематическая пара (рис. 7.10) в плоском механизме допускает два относительных движения звенья / и 2 могут скользить (v 2) И перекатываться друг по другу ( oi2). Поэтому и трение в высшей кинематической паре проявляется двояко в виде трения скольжения и трения качения. Тормозящее действие трения качения (Мк и,) в большинстве случаев весьма невелико, и поэтому его в дальнеЙ1пем учитывать не будем. Конечно, при расчете подшипников качения, при исследовании движения тяжелых предметов на подкладных катках и рольгангах и в других подобных задачах трением качения пренебрегать нельзя. Но такие задачи относятся к области специальных расчетов, а поэтому выходят за рамки учебной ДИСЦИПЛИН1  [c.233]

---

Поворот проскальзыванием

Существует единственный полноценный способ контроля скорости горных лыж (сноуборда и прочих снарядов) на склоне – их боковое движение. При боковом движении сдирается снег, и кинетическая энергия движения отдаётся склону.

Катание на кантах (карвинг, резаные повороты) не обеспечивает полноценного контроля скорости, поскольку скорость уменьшается лишь за счёт удлиннения траектории, а максимальное её удлиннение жёстко определяется характиристиками снаряда и умениями катающегося, таким образом, нижний предел скорости на кантах ограничен. Причём эта минимальная скорость уже для средней крутизны склонов довольно велика – 30-40 км/час, и неприемлема не только для начинающих, для многих туристов она неприемлема в принципе.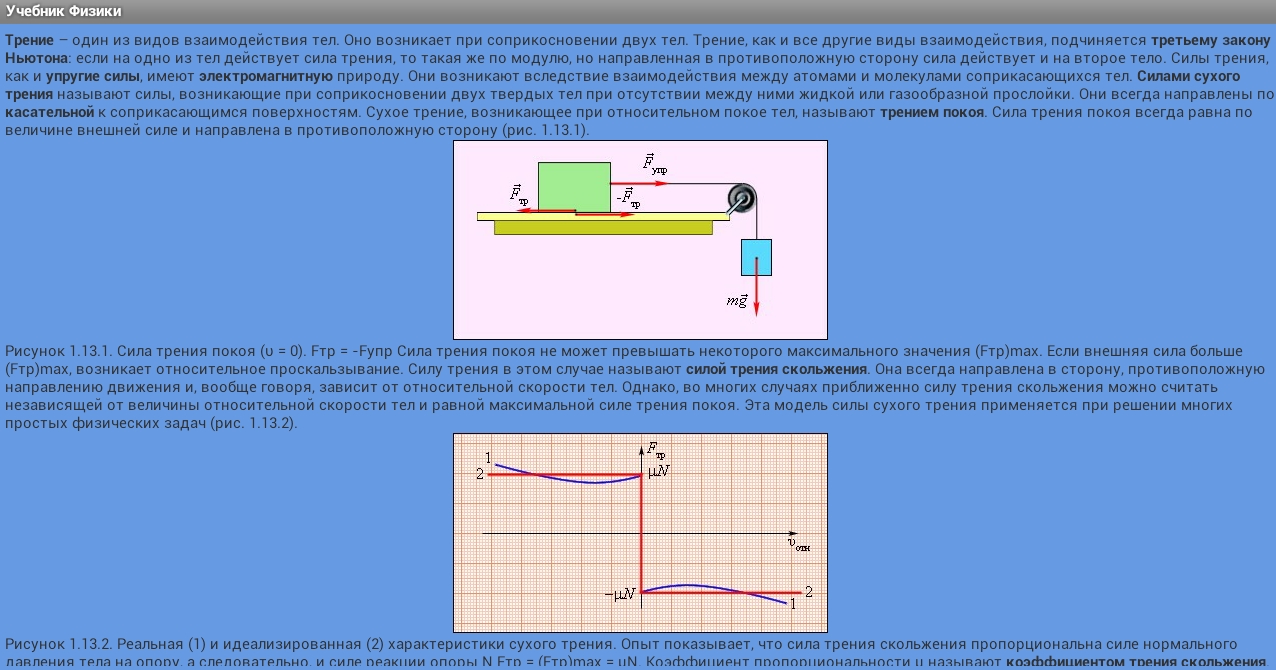 Поэтому в большинстве снежных условий начинать обучение нужно с овладения именно техникой поворотов проскальзыванием.

Современные карвинговые лыжи и сноуборды создали иллюзию простоты управления: поставил на кант – поворачиваешь в одну сторону, поставил на другой – в другую. В реальности же требуется куда большее, и это быстро становится ясным при переходе с пологих (зелёных и синих) склонов на чуть более крутые. Особенно, если склон жёсткий — в таком случае даже на синей трассе большинство псевдокарверов будет терять контроль. Поворот на кантах требует далеко не лишь банальной постановки лыж / сноуборда на кант.

Отсюда простой вывод: хочешь уверенно себя чувствовать на трассах любой крутизны – обучайся технике, использующей боковое движение снаряда – проскальзывание. А недостаточная способность к контролю скорости результат только одного – неумения полноценно пользоваться скользящим поворотом. Такая техника в горнолыжном варианте технического совершенства именуется французским словом “годиль”. Для сноуборда звучное слово «годиль» почему-то не повелось использовать.

И ещё один важный тезис: Каким бы смелым не был начинающий райдер на уровне собственного сознания, подсознание всё равно заставит его сбрасывать скорость, «подметая» склон. Только, не понимая базовой физики управления снарядом, делать он это будет задней частью снаряда, затрачивая излишние усилия и регулярно теряя контроль. Так что вставать на кант, не добившись полноценного контроля в скользящих поворотах, по большому счёту не имеет смысла.

Среди недостаточно информированных начинающих иногда встречается мнение, что скользящий поворот — это не круто, что это «oldschool» и чуть ли не для пенсионеров. Конечно, это не так. В экспертном, конечно, а не в базовом исполнении он позволяет ехать быстро и по очень сложному рельефу. В отличие от карвинга, кстати, которым не на каждом склоне возможно воспользоваться. Для примера годиль (короткие сопряжённые повороты проскальзыванием) на буграх в исполнении нашего инструктора:

С чего бы ни началось обучение, уверенность в контроле скорости возникнет только после выработки автоматизма тонкого навыка контроля угла постановки на кант. Мельчайшая разница в угле постановки на кант приводит к разному результату. На выработку такого навыка уходит от нескольких часов до нескольких дней, и пройти через это неизбежно придётся любому горнолыжнику или сноубордисту. Почему развитие этого навыка требует достаточно много времени? Действительно, по срокам практически все обучающиеся и близко не укладываются в распространённую иллюзию достаточности пары часов занятия с инструктором.

Повспоминайте! Сколько времени уходит у ребёнка, чтобы научиться выводить красивые символы ручкой? Да и стали ли в итоге эти буковки действительно красивыми? А как долго вы учились справляться ложкой и вилкой? Эти, требующие точных движений действия, выполняются мелкими мышцами кисти, в ходе эволюции специально приспособившимися к тонкой работе. Но угол закантовки управляется куда более грубыми мышцами голеностопа. Разве удивительно, что отработка этого навыка требует времени?

Лишь немногие, уже обладающие подходящим развитым автоматизмом, справляются с этой задачей за считанные часы. Это те, кто на хорошем уровне пользуется коньками, роликами, скейтбордом и другими сходными занятиями. Но не спешите впадать в панику! Наша статистика показывает, что даже обладающий самой неразвитой на момент начала занятий координацией человек (с сидячей работой и в возрасте), за стандартный срок выездной школы — 6 дней по 4 часа, успевает освоить этот навык. Просто те, кто осваивает его быстрее, успевают продвинуться дальше.

И это ключ к контролю скорости на склоне любой крутизны. Да, вот так просто.

Но это ещё не всё. Заставить лыжи поворачивать можно разными способами. Эти способы обладают разной эффективностью — требуют различных энергетических затрат, а некоторые из них работают не во всём диапазоне условий. Пожалуй, на сегодняшний день среди профессионалов не будет споров относительно тезиса, что наиболее эффективным способом управления горными лыжами / сноубордом является смещение центра тяжести райдера относительно снаряда в продольном и поперечном направлении.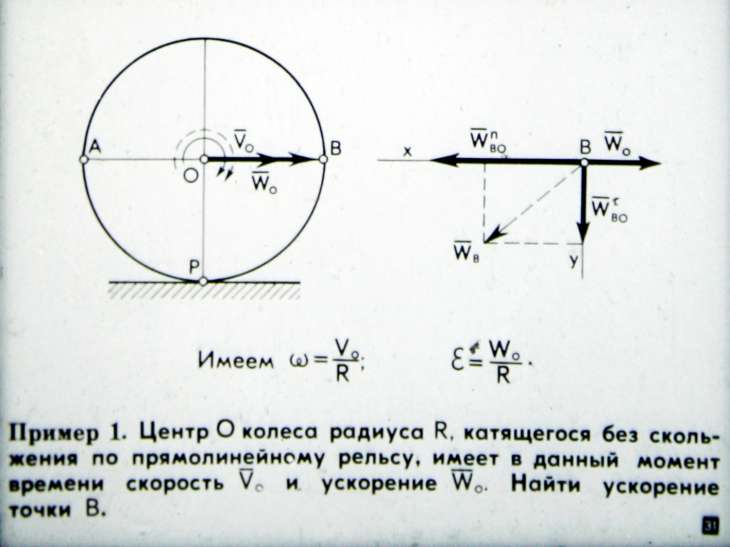 Иными словами — путём изменения баланса. Это не значит, что остальные способы не используются. Но роль их является вторичной.

Поясним сказанное следующим видео. Стоя на плоских, раскантованных лыжах, лыжник переносит центр тяжести вперёд. И… лыжи разворачиваются носками вниз САМИ! Всё, для выполнения простейшего поворота не требуется делать практически ничего, кроме смещения центра тяжести вперёд, а затем возвращения назад, и небольшого изменения закантовки. Все нюансы и пилотаж — это уже потом. Много ли сил и затрат энергии для этого необходимо? Отсюда и максимальная эффективность.

Однако, не следует думать, что выполнить это движение будет просто. Наш ум, всё наше естество против того, чтобы позволить вашему телу падать вниз по склону. Ваш мозг считает это небезопасным, и тем более небезопасным, чем круче склон. Потребуется убедить его, что именно этот вариант самым безопасным и является. Так что для достижение этого результата будет необходимо проделать весь цикл подготовительных упражнений с многократными повторениями, вплоть до достижения автоматизма. Как это происходит, можно наблюдать на следующем ролике с хроникой занятий одной группы.

Кстати, на сноуборде достижение этого результата чуточку сложнее. Сноуборд имеет радиус поворота в полтора-три раза меньше лыж и прям таки рвётся зацепить склон кантом (то, что называют «поймать кант»), а точность при малом угле закантовки нарабатывается сложнее, поскольку в продольном направлении голеностопный сустав менее чувствителен к малым движениям, чем в боковом.

Основное внимание инструктора будет сосредоточено на том, чтобы исключить вращательные (они же ротационные) движения разными частями тела, которые у всех нас развиты до автоматизма для сохранения равновесия «в обычной жизни». Поскольку сами за собой мы практически не замечаем автоматических движений, исключить их влияние довольно непросто, а участие инструктора в течение некоторого времени просто необходимо.

Для прохождения Базового курса поворотов проскальзыванием мы рекомендуем прежде всего наши регулярные выездные курсы в Нечкино. Этот малый курорт имеет отличный сервис при небольшом бюджете и находится в удобной доступности от Москвы, средней полосы и Западной Сибири. А в пакет, предлагаемый курортом Нечкино Прогресс-Ski, включены проживание, катание, питание и даже прокат. Для дальнейшего совершенствования уже интереснее туры в большие горы.

Подготовьте себя к упорным и настойчивым занятиям. Чтобы начать получать удовольствие, сперва нужно постараться. И вот что — мы не форсируем процесс обучения. Безопасность занятий требует, чтобы каждый следующий этап начинался не раньше, чем достигнут автоматизм в выполнении предыдущего. Это так же, как научиться ходить. Поэтому спешить нельзя. Но, когда навык уже закреплён, ноги работают сами, лыжи / сноуборд поворачивают, и даже думать о том, как это происходит, нет необходимости — вы просто думаете «я поеду вот туда», и едете. Шесть дней с Прогресс-Ski и настойчивость — всё, что вам нужно.

Полный список курсов и программ Прогресс-Ski

 

7 способов борьбы с проскальзыванием ордеров

Рассмотрите движение без проскальзывания. Читайте про роль угловой и линейной скорости, как действуют поступательное и вращательное движения, формулы.

Задача обучения

• Научиться отличать два разных движения, где качение осуществляется без скольжения.

Что такое проскальзывание?

Проскальзывание (slippage) – это разница между ценой, по которой вы собирались заключить сделку, и ценой, по которой она на самом деле была исполнена.

Допустим, вы видите возможность покупки по цене 1.0607:

Нажимаете кнопку “купить”, но при этом выходит так, что сделка исполнилась по цене 1.0610.

Разница между ценой, по которой мы покупали, и ценой, по которой сделка произошла, составляет 3 пункта. Эти 3 пункта, которые мы потеряли во время открытия позиции, и называются – проскальзыванием.

Проскальзывание может быть как положительным, когда ордер исполняется по более выгодной цене для вас, так и отрицательным, как в примере выше.

Примечательно, что стоп-лоссы и тейк-профиты могут так же проскальзывать и исполняться по цене несколько отличной от той, которую вы задавали при установке приказа.

Отложенные ордера также могут скользить, но при этом они имеют небольшие отличия, но об этом мы поговорим чуть ниже.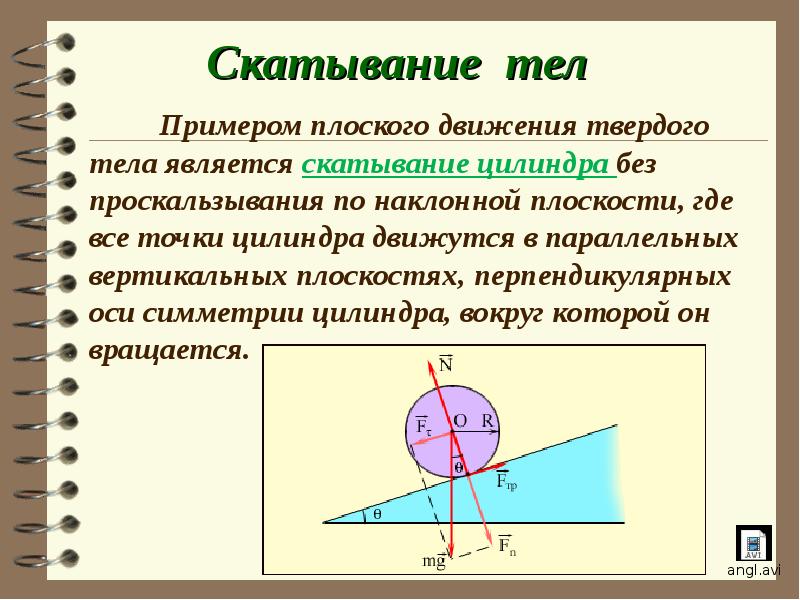

Разница

Теперь давайте попробуем разобраться с понятиями, которые многие очень часто путают и не до конца понимают.

Проскальзывание – это исполнение ордера по цене отличной от цены, указанной вами при установке ордера.

Реквота (requote) – это когда нет цены, по которой вы отправили свой запрос на исполнение ордера.

Представим, что появилось сообщение о новых ценах. Вы нажимаете кнопку покупки, а у вас возникает сообщение, что такой цены уже нет и предложение купить по новой цене. Это и называется реквотой.

С помощью установки параметров проскальзывания при торговле можно избежать реквот.

Основная формула динамики

Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:

F¯ = m*a¯

Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.

В случае движения вращения второй закон Ньютона записывается в виде:

M = I*α

Здесь M и I – моменты силы и инерции, соответственно, α – угловое ускорение.

Проскальзывание – это хорошо или плохо?

Думаю, по ходу чтения статьи у многих возник логичный вопрос: “Проскальзывание – это плохо? Значит ли это, что мой брокер как-то хитрит и делает что-то плохое с моим счётом?”.

Ответ прост.

Наличие проскальзывания – это хорошо, потому что присутствует признак реальности рынка. Это подтверждает, что вы действительно торгуете на межбанке.

Как правило, проскальзывание присутствует на счетах типа ECN. То есть на счетах, которые выводятся на межбанк или выводятся хотя бы частично, что зависит от величины вашей позиции .

Если вы видите проскальзывание, то это не плохо и не хорошо. Это нормально.

Проскальзывание может быть на счетах рыночного типа: ECN, NDD, STP, но при этом оно может присутствовать и на счетах типа Standart.

Наличие проскальзывания – это нормальная ситуация, с которой можно и нужно работать.

Формулы кинематики

Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:

a = Δv/Δt;

v = v0 ± a*t;

S = v0*t ± a*t2/2

Здесь v0 – значение начальной скорости тела, S – пройденный за время t путь вдоль прямолинейной траектории. Знак “+” следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак “-“. Это важный момент.

Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:

α = Δω/Δt;

ω = ω0 ± α*t;

θ = ω0*t ± α*t2/2

Здесь α и ω – угловые ускорение и скорость, соответственно, θ – угол поворота вращающегося тела за время t.

Линейные и угловые характеристики друг с другом связаны формулами:

a = α*r;

v = ω*r

Здесь r – радиус вращения.

Основные пункты

• В качении без скольжения разобраться намного проще, если вы разобьете его на поступательное и вращательное движения.
• Когда объект катится по плоскости без скольжения, то точка контакта между ними не смещается.
• Скорость v скользящего объекта напрямую связана с угловой скоростью ω. Математически выражается как v = ωR, (R – радиус объекта, а v – линейная скорость).

Движение по наклонной плоскости: силы

Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.

Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:

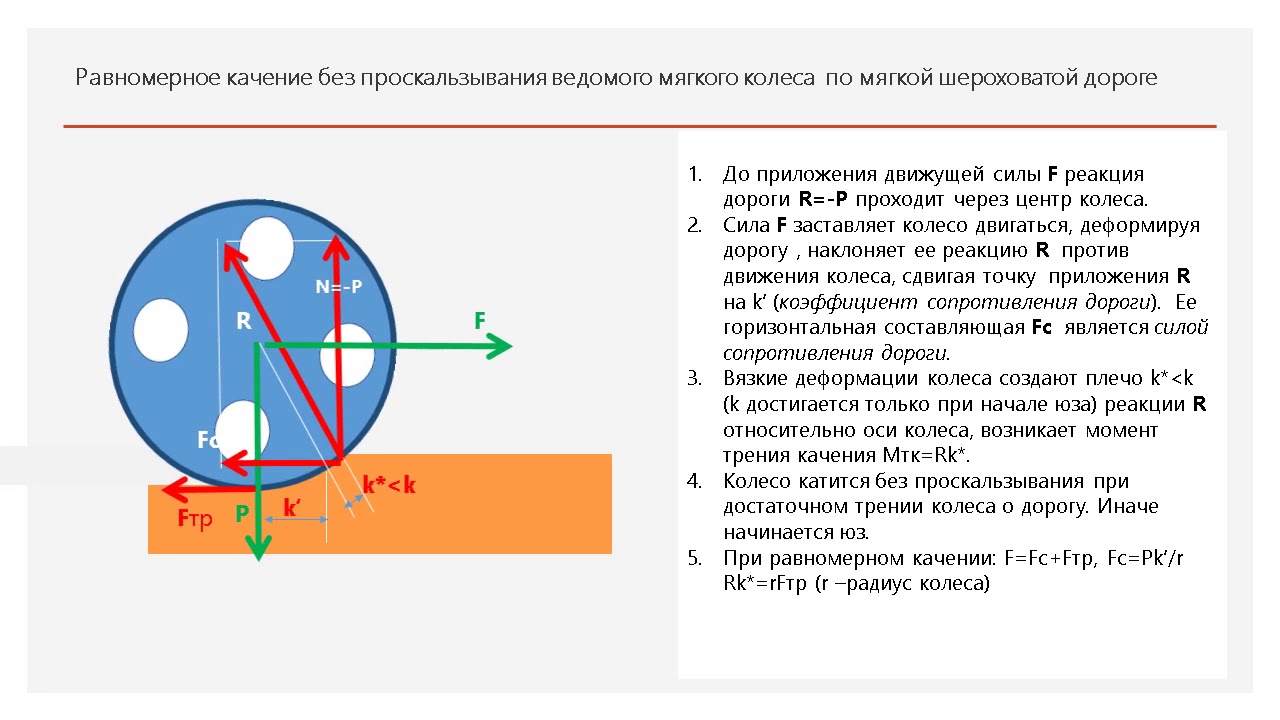
• тяжести;
• реакции опоры;
• трения качения и/или скольжения;
• натяжение нити;
• сила внешней тяги.

Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.

Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.

Проблемы с ликвидностью

Подобное наличие предложение и спроса обозначает присутствие, либо отсутствие ликвидности.

Поэтому первую причину проскальзывания можно обозначить, как Ликвидность.

В данном случае возможны несколько  вариантов.

Представим, что размер ордера больше, чем верхний слой ликвидности. Возможно и то, что осталось очень мало ликвидности, либо у вас был запрошен какой-то очень большой по объему ордер.

Ваш приказ разделяется на части и направляется к нескольким поставщикам ликвидности брокера. В итоге трейдер получает средневзвешенную цену, которая может быть хуже или лучше цены, которую он указал. В такой ситуации ордер проскальзывает частично.

Если поставщик ликвидности присылает отказ исполнения, то возможно  произошла задержка, и ваш приказ отсылался другому поставщику ликвидности. Прошло какое-то время, и рыночное предложение на желаемую вами цену ушло. Как итог, наличие другой цены и соответствующий отказ брокера в исполнении вашего приказа.

Очень часто во время выхода новостей происходит проблема с ликвидностью и ордера сильно скользят.

Почему это происходит? Многие банки и учреждения, которые выступают поставщиками ликвидности, покидают рынок, чтобы обезопасить себя от резких скачков цен и возможных убытков. В это же время расширяются спреды, так как брокеры  хотят обезопасить себя от возможных убытков.

Именно поэтому во время выхода крупных новостей у трейдеров возникают проблемы. Спреды большие, проскальзывания сильные и заработать становится значительно сложнее.

Недостаточная ликвидность, также имеет место при торговле экзотическими валютными парами. К примеру с турецкими лирами, африканскими рэндами, или российскими рублями.

Те, кто торговал во время сильных скачков российской валюты, должны помнить некий период, когда очень многие брокеры просто отключали возможность торговли рублём. Всему причина – отсутствие ликвидности.

Технические Проблемы

Существует ещё одна причина проскальзывания – это Технические проблемы.

К ним относятся сетевые задержки между вашим торговым терминалом и сервером, агрегатором и поставщиками ликвидности, а так же банальная причина – слабый интернет.

В связи с этим хотелось бы рассказать вам про то, что особо крупные дельцы с Wall Street  арендуют здания рядом с центром, чтобы как можно быстрее ордера доходили до торговых серверов, экономя при этом наималейшие доли секунды.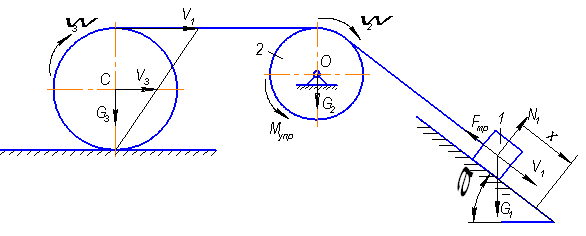

Для нас же вполне будет достаточно иметь быстрый и стабильный интернет. Ведь мы же живём очень далеко от западных серверов. И торговые сервера наших брокеров зачастую находятся за пределами России.

Как бороться с проскальзыванием?

В самом начале хочется сказать важную мысль. Бороться с проскальзыванием не нужно, но нужно с ним работать.

В первую очередь начнём с Технической части. Вам требуется хороший интернет. Помните, что проводное соединение, гораздо лучше и стабильнее, чем тот же Wi-Fi.

Когда начинаем работать в терминале, то стараемся отключать программы, которые используют сеть.

Если вы какой-то мега-скальпер, то для вас это наиболее актуально.  Закрывайте различные программы типа торрентов, вайбера, скайпа, аськи и тому подобных. Нам требуется хорошее соединение, либо нахождение VPS-сервера поближе к вашему брокеру, если вы торгуете с помощью советников.

Если же вы не какой-то мега скальпер, то достаточно иметь хорошее и стабильное подключение к интернету.

Вторым пунктом работы с проскальзыванием стоит отметить Настройки в МТ4.

Когда вы нажимаете на окно нового ордера, в нём есть параметр – “Использовать максимальное отклонение от запрошенной цены”:

Можно выбрать максимальное значение проскальзывания в пунктах, которое будет допускаться. По идее, если цена будет отличаться на большую величину чем установленна в данном параметре, то ордер не исполнится.

К сожалению, на практике это работает не всегда. Связанно это с техническими особенностями серверов брокеров и торговым терминалом Metatrader 4.

Вы должны понять, что данная настройка работает не всегда так, как мы этого хотим.

Аналогично, параметр проскальзывание (slippage) настраивается и в советниках.

Третий пункт – это Использование лимитных отложенных ордеров.

Как мы помним, есть несколько типов отложенных ордеров.

Это Buy stop/Sell stop и Buy limit/Sell limit. Вспомним, что отложенный ордер с окончанием Stop выставляется в расчете на пробой и активацию отложенного приказа, тогда как ордер с окончанием limit, выставляется с целью войти в рынок на откате по лучшей цене. Но существует принципиальная разница в исполнении Stop и limit  ордеров.

При выставленном ордере, допустим Sell stop, он активируется фактически только в момент, когда цена до него дойдёт.

А если же мы выставляем Buy или Sell limit по цене, то ордер заранее отправляется на рынок и у него больше вероятности быть исполненным именно по той цене, которую мы указали.

Таким образом, ордера типа limit бронируют для нас определённую часть ликвидности,  но при условии, что у вас тип счёта с выводом на межбанк.

Конечно, даже подобные ордера могут проскальзывать, но вероятность этого намного меньше, чем у рыночных и stop ордеров.

Четвёртый пункт – Торговля на высоких таймфреймах.

Если вы торгуете на таймфрейме М5, то проскальзывание в 1 пункт для вас заметно, но если же вы торгуете на дневных графиках, то проскальзывание в 5 пунктов какой-то большой погоды для вас не делает.

Поэтому можно с проблемой бороться, а можно просто исключить её и сделать несущественной, перейдя на более высокий таймфрейм.

Пятый пункт – Не торговать на новостях.

Я уже неоднократно упоминал, что проблема с ликвидностью возникает, как правило, на выходе различных новостей. Это и экономические данные, речи политиков и так далее.

Поэтому примерно за полчаса перед выходом новости и полчаса после её выхода мы стараемся не торговать. Так мы исключаем проблему с ликвидностью.

Шестой пункт –  Сменить тип счёта/брокера.

Конечно, можно заменить своего брокера или изменить тип своего счёта, но если говорить честно, то это погоня за какой-то неосуществимой мечтой. И к тому же это обычно перекладывание ответственности за потери с себя любимого на брокера, исполнение, маркет-мейкеров, злодейку судьбу и так далее.

Поэтому к этому пункту стоит подходить со здравым умом и определенной долей скептицизма. Потому что если вы начнёте менять брокеров, типы счетов, то это может затянуться надолго и ни к чему,  как правило, хорошему не приводит.

Седьмой пункт – Фильтр по волатильности.

Представим, что вы любите торговать активный рынок. Вы знаете, что среднее проскальзывание во время выхода новостей 10 пунктов. А средняя прибыль по таким сделкам у вас – 30 пунктов.  Получается, что проскальзывание забирает у вас примерно 30% прибыли.

Допустим, вы торгуете часть новостей, но при этом знаете, что одни новости дают среднее движение в 30 пунктов, а другие дают среднее движение 60 пунктов.

Если вы будете брать сделки со средним движением в 60 пунктов, то проскальзывание будет съедать не 30%, а всего 17%.

Таким образом, используя новости только с высокой волатильностью, вы сможете снизить ущерб, наносимый вашей прибыли.

Аналогично, если вы знаете, что среднее проскальзывание при активном рынке, но без новостей 2 пункта. В этом случае можно торговать только в те дни, когда волатильность повышена, чтобы увеличить профит и уменьшить убытки, полученные от проскальзывания.

ИССЛЕДОВАНИЕ ДВИЖЕНИЯ ТРЕХЗВЕННОГО ПОЛЗАЮЩЕГО РОБОТА ПО НЕДЕТЕРМИНИРОВАННОЙ ПОВЕРХНОСТИ | Яцун

1. Li G., Zhang H., Zhang J., Bye R. T. Development of Adaptive Locomotion of a Caterpillar-Like Robot Based on a Sensory Feedback CPG Model // Advanced Robotics. 2014. V. 28. № 6. P. 389-401.

2. Matsuo T., Ishii K. Adaptative Motion Control System of a Snake-Like Robot Using a Neural Oscillator Netowork // 2014 Joint 7th Int. Conf. on Soft Computing and Intelligent Systems (SCIS) and 15th Int. Symposium on Advanced Intelligent Systems (ISIS), Kitakyushu, Japan. 2014.

3. Conkur E. S., Gurbuz R. Path Planning Algorithm For Snake-Like Robots // Information Technology And Control. 2008. Vol. 37. № 2. P. 159-162.

4. Ворочаева Л.Ю., Наумов Г.С., Яцун С.Ф. Моделирование движения трехзвенного робота с управляемыми силами трения по горизонтальной шероховатой поверхности // Изв.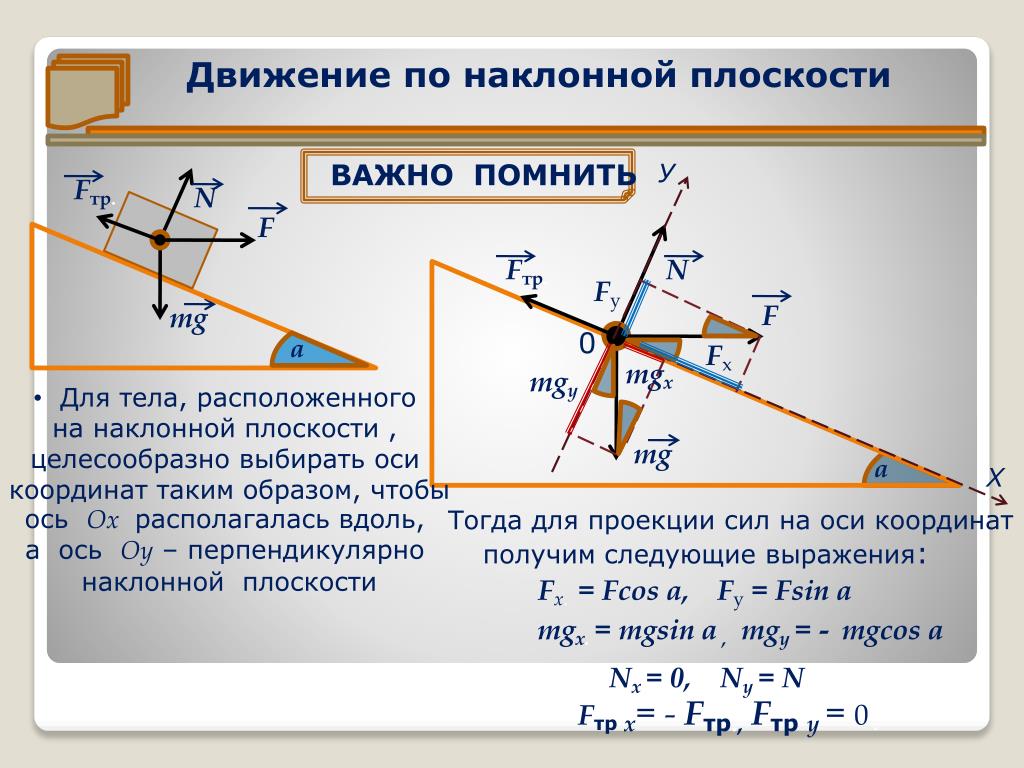 РАН. ТиСУ. 2015. № 1. С. 156-170.

5. Ворочаева Л.Ю., Яцун А.С., Яцун С.Ф. Моделирование движения пятизвенного ползающего робота с управляемым трением по поверхности с препятствиями // Изв. РАН. ТиСУ. 2017. № 3. С. 191-216.

6. Яцун С.Ф., Мальчиков А.В., Жакин А.И. Динамические опорные элементы ползающих роботов для движения по наклонным поверхностям // Известия Юго-Западного государственного университета. 2012. №2 (41). С.89-95.

7. Jatsun S.F., Volkova L.Yu., Naumov G.S., Yatsun A.S. Modelling of movement of the three-link robot with operated friction forces on the horizontal surface // 16th Intern. Conf. on Climbing and Walking Robots and the Support Technologies for Mobile Machines. Sydney, Australia, 2013. P. 677-684.

8. Jatsun S., Vorochaeva L., Yatsun A., Savin S., Malchikov A. Bio-inspired adaptive control strategy for a snake-like robot // 19th Intern. Conf. on System Theory, Control and Computing (ICSTCC), Cheile Gradistei — Fundata. Romania, 2015. P. 273-278.

9. Jatsun S.F., Vorochaeva L.Yu., Yatsun A.S., Savin S.I. Study of Caterpillar-like Motion of a Four-link Robot // 14th IFToMM World Congress. Taipei, Taiwan. 2015. P. 1-6.

10. Jatsun S., Vorochaeva L., Yatsun A., Malchikov A. Theoretical and Experimental Studies of Transverse Dimensional Gait of Five-Link Mobile Robot on Rough Surface // 10th Intern. Symposium on Mechatronics and its Applications ISMA, Sharjah, UAE, 2015. P. 1-6.

11. Jatsun S.F., Loktionova O.G., Vorochaeva L.Yu. Modeling of the operated movement to a caterpillar of the similar robot on a horizontal surface // Intern. J. of Pharmacy & Technology. 2016. Vol. 8 (3). P. 15231-15239.

Toyota Land Cruiser Prado: Когда дизайн не важен

В Toyota Motor грядут революционные изменения в области дизайна. Раньше внешний вид моделей утверждал так называемый комитет, в который входило 100 человек. В основном это были технари и боссы разного уровня, каждый из которых вносил правку и замечания, наподобие – «Такой изгиб крыла не пройдет, с технической точки зрения будет затратно» или «Стиль слишком дерзкий, не в духе традиций компании». Учитывая преобладание консервативных взглядов в Toyota, неудивительно было наблюдать на выходе довольно серенькие внешне серийные автомобили. Но увидев, во что превратил Кia главный дизайнер марки Питер Шрайер, президент Toyota Акио Тойода решил: «Мы больше не будем делать скучные машины!» Комитет сократили до 10 человек, и творческие идеи пошли в жизнь.

По холоду в России

Революция в дизайне пока миновала Land Cruiser Prado.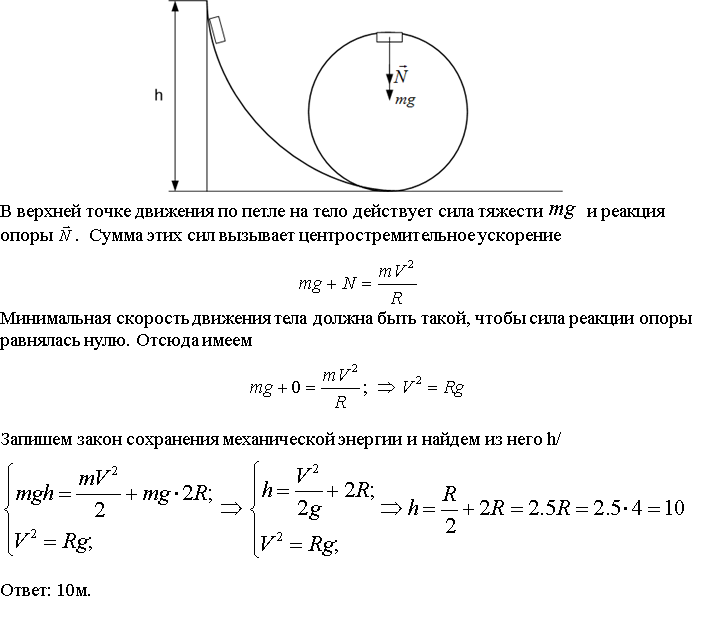 Это было очевидно по двум стоявшим рядом внедорожникам – обновленному и предшественнику – в московском пресс-парке Toyota, куда я приехал забрать автомобиль. По сути, Prado – та же модель образца 2009 г., облик которой создала европейская команда Toyota с участием российского дизайнера Владимира Пирожкова. Но передок машины изменили: исчезли плаксивые фары, которые делали лицо Prado скучным, поставили новую решетку радиатора, капот сделали в стиле старшего Land Cruiser 200, задние фонари сохранили форму, но стали светодиодными. Новый бампер удлинил внедорожник на 60 мм. В салоне – новые руль, приборы и центральная консоль с блекловатым 8-дюймовым сенсорным экраном в обрамлении опять же скучного серебристого пластика. Под дисплеем для управления внедорожными настройками появились две «шайбы» (вместо одной большой), меняющие режимы демультипликатора коробки передач и системы выбора режима движения по бездорожью Multi Terrain Select (MTS).

Пятиместная версия Prado теперь может оснащаться раздельным климат-контролем и подогревом сидений заднего ряда (раньше только семиместная). Вариант с проверенным временем 177-сильным дизелем 2,8 л и 6-скоростной автоматической коробкой передач – то, что надо для дальней поездки к промерзшему полигону под Минском. Ночной бросок на 1000 км вчетвером с забитым багажником оказался неутомительным для всех пассажиров: те, кто сзади, теперь тоже могут регулировать наклон спинки сидения. У одного из них даже получилось выспаться, что, по его признанию, в машине с ним бывает очень редко. За комфорт пассажирам нужно также благодарить установленные сзади пневмоподвеску и систему KDSS, контролирующую работу стабилизаторов поперечной устойчивости. В системе настроек режимов движения прибавились Sport S и Sport S+ (прежде были Eco, Normal и Sport), но я использовал экономичный как самый комфортный. Расход вышел 8,7 л при умеренных, до 100 км/ч, скоростях на трассе и 10 градусах мороза за бортом.

Порадовало еще одно техническое новшество в Prado – автоматическое переключение с дальнего на ближний свет. Система срабатывала всегда четко и вовремя, не ослепляя ни встречный, ни попутный транспорт, но не реагировала на отражение от дорожных знаков. Там, где была видна дорожная разметка, надежно срабатывала система контроля полосы движения. Но она помогала водителю только предупреждающим звуком – к сожалению, старомодный гидроусилитель руля Prado держать машину в полосе, как электроусилители, не может.

Движение по шоссе вообще не самая сильная сторона внедорожников – со скоростью высоким машинам лучше не шутить. И Prado здесь не исключение, хотя у него установлены адаптивные амортизаторы AVS (меняют жесткость отбоя подвески) и активные стабилизаторы (упомянутая KDSS). Но он и не провоцирует на быструю езду – в Prado приятно спокойно парить над дорогой, а не закладывать виражи или резко ускоряться. К тому же он прожорлив: если включать удобные для обгона режимы Sport S или Sport S+, расход топлива вырастает чуть ли не в 2 раза.

Дорога от шоссе на армейский полигон, где Prado ждали заснеженные овраги, канавы, крутые спуски и подъемы, была накатана шестиосным армейским колесным тягачом. Ледяной каток позволил убедиться, что система стабилизации движения Prado работает отменно. Я хулиганил газом и рулем, пытаясь сорвать машину в занос, но тщетно. На скорости до 60 км/ч электронные помощники держали машину в узде. Азарт пришлось придержать до настоящего бездорожья, где ESP можно отключить (но после 50 км/ч она вновь активируется автоматикой).

Внедорожный арсенал у Prado на высоте: постоянный полный привод с понижающим рядом передач (демультипликатором), принудительная блокировка центрального и заднего дифференциалов. Вдобавок короткие свесы, высокий клиренс 215 мм и запас хода подвесок (гидравлика KDSS регулирует жесткость опор стабилизаторов поперечной устойчивости, а на бездорожье полностью распускает их, делая ходы колес максимальными). И плюс вспомогательная электроника. Когда я вывесил заднее колесо, автомобиль забуксовал, и демультипликатор, конечно, не помог. Выручила MTS. В ней пять режимов – «Грязь и песок» (Mud & Sand), «Щебень» (Loose Rock), «Могул» (Mogul, т. е. бугры и рытвины), «Камни и грязь» (Rock & Dirt), «Крупные камни» (Rock). В каждом из режимов изменяется алгоритм управления дроссельной заслонкой, тормозной и антипробуксовочной системами для оптимального распределения крутящего момента по колесам и обеспечения максимальной тяги на разных покрытиях. В обновленной версии появился режим Auto, который анализирует информацию с датчиков и подбирает оптимальный режим, освобождая от раздумий, что же лучше выбрать на снегу – «Грязь и песок» или «Камни и грязь»? Включив Auto, я выехал из канавы без проблем – отличный помощник!

Съехав в небольшой овраг, я пытался использовать круиз-контроль для бездорожья Crawl Control. Он держит маленькую скорость (от 2 до 10 км/ч), позволяя водителю управлять машиной, не трогая педали. Но с ним я на полигоне общего языка так и не нашел. Многие подъемы в карьере приходилось преодолевать ходом, и «пешеходный круиз» только мешал.

По жаре в Африке

15 часов полета, две пересадки, и мы попадаем в сказку. В Намибии нас ждали разные ландшафты – пустыня, горы, камни, песок и лесные заросли. За три дня мы накатали на Prado около 800 км. Немного, если отмерять по обычным дорогам, но по ним мы почти не ездили. Дорог в Намибии проложено сравнительно много – 60 000 км, но только десятая их часть с асфальтовым покрытием, остальное – грунтовки.

В Намибии левостороннее движение, но у нас были леворульные европейские версии, управлять которыми континентальным европейцам было привычнее и безопаснее. По грунтовым дорогам мы двигались колонной. Машины были оснащены тем же дизелем 177 л. с., но в салоне бросилось в глаза отсутствие кнопки принудительной блокировки заднего дифференциала (в европейской версии в заднем мосту стоит дифференциал повышенного трения Torsen) и блока подогревов (руля, лобового стекла, форсунок омывателя, предпускового мотора), которые были у московского Prado, – да и зачем они, когда за бортом +35 градусов Цельсия?

Маршрут начинался от портового городка Уолфиш-Бей на побережье Атлантического океана. Мы то углублялись внутрь страны, то возвращались обратно к берегу.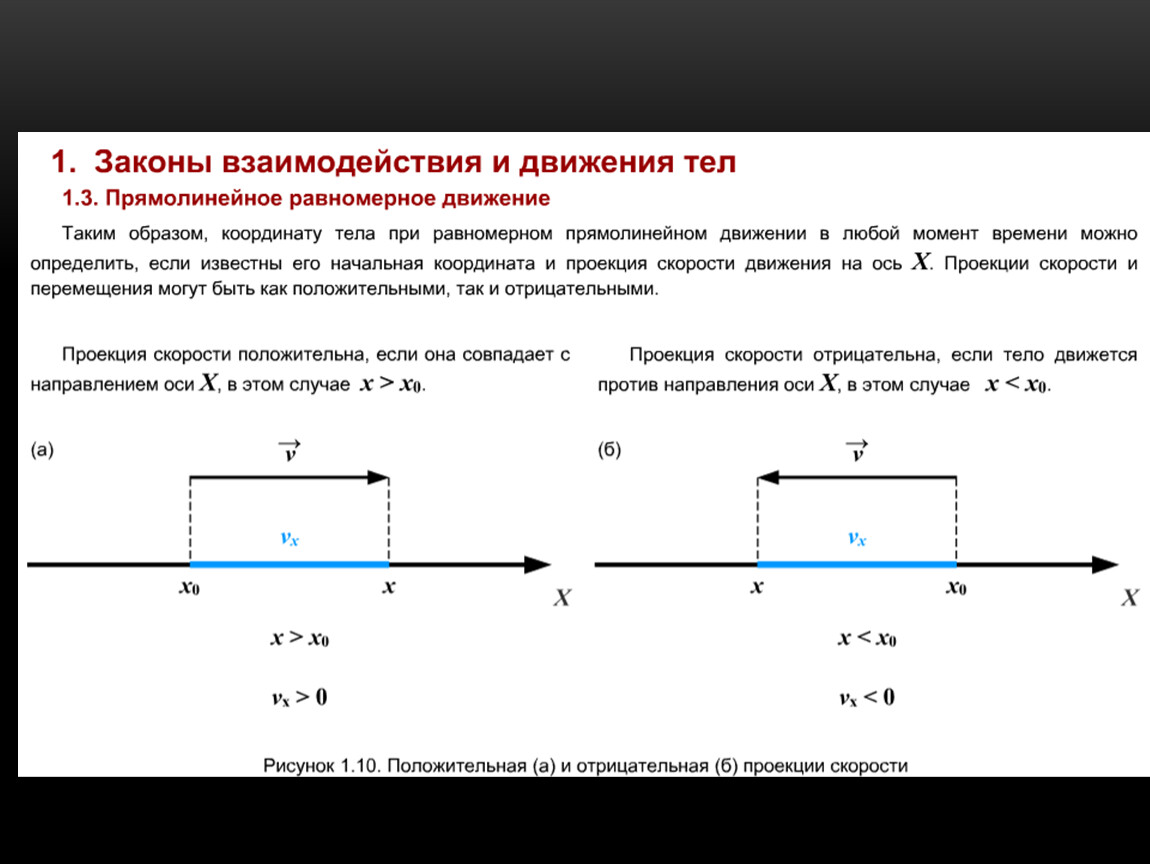 Несмотря на огромные просторы, значительная часть Намибии – пустыни Калахари и Намиб, и всего треть страны пригодна для жизни людей. Но на эту треть мы почти не заезжали. Песчаные пляжи и пустыни – самое легкое, что было на пути: давление в колесах скидывали с 2,5 до 1,5 атмосфер, и мы летели по песку, часто даже не включая демультипликатор.

Монотонная саванна, в которой нас встречали, а иногда сопровождали обезьяны, буйволы, коровы и страусы, быстро кончилась. Примерно через 100 км чередования гор и пустынь, причем разного цвета – то светло-желтого, то серого, то цвета кабачковой икры, – и появился первый лесной участок. Там были обед и привал, сопровождавшийся строгим предупреждением не разбредаться: вокруг дикие животные, а они тоже есть хотят. Чтобы избавить нас от местной мошкары, подожгли находившийся вокруг в изобилии слоновий помет и пожелали всем приятного аппетита.

После ланча, не успели мы отъехать и километра от места стоянки, из леса наперерез нам вышел производитель репеллента – слон, вернее, слониха. «Из машины не выходить!» – скомандовал наш руководитель. Честно говоря, особого желания покидать Prado и так не было. Явление было настолько впечатляющим, что, когда мы остановились на ночлег неподалеку в палатках, многие не на шутку беспокоились, не затопчут ли нас слоны ночью.

На камнях и в болоте

В начавшейся вскоре гористой местности пришлось задействовать весь потенциал Prado. Наверняка вам когда-нибудь приходилось ходить в горах по крутому склону, перепрыгивая с камня на камень. То же самое делали мы, но на машине. Понижающий ряд, MTS в «каменный» режим – то «Крупные камни», то «Щебень». Иногда я включал и Auto Mode, и он тоже не подводил. Спуски, подъемы – и все по камням. Я вышел из машины, чтобы сделать пару кадров, и едва не подвернул ногу – здесь идти-то невозможно, а мы едем!

Пока фотографировал, а затем аккуратно, чтобы не убиться, перепрыгивал по валунам до машины, остальные скрылись за перекатом. Мы добрались на Prado до вершины и замерли. Колонна ушла, вернее – уползла вперед, и нашему взору открылся пейзаж в виде непроходимых каменистых россыпей – что на спуске, что на подъеме. А главное – куда ехать? Ведь это же не песок, где остаются следы от впереди идущего автомобиля. Да и понятие «ехать» разум воспринимал с трудом. Движение в любом направлении выглядело безумием. Мой напарник, поклонник марки Toyota, впервые приглашенный на такое мероприятие компанией, наотрез отказался садиться за руль: «Разве здесь может проехать автомобиль?!»

Кое-как мы вычислили верное направление и двинулись вперед. И скажу честно, в этот момент мне было все равно, какой у центральной консоли Prado дизайн, пластик и экран. Жизненно важными были внедорожные способности машины. Здесь нам пригодился бесполезный в российских снегах режим Crawl Control. На каменной горе, когда каждое неверное движение газом может закончиться переворотом автомобиля, Crawl вычислял оптимальный ритм движения с минимальным проскальзыванием колес, и Prado медленно сползал вниз и так же плавно карабкался вверх, позволяя водителю концентрировать внимание на руле и дороге. Можно было вручную подстраивать скорость движения (пять ступеней), но лучше электроники справляться не удавалось.

Кстати, в обновленном Prado появились камеры кругового обзора. Особой пользы, кроме удобства при парковке, я в этой функции поначалу не заметил. Так, преодолевая подъем, когда капот закрывал нужный сектор обзора, огромные камни на картинке с передней камеры выглядели как пляжная галька – полезной информации никакой. Но чуть позже, когда нам пришлось проезжать сквозь тесные ворота, причудливо выложенные природой слоеным пирогом из камней, я мог ориентироваться только по изображению на камере с контурами габаритов машины. Без нее мы исцарапали бы все бока Prado.

Crawl Control оказался хорош как в горах, так и для преодоления заболоченных ущелий, где нога погружалась в слой раскисшей почвы почти по колено. Пробиться ходом здесь не удавалось – лихачи зависали на брюхе. Их терпеливо вытягивала лебедкой Toyota Hilux службы сопровождения, а за процессом с окружающих скал с любопытством наблюдали крупные обезьяны. А вот с включенным «внедорожным круизом» никаких сложностей на мокром участке не возникало – почти не буксуя, Prado уверенно проползал низину.

И такое веселье продолжалось почти три дня. Вероятно, создатели машины проделали немало подобных маршей, потому почти неудивительно, что, даже болтаясь по валунам, Prado продолжал радовать комфортом. Мягкие вставки по бокам центральной консоли избавили нас от синяков на ногах, удобная посадка в креслах и ручки на передних и средних стойках кузова помогали при качке и кренах, огромный ящик под широким центральным подлокотником хранил бутылки с водой в прохладе, а климат-контроль спасал от жары нас самих. Вода, между прочим, в Намибии вообще в дефиците – проще купить Coca-Cola, чем питьевую воду.

В таких суровых условиях, на выживание, у Prado найдется мало соперников, и эту уникальную ДНК обещают сохранить в нем надолго, несмотря на все дизайнерские революции. Скорее всего, в новом поколении облик модели изменится, но основа – высокие внедорожные способности, надежность и качество – останутся прежними.

Тест-драйв организован компанией Toyota Motor.

Stick Slip Motion — обзор

8.1 Введение

Скрип и дребезжание — это общая терминология, используемая в автомобильной промышленности для описания кратковременных переходных шумов, которые генерируются относительным движением или ударами между частями автомобиля. Скрип относится к скачкообразным движениям между частями, находящимися в фрикционном контакте, в то время как скрежет относится к ударам между частями, которые обычно находятся в свободном контакте. Возникновение этих звуков часто зависит от правильного набора условий эксплуатации транспортного средства при работе двигателя / трансмиссии с возбуждением от поверхности дороги или от возбуждения ветра при высоких скоростях транспортного средства.Эти звуки непостоянны и непродолжительны. Они раздражают уши по сравнению с другими непреходящими источниками шума, такими как шум ветра, трансмиссии и дороги. Писк и дребезжание — это нежелательные шумы, не связанные с какой-либо полезной работой автомобиля. Помимо проблем с долговечностью продукта, это также воспринимается потребителями как недостаток качества и обозначается как TGW (что-то идет не так) в автомобильной промышленности. К тому же скрип и дребезжание влечет за собой огромные гарантийные расходы на продукцию.Это делает писк и дребезжание одной из самых важных и сложных тем, изучаемых академическими кругами и промышленностью. В прошлом усилия были сосредоточены на методах «поиска и исправления», применяемых к серийным автомобилям или близким к производству прототипам на поздних стадиях разработки продукта. В результате большинство корректирующих действий — это временные решения из-за ограничения замораживания инструмента. Это также связано с проблемами качества при большом пробеге.

Традиционные методы поиска и устранения проблем со скрипом и дребезжанием основаны на субъективной оценке при выявлении и локализации события до принятия корректирующих действий.Практически отсутствовали аналитические инструменты для заблаговременной профилактики. Динамика писка включает в себя сложное залипание и проскальзывание, очень нелинейное явление, поэтому рассматривались только нелинейные инструменты CAE, такие как ADAMS, DADS DYNA-3D или ABACUS. Ключ к успеху заключается в создании сложных контактных элементов, полностью имитирующих динамическое поведение контакта. Теоретически это достижимо, но на практике оно ограничено размером метрики и вычислительными возможностями современных компьютеров.На сегодняшний день многие эксперты CAE все еще работают над фундаментальным моделированием «вывод на диск» и еще не пришли к выводу. Что касается моделирования дребезжания, оно включает в себя сложное периодическое нелинейное воздействие и требует специальной нелинейной модели CAE для прямого моделирования этих явлений. Анализ методом конечных элементов почти всегда используется при анализе вибрационной динамики этих систем, хотя полная нелинейность проблемы с переходными ударами не учитывается в анализе.Очень сложно, если не невозможно, использовать инструмент CAE в нелинейном моделировании дребезжания для крупномасштабной модели транспортного средства.

Гибридный подход был разработан Hsieh et al. в 1997 г. [1], в котором резонансные частоты и формы колебаний из линейной модели конечных элементов используются для описания локальной динамики ударных компонентов в терминах простой модели массы пружины с множеством степеней свободы, которая также может учитывать локальная нелинейная динамика удара. Модель будет реализована в программном обеспечении для анализа динамики множества тел.Однако этот подход не включает прогнозы излучаемого шума из-за ударов. Этот метод был применен для решения проблем на уровне компонентов, таких как проблема дребезжания перчаточного ящика.

Следовательно, очевидно, что для предотвращения дребезжания необходим упрощенный инструмент CAE, чтобы можно было заранее внести изменения в конструкцию для предотвращения потенциальных проблем с дребезжанием. Линейная модель конечных элементов всего транспортного средства использовалась для расчета резонансных частот для мод колебаний более низкого порядка в качестве основы для определения горячих точек дребезжания.Области с большими амплитудами относительного движения на определенных частотах возбуждения при анализе частотной характеристики идентифицируются как горячие точки, где наиболее вероятно возникновение дребезжания. Амплитуда относительных движений для линейной модели используется для масштабирования интенсивности дребезжания для конкретного профиля возбуждения.

За годы исследований первопричин было обнаружено, что скорость контакта определяет уровень излучаемого звука, вызванного дребезжанием [2]. Связь между контактной скоростью и излучаемым звуком в ближней зоне для типичного случая дребезжания, наблюдаемого в транспортном средстве, была установлена ​​путем накопления экспериментальных данных.Смысл этого открытия заключается в том, что скорость контакта может служить показателем для количественной оценки степени дребезжания и использоваться для установления критерия дребезжания. Более того, с точки зрения разработки транспортного средства, наиболее важной задачей является прогнозирование возникновения дребезжания и количественная оценка его серьезности. Другими словами, проверка возможных проблем с дребезжанием более практична, чем моделирование нелинейной динамики удара для автомобильной промышленности.

Соответственно, инструмент CAE, названный Rattle HotSpot Check (RHSC), был разработан для предотвращения дребезжания.Для разработки моделей не требуется фактическое транспортное средство, и она может продолжаться на ранней стадии процесса разработки транспортного средства, так что, когда будут доступны прототипы транспортных средств, тестирование для выявления и подтверждения фактического возникновения дребезжания может продолжаться эффективно и результативно. По мере накопления опыта работы с инструментом CAE можно предложить модификации конструкции до того, как будут созданы реальные прототипы, с уверенностью, что потенциальная проблема с грохотом устранена.

Основная идея этого инструмента состоит в том, чтобы найти место, где две части проникают друг в друга при линейном гармоническом движении, а затем оценить соответствующую скорость контакта, чтобы получить показатель дребезжания.На основе эмпирических данных была установлена ​​связь между линейной и нелинейной контактной скоростью. Таким образом, нелинейное явление ударного контакта было упрощено линейной аналогией. Следовательно, был разработан алгоритм быстрой проверки контактов, который использует линейную модель конечных элементов и результаты анализа, но сохраняет лежащую в основе физику контакта. Это также позволяет интегрировать RHSC в текущую практику NVH CAE путем последующей обработки стандартных результатов NVH CAE для определения местоположения дребезжания, вызванного возбуждением транспортного средства.Простая задача сравнительного анализа используется для иллюстрации концепции и алгоритма инструмента, а также для демонстрации точности числовой схемы, используемой инструментом. Корреляция CAE / тестовых примеров транспортных средств включена, чтобы показать достоверность прогнозов, полученных с помощью RHSC. Показаны несколько программных приложений для транспортных средств, чтобы продемонстрировать возможности и типичное использование этого инструмента. Основа для применения инструмента RHSC также включена для подготовки пользователей.

Движение скольжения и устойчивость упругой системы с одной степенью свободы с трением, зависящим от скорости и состояния

Мы рассматриваем квазистатическое движение и устойчивость упругой системы с одной степенью свободы, испытывающей фрикционное скольжение.Система представлена ​​блоком (ползуном), скользящим со скоростью V и соединенным пружиной с жесткостью k с точкой, в которой движение осуществляется со скоростью V ₀ Мы принимаем определяющую силу трения, зависящую от скорости и состояния. соотношения для ползунка, которые приблизительно описывают экспериментальные результаты Дитериха и Руина в диапазоне скоростей скольжения V . В простейшем отношении напряжение трения аддитивно зависит от члена A In V и переменной состояния θ; переменная состояния θ эволюционирует с характерным расстоянием скольжения до значения — B В V , где предполагается, что константы A, B удовлетворяют B > A > 0.Ограниченные результаты представлены на основе аналогичного закона трения с использованием двух переменных состояния.

Линеаризованный анализ устойчивости прогнозирует движение с постоянной скоростью скольжения при V ₀ для перехода от стабильного к нестабильному при уменьшении жесткости пружины k ниже критического значения k _cr . При нейтральной устойчивости прогнозируются колебания скорости скольжения. Приведенный здесь нелинейный анализ движений скольжения использует технику бифуркаций Хопфа, прямое определение траекторий фазовой плоскости, методы Ляпунова и численное интегрирование уравнений движения.Небольшие, но конечные циклы ограничения амплитуды существуют для одного значения k , если используется одна переменная состояния. С двумя переменными состояния существуют колебания в небольшом диапазоне k , которые претерпевают удвоение периода и затем приводят к очевидно хаотическим движениям при уменьшении k .

Возмущения от установившегося скольжения вызываются ступенчатым изменением движения точки приложенной нагрузки. Рассмотрены три случая: (1) скорость точки нагрузки V ₀ внезапно увеличивается; (2) точка нагрузки останавливается на некоторое время, а затем снова перемещается с постоянной скоростью; и (3) смещение точки нагружения внезапно увеличивается, а затем останавливается.Во всех случаях для всех значений k : достаточно большие возмущения приводят к неустойчивости. Основные выводы: (1) неустойчивость «прерывистого скольжения» возможна в системах, для которых устойчивое скольжение является стабильным, и (2) физическое проявление квазистатических колебаний чувствительно к свойствам материала, жесткости, а также природе и величине возмущений нагрузки.

Что такое прерывистое скольжение?

Прерывистое скольжение, также называемое «заеданием», — это проклятие инженеров и машиностроителей, которым требуется плавное и точное движение.Проще говоря, это рывки, от которых страдают как подшипники скольжения, так и подшипники скольжения с рециркуляцией при переходе из состояния покоя в движение. Вот почему происходит прерывистое скольжение…

Когда два объекта скользят друг относительно друга, трение препятствует их движению. Но есть два типа трения: статическое (также называемое отрывом) и кинетическое (также называемое динамическим). Трение — это липкое (каламбурное) явление, которое нужно определить и измерить, но на фундаментальном уровне статическое трение вызывается молекулярной связью, которая возникает, когда две поверхности находятся в контакте.Кинетическое трение в первую очередь вызвано шероховатостью поверхности, которая препятствует движению двух тел относительно друг друга.

Статическое трение увеличивается со временем контакта. Другими словами, чем дольше две поверхности контактируют в состоянии покоя (не движутся), тем выше будет их статическое трение. Было обнаружено, что кинетическое трение в основном постоянное независимо от скорости, хотя некоторые изменения могут происходить при очень малых скоростях. (Скорость поверхностей определяет, как долго любые две области на поверхностях находятся в контакте друг с другом.)

Взаимосвязь между трением и скоростью для смазываемых поверхностей (как и в случае подшипников с рециркуляцией) показана на кривой Штрибека. Толщина смазочной пленки является важным параметром трения, и подшипники могут работать в трех областях смазки:

• Граничная смазка — где трение определяется свойствами поверхности
• Смешанная смазка — где трение зависит как от свойств поверхности, так и от свойств смазки, а также от скорости.
• Гидродинамическая смазка — где трение определяется вязкостью смазочной пленки.

Изображение предоставлено: природа.com

Поскольку линейное движение не является непрерывным — в отличие от радиальных подшипников, линейные подшипники должны останавливаться на конце направляющей и возвращаться в обратном направлении — линейные рециркуляционные подшипники проводят больше времени в зоне смешанной смазки, что делает их подверженными заеданию -соскальзывать.

В подшипниках с рециркуляцией, начало движения втягивает смазку в зону контакта между двумя поверхностями, уменьшая контакт поверхности с поверхностью и вызывая падение сил трения. По мере увеличения скорости смазочная пленка увеличивается, а трение уменьшается.Но после определенного момента трение на самом деле увеличивается и вызывает вязкое сопротивление. Вот почему важно использовать смазку подходящего типа и количество смазки для рециркуляционных подшипников.

В подшипниках скольжения прерывистое скольжение также может быть проблемой из-за более высокого коэффициента трения контакта скольжения (а не качения). Чтобы свести к минимуму прерывистое скольжение при использовании линейных подшипников скольжения, важно обеспечить правильное расположение подшипников в соответствии с правилом 2: 1 или соотношением 2: 1.

Переход, который происходит при инициировании движения, от более высокого статического трения к более низкому динамическому трению, может привести к превышению системой целевого положения и отрицательно повлиять на точность позиционирования. Но эффекты прерывистого скольжения можно свести к минимуму за счет правильной конструкции систем подшипников скольжения и надлежащей смазки рециркулирующих подшипников.

Изображение предоставлено доктором Джеймсом Хедбергом, CUNY

Влияние смачиваемости частиц на скачкообразное движение контактной линии

Динамика линии контакта имеет решающее значение при определении характера осаждения испаряющихся коллоидных капель.Используя высокоскоростную интерферометрию, мы непосредственно наблюдаем скачкообразное движение контактной линии in situ и можем определить мгновенную форму испаряющихся пиколитровых капель, напечатанных струйной печатью, содержащих наночастицы различной смачиваемости. Интегрированная с посмертная оптическая профилометрия образцов осаждения , может быть определена мгновенная объемная доля частиц и, следовательно, скорость осаждения частиц. Результаты показывают, что скачкообразное движение контактной линии сильно зависит от смачиваемости частиц.В то время как скачкообразное движение наблюдается для наночастиц, которые менее гидрофильны (, т. Е. , угол контакта частиц θ, ≈ 74 ° на границе раздела вода-воздух), что приводит к осаждению нескольких колец, непрерывному удалению линии контакта наблюдается для более гидрофильных наночастиц (, т. е. , θ, ≈ 34 °), что оставляет структуру с одним кольцом. Модель разработана для прогнозирования количества частиц, необходимых для закрепления линии контакта, на основе баланса сил гидродинамического сопротивления, межчастичного взаимодействия и поверхностного натяжения, действующего на частицы вблизи линии контакта с различной смачиваемостью частиц.Прогнозируется трехкратное увеличение количества частиц, необходимых для закрепления, когда смачиваемость частиц увеличивается от угла смачивания θ ≈ 74 ° до θ ≈ 34 °. Это открытие объясняет, почему частицы с большей смачиваемостью образуют структуру с одним кольцом, а частицы с более низкой смачиваемостью образуют структуру с несколькими кольцами. Кроме того, обнаружено, что скорость осаждения частиц зависит от смачиваемости частиц и изменяется со временем.

У вас есть доступ к этой статье

Подождите, пока мы загрузим ваш контент… Что-то пошло не так. Попробуй еще раз?

Прилип-скольжение в квантовом поле

Марк И. Дикман
• Департамент физики и астрономии, Мичиганский государственный университет, Ист-Лансинг, штат Мичиган, 48824, США

16 мая 2016 г. & bullet; Physics 9, 54

Электронный кристалл, скользящий по жидкому гелию, демонстрирует качественно новый тип скачкообразного движения, возникающего в результате взаимодействия электронов с квантовым полем.

Рисунок 1: Кристалл Вигнера из электронов (зеленые сферы) вынужден скользить по поверхности жидкого гелия под действием напряжения, которое прикладывается между двумя погруженными в воду металлическими пластинами (желтые полосы). Рис и его коллеги наблюдали, что скорость кристалла демонстрирует тип скачкообразного движения, когда напряжение линейно нарастает во времени. Вигнеровский кристалл электронов (зеленые сферы) вынужден скользить по поверхности жидкого гелия под действием напряжения. , который наносится между двумя погруженными в воду металлическими пластинами (желтыми полосами).Рис и его коллеги заметили, что скорость кристалла показывает … Показать больше Рисунок 1: Вигнеровский кристалл электронов (зеленые сферы) вынужден скользить по поверхности жидкого гелия под действием напряжения, которое прикладывается между две погруженные металлические пластины (желтые полосы). Рис и его коллеги заметили, что скорость кристалла демонстрирует тип скачкообразного движения по мере линейного увеличения напряжения во времени. ×

Электроны, парящие в свободном пространстве на несколько нанометров над поверхностью жидкого гелия, составляют один из самых идеальных 2D-системы, которые ученые могут создавать в лаборатории (рис.1). Поскольку она не имеет дефектов, эта система обеспечивает уникальную платформу для изучения явлений многих тел, которым не препятствует беспорядок, присущий другим системам конденсированного состояния. Интересным примером является вигнеровская кристаллизация [1], в которой кристаллическая решетка электронов образуется в результате их чисто отталкивающего кулоновского взаимодействия. Фактически, именно наблюдение особого поведения электронов на гелии явилось первой демонстрацией вигнеровской кристаллизации [2, 3]. Тем не менее, несмотря на ее кажущуюся простоту, еще многое предстоит узнать об этой сильно коррелированной системе и ее динамике вдали от теплового равновесия.Дэвид Рис и его коллеги из RIKEN, Япония, и Национального университета Цзяо Тунг, Тайвань, теперь наблюдали качественно новую и показательную особенность динамики кристалла Вигнера [4], движение электронной решетки при скольжении по гелию. поверхность в ответ на усиление электрического поля.

Поведение, наблюдаемое Рисом и его коллегами, очень отличается по природе от знакомого скачкообразного движения, встречающегося, например, при трении между двумя твердыми поверхностями.Здесь поведение прерывистого скольжения можно визуализировать, представив частицу, прикрепленную к пружине, которая тащит ее по потенциальному ландшафту с множеством минимумов, часто случайных по положению и высоте [5]. Если тяга пружины будет слишком слабой, частица застрянет в локальном минимуме, но как только сила тяги превысит критическое значение, частица будет перетянута через потенциальный барьер. Этот надбарьерный переход частично снимает напряжение в пружине и уменьшает силу, действующую на частицу, которая затем застревает в другом минимуме, пока напряжение снова не станет достаточно сильным.В этом суть атомистической картины трения Прандтля-Томлинсона, в которой поверхностные атомы создают потенциальный ландшафт. В чем-то похожая картина описывает динамику волн зарядовой или спиновой плотности, связанных со случайными центрами пиннинга в твердом теле [6].

Для электронов на гелии нет стационарного потенциала, чтобы закрепить кристалл Вигнера. Вместо этого движение кристалла ограничивается его взаимодействием с квантовым полем капиллярных волн на поверхности гелия; кванты поля этих волн называются рипплонами.Когда кристалл движется по поверхности гелия, электроны излучают рябь, подобно тому, как движущаяся лодка генерирует рябь на озере. Поскольку электроны передают импульс рипплонам, возникает сила реакции, отталкивающая электронный кристалл и замедляющая его. Теперь, если кристалл движется с низкой скоростью, испускаемые рипплоны не будут мешать друг другу. Но ситуация меняется, когда скорость кристалла приближается к фазовой скорости v0 рипплонов, распространяющихся в том же направлении и с длиной волны, равной межэлектронному расстоянию.Здесь, в простой картине, рипплоны, испускаемые разными электронами, движутся синфазно, и скорость испускания рипплонов резко возрастает. Это увеличение является результатом сочетания черенковского излучения рипплонов и их брэгговской дифракции, и оно дает силу реакции на электрон, которая зависит от числа электронов и расходится для бесконечного кристалла. Такое брэгговско-черенковское рассеяние [7] ограничивает теоретическую максимальную скорость кристалла Вигнера значением v0.

Насыщение скорости кристалла Вигнера при v0 было впервые получено из измерений, выполненных двадцать лет назад [8].Эксперимент Tour de Force, проведенный Рисом и его коллегами [4], показывает, что теперь возможно прямое измерение скорости кристалла. Исследователи использовали электрическое поле, чтобы прогнать электроны через канал длиной 100 мкм, заполненный гелием. Затем они измерили результирующий электронный ток (соответствующий скорости электронов) как функцию времени. Поле создавалось напряжением, которое прикладывалось между двумя металлическими пластинами, погруженными в гелий, и линейно нарастало во времени (рис. 1).Таким образом, сила, действующая на электроны, напоминала рывок все более растягивающейся пружины.

Исследователи обнаружили, что кристалл Вигнера быстро достигал v0, как только электрическое поле начало расти, двигаясь с этой скоростью в течение десятков микросекунд. Однако выше критического значения поля скорость кристалла подскочила выше v0 примерно на порядок. Результирующий перенос заряда привел к падению напряженности поля — сродни снятию напряжения в пружине — и возвращению скорости кристалла обратно к v0.В зависимости от температуры, команда наблюдала несколько всплесков скорости при одном увеличении напряжения, демонстрируя аналог поведения скачкообразного движения. Чтобы охарактеризовать это поведение, исследователи варьировали v0 (контролируя концентрацию электронов) и количество электронных рядов в канале. Это позволило им определить величину критического электрического поля и его зависимость от температуры и других параметров.

Наблюдаемые всплески тока представляют собой многочастичное неравновесное явление довольно общего, но пока неисследованного типа.Они соответствуют разрушению преграды, напоминающей преодоление звукового барьера высокоскоростным объектом. Ключевое отличие состоит в том, что барьер здесь является следствием сильных электронных корреляций и связи многоэлектронной системы с квантовым полем. Эта связь усиливается по мере приближения скорости кристалла к v0, что указывает как на сильную диссипацию, так и на сильное искажение поверхности гелия, что является многоэлектронным динамическим поляронным эффектом [9]. Используемая физика обширна и затрагивает многие аспекты физики конденсированных сред и статистической физики.Однако понять это — огромная проблема. Наблюдения Риса и его коллег дают важное понимание этой проблемы и делают ее доступной для экспериментов.

Это исследование опубликовано в журнале Physical Review Letters .

Список литературы

1. Вигнер Э. «О взаимодействии электронов в металлах», Phys. Ред. 46, , 1002 (1934).
2. С. Граймс и Г. Адамс, «Свидетельства о фазовом переходе жидкость-кристалл в классическом двумерном листе электронов», Phys.Rev. Lett. 42, , 795 (1979).
3. Д. С. Фишер, Б. И. Гальперин, П. М. Платцман, «Фонон-рипплоновая связь и двумерное электронное твердое тело на поверхности жидкий гелий», Phys. Rev. Lett. 42, , 798 (1979).
4. D. G. Rees, N. R. Beysengulov, J. -J. Линь, К. Коно, «Скачкообразное движение твердого тела Вигнера на жидком гелии», Phys. Rev. Lett. 116 , 206801 (2016).
5. А. Ваносси, Н. Манини, М. Урбах, С. Заппери и Э. Тосатти, «Коллоквиум: моделирование трения: от наномасштабов к мезомасштабам», Rev.Мод. Phys. 85 , 529 (2013).
6. П. Монсо, «Электронные кристаллы: экспериментальный обзор», Adv. Phys. 61 , 325 (2012).
7. Дикман М.И., Рубо Ю.Г. Брэгговско-черенковское рассеяние и нелинейная проводимость двумерного вигнеровского кристалла // ФММ. Rev. Lett. 78, , 4813 (1997).
8. А. Кристенсен, К. Джерфи, П. Фозоони, М. Дж. Ли, П. Дж. Ричардсон, А. Сантрих-Бадал, А. Блэкберн, Р. В. ван дер Хейден, «Магнитопроводимость с ограниченной холловской скоростью в классическом двумерном кристалле Вигнера. // Phys.Rev. Lett. 77, , 1350 (1996).
9. В. Ф. Винен, «Нелинейная электропроводность и скольжение в двумерном электронном кристалле на жидком гелии», J. Phys. Конденс. Дело 11, , 9709 (1999).

Об авторе

Марк Дайкман — профессор физики в Университете штата Мичиган. Он работал над различными темами, включая эффекты, возникающие в результате взаимодействия декогеренции, нелинейности и флуктуаций в мезоскопических колебательных системах; Динамика Флоке диссипативных систем; транспорт в коррелированных электронных системах; нелинейная оптика твердого тела; редкие события в системах, далеких от теплового равновесия; и многочастичные аспекты квантовой информации.Он является членом Американского физического общества. В 2013 году Американское физическое общество признало его выдающимся рефери.

---

Тематические области

Статьи по теме

Другие статьи

Вулканическая барабанная сейсмичность, вызванная скачкообразным движением и магматическим плавлением трением

1

Iverson, R.M. et al. Динамика сейсмогенной вулканической экструзии на горе Сент-Хеленс в 2004–05 гг. Nature 444 , 439–443 (2006).

Артикул Google Scholar

2

Коста, А., Уэдж, Г. и Мельник, О. Циклическое выдавливание лавового купола на основе механизма прерывистого скольжения. Планета Земля. Sci. Lett. 337–338 , 39–46 (2012).

Артикул Google Scholar

3

Neuberg, J. et al. Спусковой механизм низкочастотных землетрясений на Монтсеррате. J. Volcanol. Геотерм. Res. 153 , 37–50 (2006).

Артикул Google Scholar

4

Айверсон, Р.M. in Volcano Rekindled: New Eruption of Mount St Helens, 2004–2006 Professional Paper 1750 (ред. Шеррод, Д. Р., Скотт, В. Э. и Штауфер, П. Х.) Гл. 21, 425–460 (Геологическая служба США, 2008 г.).

Google Scholar

5

Шуэ, Б. А. и Матоза, Р. С. Многолетний обзор сейсмических методов обнаружения предвестников движения и извержения магмы. J. Volcanol. Геотерм. Res. 252 , 108–175 (2013).

Артикул Google Scholar

6

Michaut, C., Ricard, Y., Bercovici, D. & Sparks, R. S. J. Цикличность извержений кремнистых вулканов, потенциально вызванная волнами магматического газа. Nature Geosci. 6 , 856–860 (2013).

Артикул Google Scholar

7

Дмитриева К., Хотовец-Эллис А. Дж., Прежан С. и Данэм Э. М. Модель фрикционных разломов для гармонического тремора перед извержениями вулкана Редут. Nature Geosci. 6 , 652–656 (2013).

Артикул Google Scholar

8

Ленский, Н.Г., Спаркс, Р.С.Дж., Навон, О. и Ляховский, В. Циклическая активность на вулкане Суфриер-Хиллс, Монтсеррат: повышение давления, вызванное дегазацией, и экструзия прерывистого скольжения. Геол. Soc., Lond., Spec. Publ. 307 , 169–188 (2008).

Артикул Google Scholar

9

Tuffen, H., Смит, Р. и Саммондс, П. Р. Свидетельства сейсмогенного разрушения кремнистой магмы. Nature 453 , 511–514 (2008).

Артикул Google Scholar

10

Lavallée, Y. et al. Прогноз сейсмогенных лав и эксплозивных извержений. Природа 453 , 507–510 (2008).

Артикул Google Scholar

11

Lavallée, Y.и другие. Реконструкция разрушения магмы и проницаемой сети дегазации. Геология 41 , 515–518 (2013).

Артикул Google Scholar

12

Cashman, KV, Thornber, CR & Pallister, JS в Возрождение вулкана: новое извержение горы Сент-Хеленс, 2004-2006 гг. Professional Paper 1750 (ред. Sherrod, DR, Scott, WE & Stauffer, PH ) Гл. 19, 387–413 (Геологическая служба США, 2008).

Google Scholar

13

Кеннеди, Л. А., Рассел, Дж. К. и Неллес, Э. Происхождение катаклазитов горы Сент-Хеленс: экспериментальные выводы. Am. Минеральная. 94 , 995–1004 (2009).

Артикул Google Scholar

14

Мур, П. Л., Айверсон, Н. Р. и Айверсон, Р. М. в книге Возрождение вулкана: новое извержение горы Сент-Хеленс, 2004-2006 гг.Р., Скотт, В. Э. и Штауфер, П. Х.) гл. 20, 415–424 (Геологическая служба США, 2008 г.).

Google Scholar

15

Kendrick, J. E. et al. Экстремальные фрикционные процессы в канале вулкана на горе Сент-Хеленс (США) во время извержения 2004–2008 гг. J. Struct. Геол. 38 , 61–76 (2012).

Артикул Google Scholar

16

Дитрих, Дж. Х.Моделирование трения горных пород: I Результаты экспериментов и определяющие уравнения. J. Geophys. Res. Твердая Земля 84 , 2161–2168 (1979).

Артикул Google Scholar

17

Хиросе, Т. и Шимамото, Т. Расстояние ослабления скольжения разломов во время плавления трением, выведенное из экспериментальных и естественных псевдотахилитов. Bull. Сейсмол. Soc. Являюсь. 95 , 1666–1673 (2005).

Артикул Google Scholar

18

Нимейер, А.Р., Ди Торо, Г., Нильсен, С. и Ди Феличе, Ф. Фрикционное плавление габбро в экстремальных экспериментальных условиях нормального напряжения, ускорения и скорости скольжения. J. Geophys. Res. Твердая Земля 116 , B07404 (2011).

Артикул Google Scholar

19

Lavallée, Y. et al. Экспериментальная генерация вулканических псевдотахилитов: сдерживающая реология. J. Struct. Геол. 38 , 222–233 (2012).

Артикул Google Scholar

20

Фиалко Ю. и Хазан Ю. Синтез при трении при землетрясении: прилипание или скольжение? J. Geophys. Res. Твердая Земля 110 , B12407 (2005).

Артикул Google Scholar

21

Спрей, Дж. Г. Процессы фрикционного плавления в планетных материалах: от удара на сверхвысокой скорости до землетрясений. Ann. Преподобный «Планета Земля».Sci. 38 , 221–254 (2010).

Артикул Google Scholar

22

Ди Торо, Г., Хиросе, Т., Нильсен, С., Пеннаккиони, Г. и Шимамото, Т. Естественные и экспериментальные доказательства смазывания разломов расплавом во время землетрясений. Наука 311 , 647–649 (2006).

Артикул Google Scholar

23

Hale, A. J. & Wadge, G.Переход от эндогенного к экзогенному росту лавовых куполов с развитием полос сдвига. J. Volcanol. Геотерм. Res. 171 , 237–257 (2008).

Артикул Google Scholar

24

Ди Торо, Г. и др. Неисправная смазка при землетрясениях. Nature 471 , 494–498 (2011).

Артикул Google Scholar

25

Нода, Х., Канагава, К., Хиросе, Т. и Иноуэ, А. Эксперименты по трению долерита при промежуточных скоростях скольжения с контролируемой температурой: ослабление скорости или ослабление температуры? J. Geophys. Res. Твердая Земля 116 , B07306 (2011).

Артикул Google Scholar

26

Байерли, Дж. Д. Трение горных пород. Pure Appl. Geophys. 116 , 615–626 (1978).

Артикул Google Scholar

27

Нильсен, С., Ди Торо, Г., Хиросе, Т. и Шимамото, Т. Фрикционный расплав и сейсмическое скольжение. J. Geophys. Res. Твердая Земля 113 , B01308 (2008).

Артикул Google Scholar

28

Лавалле Ю., Гесс К. У., Кордонье Б. и Дингвелл Д. Б. Неньютоновский реологический закон для высококристаллических купольных лав. Геология 35 , 843–846 (2007).

Артикул Google Scholar

29

Джордано, Д., Рассел, Дж. К. и Дингвелл, Д. Б. Вязкость магматических жидкостей: модель. Планета Земля. Sci. Lett. 271 , 123–134 (2008).

Артикул Google Scholar

30

Хаммер, К. и Нойберг, Дж. У. О динамическом поведении роев низкочастотных землетрясений перед обрушением купола вулкана Суфриер-Хилл, Монтсеррат. Geophys. Res. Lett. 36 , L06305 (2009).

Артикул Google Scholar

31

Шимамото, Т.И Цуцуми А. Новая высокоскоростная машина для испытания на трение с роторным сдвигом: основная конструкция и объем исследований. Struct. Геол. 39 , 65–78 (1994).

Google Scholar

Летние суточные и зимние многодневные скачкообразные движения, вызванные поверхностным таянием, и седиментология

1.

Фонтан, А. Г. и Уолдер, Дж. С. Поток воды через ледники умеренного пояса. Rev. Geophys. 36 , 299–328 (1998).

ADS Статья Google Scholar

2.

Бултон, Г. С., Добби, К. Э. и Зацепин, С. Деформация отложений под ледниками и ее связь с подледниковой гидравлической системой. Quat. Int. 86 , 3–28 (2001).

Артикул Google Scholar

3.

Damsgaard, A. et al. Динамика ледяного потока, обусловленная колебаниями давления воды в подледниковых зернистых пластах. Geophys. Res. Lett. 43 , https://doi.org/10.1002/2016GL071579 (2016).

4.

Икен А. и Биндшадлер Р. А. Комбинированные измерения давления подледниковой воды и скорости поверхности Финделенглетчера, Швейцария: выводы о дренажной системе и механизме скольжения. J. Glaciol. 32 , 101–119 (1986).

ADS Статья Google Scholar

5.

Андерсон Р.S. et al. Сильная обратная связь между гидрологией и скольжением небольшого альпийского ледника. J. Geophys. Res .: Earth Surf. 109 , 2156–2202 (2004).

Google Scholar

6.

Сугияма, С. и Гудмундссон, Х. Г. Краткосрочные колебания ледникового потока, контролируемые давлением подледниковой воды в Лаутераарглетшере, Бернские Альпы, Швейцария. J. Glaciol. 50 , 353–362 (2004).

ADS CAS Статья Google Scholar

7.

Стивенс, Л. А. и др. Реакция стока Гренландского ледникового щита на изменчивость стока. Geophys. Res. Lett ., 43 , https://doi.org/10.1002/2016GL070414 (2016).

8.

Кларк, Г. К., Коллинз, С. Г. и Томпсон, Д. Э. Течение, термическая структура и подледниковые условия ледника нагонного типа. Can. J. Земля. Sci. 21 , 232–240 (1984).

ADS Статья Google Scholar

9.

Камб, Б. Механизм нагона ледников, основанный на конфигурации связанных полостей в системе основных водоводов. J. Geophys. Источник: Solid Earth 92 (B9), 9083–9100 (1987).

Артикул Google Scholar

10.

Роуз К.Э. Характеристики ледового потока на Земле Мэри Берд в Антарктиде. J. Glaciol. 24 , 63–75 (1979).

ADS Статья Google Scholar

11.

Шольц, К. Х. Землетрясения и законы трения. Nature 391 , 37 (1998).

ADS CAS Статья Google Scholar

12.

Фишер, У. Х. и Кларк, Дж. К. К. Поведение при скачкообразном скольжении у подножия ледника. Ann. Glaciol. 24 , 390–396 (1997).

ADS Статья Google Scholar

13.

Смит, А.М. Микроземлетрясения и подледниковые условия. Geophys. Res. Lett. 33 , L24501 (2006).

ADS Статья Google Scholar

14.

Винс, Д. А., Анандакришнан, С., Винберри, Дж. П. и Кинг, М. А. Одновременные телесейсмические и геодезические наблюдения за скачкообразным движением антарктического ледяного потока. Nature 453 , 770–774 (2008).

ADS CAS Статья Google Scholar

15.

Гольдберг, Д. Н., Шуф, С., Сергиенко, О. В. Скачкообразное движение антарктического ледяного потока: эффекты вязкоупругости. J. Geophys. Res .: Earth Surf. 119 , 1564–1580 (2014).

ADS Статья Google Scholar

16.

Винберри, Дж. П., Анандакришнан, С., Элли, Р. Б., Биндшадлер, Р. А. и Кинг, М. А. Базовая механика ледяных потоков: выводы из скачкообразного движения ледяного потока Уилланс, Западная Антарктида. J. Geophys. Res .: Earth Surf. 114 , F01016 (2009).

ADS Статья Google Scholar

17.

Липовский Б. П. и Данхэм Э. М. Тремор во время скачкообразного движения ледяного потока. Криосфера 10 , 385–399 (2016).

ADS Статья Google Scholar

18.

Липовский Б. П. и Данэм Э. М. Медленное скольжение на ледяной равнине Уилланс в Антарктиде, описанное с использованием трения скорости и состояния в качестве закона скольжения ледяного потока. J. Geophys. Res. 122 , 973–1003 (2017).

Артикул Google Scholar

19.

Zoet, L. K. et al. Влияние увлеченного мусора на базальную устойчивость ледника к скольжению. J. Geophys. Res .: Earth Surf. 118 , 656–666 (2013).

ADS Статья Google Scholar

20.

Райс, Дж. Р., Надия, Л. и Ранджит, К.Трение, зависящее от скорости и состояния, и стабильность скольжения между упруго деформируемыми твердыми телами. J. Mech. Phys. Твердые тела 49 , 1865–1898 (2001).

ADS Статья Google Scholar

21.

Ратбун, А. П., Мароне, К., Элли, Р. Б., Анандакришнан, С. Лабораторные исследования реологии трения сдвигового тила. J. Geophys. Res .: Earth Surf. 113 , F02020 (2008).

ADS Статья Google Scholar

22.

Мур, П. Л. и Айверсон, Н. Р. Медленный эпизодический сдвиг гранулированных материалов, регулируемый дилатантным упрочнением. Геология 30 , 843–846 (2002).

ADS Статья Google Scholar

23.

Ратбун А. П. и Мароне К. Влияние локализации деформации на фрикционное поведение измельченных гранулированных материалов. J. Geophys. Источник: Solid Earth 115 , B01204 (2010).

ADS Статья Google Scholar

24.

Маккарти, К., Сэвидж, Х. и Неттлс, М. Температурная зависимость трения льда о камень в реальных ледниковых условиях. Philos. Пер. R. Soc. А 375 , 2086 (2017).

Артикул Google Scholar

25.

Биндшадлер, Р. А., Кинг, М. А., Элли, Р. Б., Анандакришнан, С. и Падман, Л. Контролируемый приливом сток из ледяного потока Западной Антарктики. Наука 301 , 1087–1089 (2003).

ADS CAS Статья Google Scholar

26.

Вальтер, Ф., Дайхманн, Н. и Функ, М. Базальные ледотрясения во время изменения давления подледниковой воды под Горнерглетшером, Швейцария. J. Glaciol. 54 , 511–521 (2008).

ADS Статья Google Scholar

27.

Рётлисбергер, Х. Давление воды во внутри- и подледниковых каналах. J. Glaciol. 11 , 177–203 (1972).

ADS Статья Google Scholar

28.

Хок, Р. и Хук, Р. Л. Эволюция внутренней дренажной системы в нижней части зоны абляции Storglaciären. Swed. Геол. Soc. Являюсь. Бык. 105 , 537–546 (1993).

ADS Статья Google Scholar

29.

Крейтс, Т.T. & Schoof, C.G. Дренаж через подледниковые водные покровы. J. Geophys. Res .: Earth Surf. 114 , F04008 (2009).

ADS Статья Google Scholar

30.

Шредер Д. М., Бланкеншип Д. Д. и Янг Д. А. Свидетельства перехода водной системы под ледником Туэйтс в Западной Антарктиде. Proc. Natl Acad. Sci. США 110 , 12225–12228 (2013).

ADS CAS Статья Google Scholar

31.

Пиментель, С. и Флауэрс, Г. Э. Численное исследование гидрологической динамики ледников и подледниковых затоплений. Proc. R. Soc. Лондон. А 467 , 537–558 (2011).

ADS MathSciNet Статья Google Scholar

32.

Бултон Г. С. и Хиндмарш Р. К. Деформация отложений под ледниками: реология и геологические последствия. J. Geophys. Источник: Solid Earth 92 (B9), 9059–9082 (1987).

Артикул Google Scholar

33.

Камб Б. Реологическая нелинейность и неустойчивость течения в деформирующем механизме движения ледяной струи. J. Geophys. Источник: Solid Earth 96 (B10), 16585–16595 (1991).

Артикул Google Scholar

34.

Хиндмарш Р. Деформирующие пласты: вязкие и пластические масштабы деформации. Quat.Sci. Ред. , , 16, , 1039–1056 (1997).

ADS Статья Google Scholar

35.

Айверсон, Н. Р., Хойер, Т. С. и Бейкер, Р. В. Исследования деформации тилла с помощью кольцевого сдвига: кулон-пластическое поведение и распределенная деформация в ложах ледников. J. Glaciol. 44 , 634–642 (1998).

ADS Статья Google Scholar

36.

Altuhafi, F.Н., Боде Б. А. и Саммондс П. О зависимости от времени поведения ледниковых отложений: геотехнический подход. Quat. Sci. Ред. 28 , 693–707 (2009).

ADS Статья Google Scholar

37.

Харт, Дж. К., Роуз, К. К. и Мартинез, К. Поведение подледникового тилла, полученное на основе беспроводных мультисенсорных подледниковых зондов: реология, гидромеханические взаимодействия и формирование тилла. Quat.Sci. Ред. 30 , 234–247 (2011).

ADS Статья Google Scholar

38.

Харт, Дж. К. и Бултон, Г. С. Взаимосвязь гляциотектонических и ледниковых процессов в ледниковой среде. Quat. Sci. Rev. 10 , 335–350 (1991).

ADS Статья Google Scholar

39.

Кларк, Г. К.C. Подледниковые процессы. Annu. Преподобный Земля. Планета. Sci. 33 , 247–276 (2005).

ADS MathSciNet CAS Статья Google Scholar

40.

Айверсон, Н. Р. Сопротивление сдвигу и непрерывность подледникового тилла: правила гидрологии. J. Glaciol. 56 , 1104–1114 (2010).

ADS Статья Google Scholar

41.

Фишер У. Х. и Кларк Г. К. Обзор подледниковой гидромеханической связи: ледник Трапридж, территория Юкон, Канада. Quat. Int. 86 , 29–43 (2001).

Артикул Google Scholar

42.

Мюррей Т. и Портер П. Р. Базальные условия под мягким слоем политермального ледника нагонного типа: Баканинбреен, Шпицберген. Quat. Int. 86 , 103–116 (2001).

Артикул Google Scholar

43.

Аллея, Р. Б. В поисках липких мест на ледяном потоке. J. Glaciol. 39 , 447–454 (1993).

ADS Статья Google Scholar

44.

Hart, J. K., Rose, K. C., Clayton, A. & Martinez, K. Englacial и подледниковый поток воды в Скалафелльсьёкюдле, Исландия, полученный с помощью георадара, зонда Glacsweb и измерений уровня воды в скважинах. Earth Surf. Процесс. Landf. 40 , 2071–2083 (2015).

ADS Статья Google Scholar

45.

Харт, Дж. К. и Мартинес, К. Сети датчиков окружающей среды: революция в науке о земных системах? Earth-Sci. Ред. 78 , 177–191 (2006).

ADS Статья Google Scholar

46.

Martinez, K. et al. Сеть беспроводных датчиков геофона для исследования скачкообразного движения ледника. Comput. Geosci. 105 , 103–112 (2017).

ADS Статья Google Scholar

47.

Nienow, P. W. et al. Гидрологический контроль суточной изменчивости ледяного потока в долинных ледниках. J. Geophys. Res .: Earth Surf. 110 (F4), 2156–2202 (2005).

Артикул Google Scholar

48.

Гош, С. К. и Рамберг, Х.Переориентация включений путем сочетания чистого сдвига и простого сдвига. Тектонофизика 34 , 1–70 (1976).

ADS Статья Google Scholar

49.

Айверсон, Н. Р., Хэнсон, Б., Гук, Р. Л., Янссон, П. Механизм течения ледников на мягких пластах. Science 267 , 80–81 (1995).

ADS CAS Статья Google Scholar

50.

Бултон, Г. С. и Добби, К. Э. Уплотнение отложений ледниками: взаимосвязь между геотехникой отложений, динамикой мягких ледников и подледниковым потоком грунтовых вод. J. Glaciol. 39 , 26–44 (1993).

ADS Статья Google Scholar

51.

Бартоломаус, Т. К., Андерсон, Р. С. и Андерсон, С. П. Реакция базального движения ледника на временное накопление воды. Nat. Geosci. 1 , 33–37 (2008).

ADS CAS Статья Google Scholar

52.

Sole, A. et al. Зимнее движение опосредует динамическую реакцию ледникового щита Гренландии на более теплое лето. Geophys. Res. Lett. 40 , 3940–3944 (2013).

ADS Статья Google Scholar

53.

Эванс, Д. Дж. А., Филлипс, Э. Р., Хиемстра, Дж. Ф. и Аутон, К. А. Подледниковый тилль: формирование, характеристики осадочных пород и классификация. Earth-Sci. Ред. 78 , 115–176 (2006).

ADS Статья Google Scholar

54.

Мензис Дж. Пути деформации до внутренней архитектуры и микроструктуры — перспективы общей кинематической модели — «план» для развития тилла. Quat. Sci. Ред. 50 , 105–124 (2012).

ADS Статья Google Scholar

55.

Харт, Дж. К. Подледниковый тиллообразование: микромасштабные процессы в зоне подледникового сдвига. Quat. Sci. Ред. 170 , 26–44 (2017).

ADS Статья Google Scholar

56.

Харт, Дж. К., Роуз, К. К., Мартинез, К. и Онг, Р. Поведение подледниковых обломков и его значение для развития ткани тилла: новые результаты, полученные в экспериментах с беспроводными подледными зондами. Quat. Sci. Ред. 28 , 597–607 (2009).

ADS Статья Google Scholar

57.

Hooyer, T. S. & Iverson, N. R. Развитие обломочной ткани в расслаивающемся зернистом материале: последствия для подледникового тилла и борозды по разломам. Геол. Soc. Являюсь. Бык. 112 , 683–692 (2000).

ADS Статья Google Scholar

58.

Zwally, H.J. et al. Ускорение течения гренландского ледникового покрова, вызванное поверхностным таянием. Наука 297 , 218–222 (2002).

ADS CAS Статья Google Scholar

59.

Sundal, A. V. et al. Ускорение ледникового покрова Гренландии, вызванное таянием, компенсируется эффективным подледным дренажем. Природа 469 , 521–524 (2011).

ADS CAS Статья Google Scholar

60.

Tedstone, A.J. et al. Десятилетнее замедление движения к суше в секторе Гренландского ледникового щита, несмотря на потепление. Природа 526 , 692–695 (2015).

ADS CAS Статья Google Scholar

61.

Minchew, B. et al. Пластиковый слой под ледяной шапкой Хофсйёкюдль в центральной Исландии и чувствительность ледяного потока к поверхностному потоку талой воды. J. Glaciol. 62 , 147–158 (2016).

ADS Статья Google Scholar

62.

Мартинес, К., Харт, Дж. К. и Онг, Р. в GeoSensor Networks (ред. Тригони, Н., Маркхам А. и Наваз, С.) 5659 (Springer, Berlin, Heidelberg, 2009).

63.

Мюррей Т. и Кларк Г. К. Моделирование подледниковой водной системы методом черного ящика. J. Geophys. Источник: Solid Earth 100 (B6), 10231–10245 (1995).

Артикул Google Scholar

64.

Hooke, R. Le. Б., Калла, П., Холмлунд, П., Nilsson, M. & Stroeven, A. Трехлетняя запись сезонных колебаний поверхностной скорости, Сторгласиарен, Швеция. J. Glaciol. 35 , 235–247 (1989).

ADS Статья Google Scholar

65.

Трюфер М., Эчелмейер К. А. и Харрисон В. Д. Влияние деформации тилла на динамику ледников. J. Glaciol. 47 , 123–134 (2001).

ADS Статья Google Scholar

66.

Хок Р. Моделирование температурного индекса в горных районах. J. Hydrol. 282 , 104–115 (2003).

ADS Статья Google Scholar

67.

Йоханнессон, Т., Сигурдссон, О., Лауманн, Т. и Кеннетт, М. Моделирование баланса массы ледников в градусах суток с приложениями к ледникам Исландии, Норвегии и Гренландии. J. Glaciol. 41 , 345–358 (1995).

ADS Статья Google Scholar

68.

Причард, Х., Мюррей, Т., Лакман, А., Строцци, Т. и Барр, С. Динамика нагонов ледников в Сортебро, восточная Гренландия, по данным слежения за объектами радара с синтезированной апертурой. J. Geophys. Res. 110 , F03005 (2005).

ADS Статья Google Scholar

69.