Проверить геометрию кузова: Как проверить геометрию кузова, проверка правильности геометрии кузова авто

Содержание

что такое, как проверить, признаки нарушения геометрии

Проверка геометрии кузова поможет узнать, был ли автомобиль в серьезных авариях. Не помешает она и машине, прошедшей более 100 тысяч километров без ДТП. Рассказываем, как проверить состояние кузова самостоятельно и в сервисном центре.

Что называют геометрией кузова?

Под геометрией автомобиля понимают расположение силовых элементов кузова друг относительно друга. В норме все расстояния соответствуют параметрам, рассчитанным производителем при разработке модели. При появлении отклонений начинаются проблемы.

Чаще всего геометрию кузова проверяют при покупке подержанного автомобиля. Это лучший способ узнать, была ли машина в ДТП. Если осмотр и тесты показывают легкие деформации, вы можете требовать скидку у продавца. При серьезных повреждениях от покупки лучше отказаться.

Мастера-кузовщики также рекомендуют проверять геометрию кузова каждые 100 тысяч километров, даже если машина не была в авариях.

Езда по неровным дорогам, сильный износ подвески, наезды на препятствия и даже долгие стоянки с перекосом (например, одной стороной на бордюре) могут деформировать каркас авто. Чем раньше вы займетесь ремонтом, тем меньше проблем будет в будущем.

Какие отклонения обычно выявляет проверка?

Длина лонжеронов не совпадает — был серьезный удар с одной стороны.
Смят моторный щит или поперечина позади салона — автомобиль был в тяжелом ДТП, затронувшем почти весь кузов.
Погнуты стойки крыши — вероятнее всего, машина переворачивалась.
Дверцы провисают или неплотно закрываются — был боковой удар или у автомобиля очень большой пробег.
Плохо закрывается капот или багажник — был сильный удар спереди либо сзади.
Расстояния между колесами отличаются — машину не щадили, кузов деформирован из-за быстрой езды по плохим дорогам.
Опоры двигателя неровные, мотор перекошен — автомобиль подпрыгивал на неровностях и очень жестко приземлялся.

Как проверить геометрию кузова самостоятельно?

Визуальный осмотр

Начните со стекол. Верный признак нарушения геометрии кузова — горизонтальные трещины. Деформированный кузов сильно сдавливает стекло, поэтому со временем оно начинает лопаться.

Откройте водительскую дверь, покачайте вверх-вниз, закройте. Если она сильно шатается и стучит, петли установлены неровно или ослаблены. Если дверца закрывается с большим усилием, проем наверняка перекошен.

Посмотрите на зазоры между кузовными панелями, приложите к ним палец для оценки размеров. Неровные щели означают, что машина побывала в серьезной аварии. Еще один повод насторожиться — неоднородная окраска. Разница в цвете говорит о том, что автомобиль красили. В большинстве случаев кузовной ремонт делают после ДТП.

Проверка рулеткой

Структура кузова автомобиля может быть сложной, поэтому геометрию лучше всего проверять по колесам. Вначале измерьте колесную базу справа и слева — расстояние между передней и задней ступицей.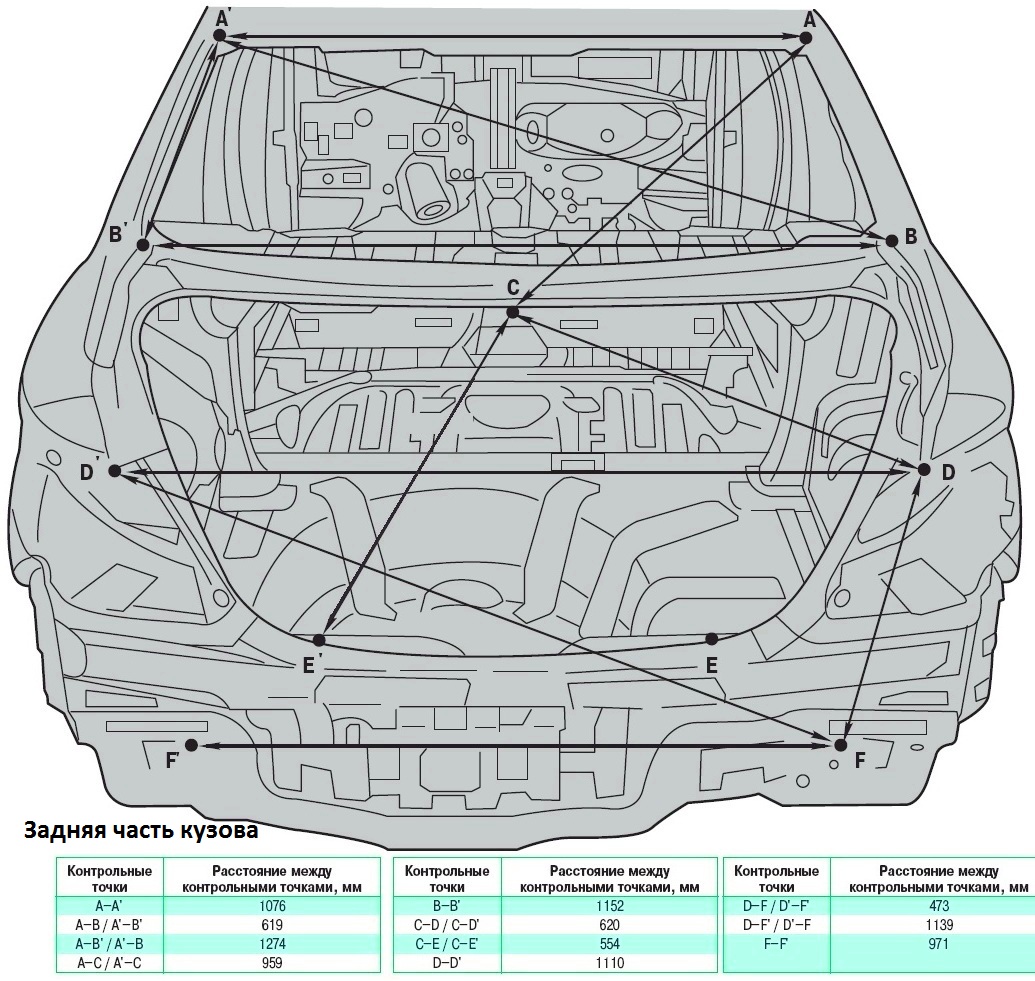

Цифры должны быть одинаковы. Затем уточните колею спереди и сзади — дистанцию от середины протектора правого колеса до середины протектора левого. Здесь допускаются различия, поэтому результаты лучше сверять с техническими характеристиками автомобиля. Их можно найти в инструкции по эксплуатации или в интернете.

Можно проверить геометрию кузова своими руками, замерив ширину дверного проема автомобиля у нижней и верхней петли. Посмотрите на длину проема багажника от крышки до кромки в 2–3 точках, а также длину подкапотного пространства. Разница в пару миллиметров допустима — мы уже говорили о последствиях езды по некачественным дорогам. А вот более серьезные отклонения будут поводом насторожиться.

h3 Профессиональная проверка геометрии кузова в автосервисе

Проверка инструментами

Специалисты измеряют расстояние между контрольными точками электронным штангенциркулем с погрешностью не более 0,1 мм. Они оценивают взаимное положение кузовных панелей и силовых элементов с разных сторон, сравнивая результаты между собой.

Для измерения колесной базы, колеи и длины лонжеронов используется масштабная рейка. Мастер устанавливает ее рядом с автомобилем и выбирает нужные точки замера — на экране появляется точное расстояние.

Автоматизированная проверка

Крупные СТО и официальные сервисные центры используют компьютерные стенды. Автомобиль загоняют на подъемник, а затем приклеивают метки к контрольным точкам. Камеры измеряют основные показатели геометрии кузова за считанные секунды.

В официальных сервисных центрах Mercedes-Benz, Porsche, Cadillac и других престижных брендов могут использоваться лазерные стенды. Они проверяют геометрию кузова автомобиля без меток, сравнивая ее с параметрами завода-изготовителя. Автоматика исключает человеческий фактор — погрешность измерения не превышает 0,5 %.

Чем плоха нарушенная геометрия кузова?

Хуже всего, что поврежденный автомобиль непредсказуемо ведет себя в последующих ДТП. Нередки случаи, когда при легких столкновениях блокируются двери, смещается руль и перекашивает двигатель. Системы пассивной безопасности, заложенные производителем на стадии проектирования, перестают работать и наносят дополнительный вред пассажирам.

Есть и другие неприятные последствия нарушенной геометрии:

ускоренный износ подвески, полуосей и шин;
посторонние звуки на малой скорости;
попадание пыли, воды и грязи в салон;
неплотно закрывающиеся двери, которые легко взломать;
ошибки электроники;
сильные вибрации и тряска на малейших неровностях;
увод автомобиля в сторону на скорости 50–100 км/ч.

Как исправить геометрию автомобиля?

Ремонтом занимаются специализированные кузовные СТО. Машину разбирают, чтобы добраться до силовой структуры. Мастер проводит замеры по контрольным точкам, чтобы определить степень деформации с точностью до миллиметра.

Геометрию кузова автомобиля восстанавливают на стапелях. Их крюки цепляются за технологические отверстия в каркасе машины. Специалист выбирает расстояние, на которое нужно сместить силовые элементы. Высокоточная гидравлика выполняет его команды, подтягивая крюки цепями.

Нужно помнить, что у металла есть предел прочности. Сильные удары нарушают его структуру на молекулярном уровне, вызывая «усталость». Если кузов серьезно поврежден, проблемы будут появляться даже после восстановления геометрии. Поэтому при покупке подержанной машины нужно знать, в каких авариях она побывала.

Проверка геометрии кузова в г.Уфа

Проверка геометрии в сервисе

За время своей эксплуатации автомобиль с различной степенью вероятности может попасть в ДТП, получить повреждения. Если это произошло, то ему предстоит ремонт, восстановление ЛКП и как водится проверка восстановленной геометрии, с использованием значений контрольных точек замера кузова.

Размеры и их значение

Точные размеры легкового или грузового авто, задаваемые заводом-изготовителем — это геометрия деталей кузова.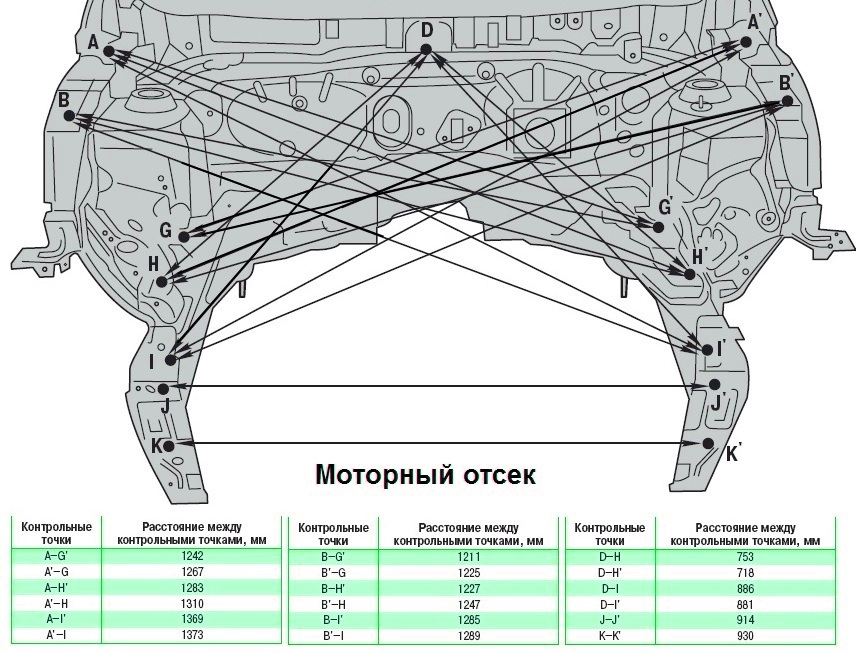 Размеры делятся на две большие группы: основные, наиболее важные в плане информативности и дополнительные, информация о которых необходима, но менее важна. Стандартная послеремонтная проверка оптимальной (правильной) полученной геометрии современного кузова, наиболее значимые размеры:

Замеряемая ширина, в миллиметрах, передней колеи;

Замеряемая ширина, в миллиметрах, задней колеи;

Общая длина измеренной колесной базы;

Имеющаяся реальная длина всех конструктивных автомобильных лонжеронов на момент проверки, расстояние, измеренное в миллиметрах, между этими узлами.

Как проводится рутинная инструментальная проверка восстановленной в результате проведенных работ геометрии отремонтированного в автомобильном сервисе кузова, что является главным при проведении измерений? Измеряемая колея – это расстояние между двумя колесами автомобиля, расположенными попарно на одной воображаемой оси. Передняя колея – фактически это полученное в результате расстояние в мм, замеренное мастером между обоими передними колесами, задняя колея, соответственно расстояние, имеющееся между задними автомобильными колесами.

Колесная база – полученное расстояние от передней оси автомобиля до задней. Проверка контрольных параметров геометрии любого кузова подразумевает оценку расстояния от точки центра ступиц передней оси до центра ступиц задней оси – это так называемая измеряемая длина колесной базы. Лонжероны современного автомобиля – это компоненты силового каркаса, его основа. Именно к лонжеронам крепятся перегородки, все крылья, пол транспортного средства, ДВС или дизель, коробка передач, оба бампера, рулевая колонка и все несущие элементы конструкции авто.

Проверка элементов

Когда же в автосервисе проводится текущая проверка имеющейся правильной геометрии интересующего нас кузова? Обычно она происходит при покупке поддержанного авто и является одним из аргументов для принятия решения, и после проведения любого кузовного ремонта, здесь она проводится для того, чтобы достоверно оценить, с каким качеством был проведен ремонт. Когда автомобиль новый, пахнет заводской краской, только что сошел с конвейера, здесь беспокоиться не о чем. Дополнительная же проверка совершенной геометрии автомобильного кузова в этом случае не нужна, так все детали новенького авто симметричны и геометрия кузова идеальна. Но, наконец, начинается эксплуатация транспортного средства и, несмотря на то обстоятельство, что все неподвижные детали авто жестко закреплены, правильная геометрия понемногу нарушается, а если транспортное средство попало в ДТП, то после проведения ремонта обязательно проводится контрольная (окончательная) проверка восстановленной персоналом сервиса геометрии отремонтированного и покрашенного кузова.

Особенности проведения работ

В технической документации на автомобиль всегда есть важный раздел, в котором указывается расстояние между различными контрольными точками. Концерн-производитель авто при этом предполагает, что все контрольные точки находятся в допуске, если это действительно так, все двери без приложения усилия закрываются, поверхность капота, крышки авто багажника и дверей плотно, без зазоров прилегают к кузову.

Если же это не так, проводится скрупулезная проверка всей необходимой геометрии измеряемой у кузова автомобиля. Только после этого можно проводить процедуру регулировки развала-схождения. На современных станциях технического обслуживания, таких как, к примеру, автосервис «Автоформен» проверка полученной геометрии клиентского кузова проводится с помощью специального стенда, где вся информация выводится на экран персонального компьютера.

Проведение поверки в сервисе «Автоформен»

Выполнить все кузовные мероприятия и восстановить утраченную геометрию кузова вы можете в нашем специализированном кузовном центре. Он находится в городе Уфе, по адресу: ул. Трамвайная, 2 В. Специалистами нашего предприятия здесь же, на месте, будет проведена необходимая проверка восстановленной после проведения ремонта геометрии поврежденного в ДТП кузова автомобиля. Записаться для проведения осмотра, ремонта и обслуживания вы можете по контактному телефону +7 (347) 216-67-97.

Почему так важно проверять геометрию кузова своего авто? Как это сделать?

Правильная геометрия кузова — одно из важнейших условий для долгой и беспроблемной эксплуатации автомобиля. К сожалению, многие автовладельцы никогда не проверяют корпус машины на отсутствие деформаций. Они считают, что если авто не было в ДТП, то геометрия кузова должна оставаться идеальной.

На самом деле, деформации могут вызываться не только сильными ударами. В процессе езды по участкам дороги со сложным рельефом, при попадании в глубокие ямы, при спуске с крутых уклонов несущие элементы кузова также могут искривляться.

Нарушение геометрии может быть визуально заметным и проявляться в виде увеличившихся зазоров между элементами корпуса, в незакрывающихся дверях, капоте или багажнике. Те деформации, которые не обнаруживаются при внешнем осмотре машины, вызывают увеличение нагрузки на ходовую часть и ускоряют износ комплектующих, снижают управляемость транспортного средства. Поэтому очень важно периодически проводить проверку корпуса машины и устранять обнаруженные дефекты.

Как проверяется геометрия кузова авто?

Автомобильный каркас рассматривается как совокупность контрольных точек, которые должны располагаться на определенном расстоянии друг от друга. Эти расстояния указываются производителями транспортных средств. Наиболее важными для комфортной и безопасной эксплуатации машины является сохранение нормативных расстояний между несущими элементами корпуса: стойками, стаканам, лонжеронами и другими.

Проверку геометрии кузова можно выполнить самостоятельно, если найти соответствующие данные производителя машины. Но точность замеров в домашних условиях не будет достаточной. Чтобы быть полностью уверенными в отсутствии деформаций корпуса, воспользуйтесь услугами нашего автосервиса. Мы проводим проверку геометрии кузова на специализированном оборудовании с электронными измерительными приборами и гарантируем высокую точность замеров.

Как делается проверка геометрии кузова автомобиля

Если вы приняли решение приобрести новенькое авто в автосалоне, вас вряд ли будет одолевать вопрос, что такое геометрия кузова и как её проверить. Ни один уважающий себя автопроизводитель не допустит выпуска транспортных средств с явными дефектами, поскольку это приведёт к потере потенциальных клиентов, резкому снижению уровня их доверия. Потерять доверие клиентов можно молниеносно, а вот восстановить его, вернуть себе собственное имя — сложно, для этого потребуется большое количество времени. Иное дело, когда вы решаетесь на приобретение транспортного средства с уже имеющимся автопробегом. Вы не владеете информацией относительно его прошлого, вы ничего не знаете о том, в каких условиях оно эксплуатировалось. Опираться на информацию владельца, конечно же, нельзя, поскольку он является заинтересованным лицом, стремящимся продать свой автомобиль по более выгодной стоимости. Вот именно в таких случаях необходимо тщательно осмотреть транспортное средство, а также измерить расстояние между контрольными точками, проверив геометрию кузова.

Что такое геометрия кузова

Большинство автовладельцев безошибочно ответят, что любое транспортное средство представляет собой симметричный объект. При неправильной эксплуатации, попадании транспортного средства в ДТП симметричность нарушается. Игнорировать такие нарушения ни в коем случае нельзя.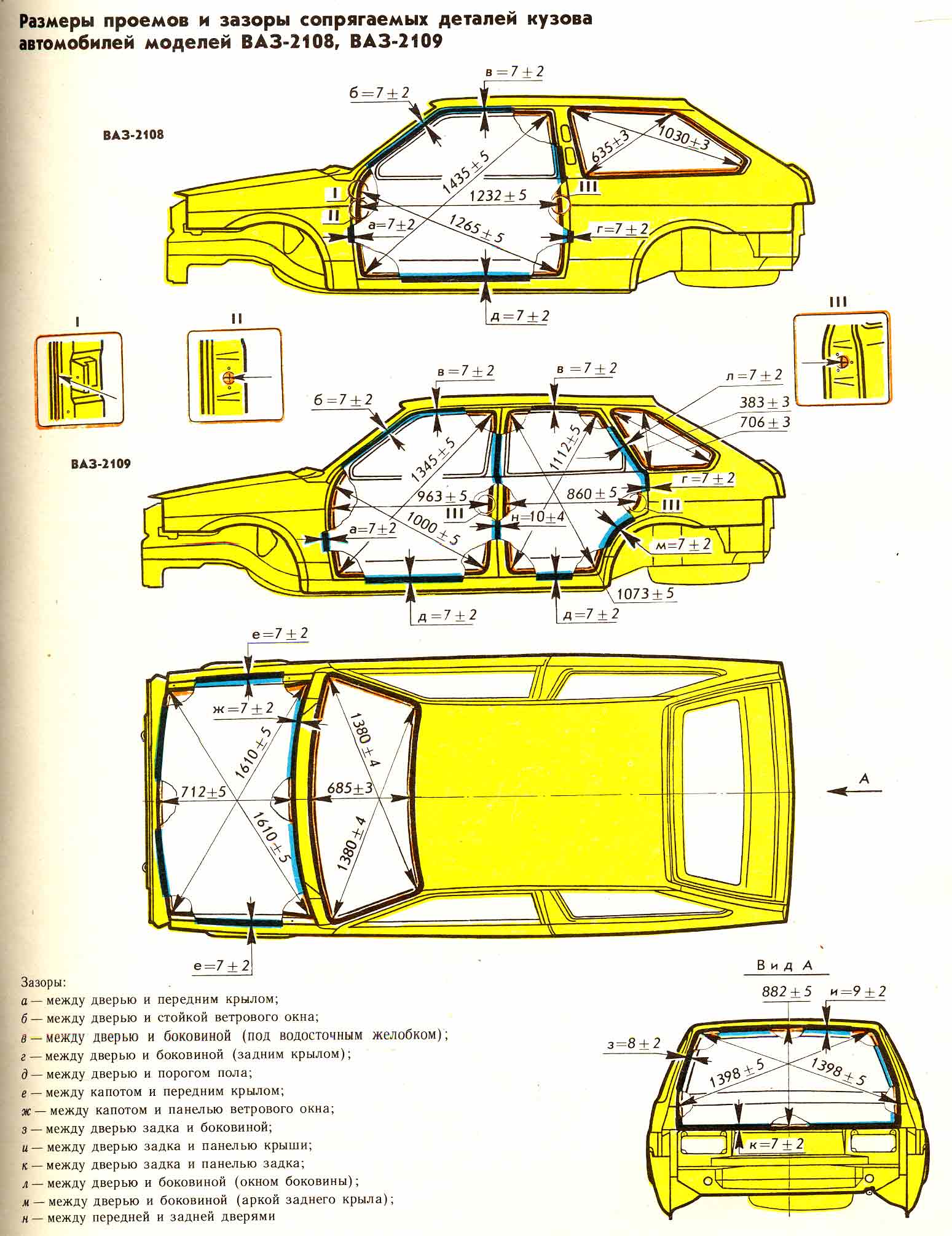 Даже незначительные изменения геометрии кузова способны спровоцировать серьёзнейшие проблемы. Если вы стремитесь, чтобы ваше транспортное средство обладало отличной маневренностью, характеризовалось безопасностью, тогда потрудитесь тщательно осмотреть автомобиль, проверить геометрию его кузова. У большинства автовладельцев может просто отсутствовать практика относительно того, как без специалистов проверить геометрию кузова. В таком случае эта информация будет весьма полезной.

Причины нарушения геометрии кузова

Сразу отметим, что не только дорожно-транспортные происшествия являются главными «виновниками» возникновения такой проблемы. Иногда симметричность нарушается именно по вине владельца транспортного средства или по независящим от него причинам.

В частности, если вам приходится эксплуатировать своё транспортное средство в плохих условиях, когда автомобилю приходится ежедневно преодолевать расстояния по бездорожью или по асфальтовому покрытию, которое «находится в неудовлетворительном состоянии, так называемые контрольные точки, постепенно смещаются, нарушая столь важную симметричность. Рекомендуется быть предельно внимательным, преодолевая незнакомую дорогу в условиях непогоды. Снег, дождь могут завуалировать опасные участки дорог, водитель на огромной скорости может влететь в огромную яму, наехать на большой камень. В качестве причины, по которой возникают нарушения геометрии кузова, может выступать неправильная «обувка» автомобиля. Если на одной подвеске будут использоваться разные шины, ждите скорой беды, устранение которой вам точно влетит в круглую «копеечку».

Суть геометрии кузова

Любое транспортное средство имеет так называемые контрольные точки. Измеряя расстояние между ними, можно сделать вывод, насколько правильно относительно друг друга расположены основные агрегаты, узлы, кузовные элементы. Чтобы понять, где конкретно находятся эти контрольные точки, нужно вооружиться технической документацией к транспортному средству. В ней автопроизводитель всё тщательно прописал. Чаще всего обращается внимание на расстояние между:

передней и задней колёсными базами;
лонжеронами.

Полезно измерить и соотнести:

ширину багажного и моторного отсека;
ширину колеи спереди и сзади;
размеры проёмов дверей и окон.

Первичный осмотр транспортного средства

Не спешите вооружаться инструментарием, закатывать рукава в момент первого «знакомства» с автомашиной, первичный осмотр может уже сразу указать на повреждения кузовных элементов, тогда не потребуется осуществлять каких-либо сложных вычислений, искать точки контроля, измерять расстояния между ними. Предлагаем провести совершенно несложную диагностику геометрии кузова. Начните с того, что просто откройте и закройте каждую дверь, капот и багажник. При полной исправности транспортного средства все эти элементы кузова должны с лёгкостью закрываться и открываться. Если же вам приходиться прилагать усилия для закрытия, например, дверцы, знайте, что у такого автомобиля искривлены стойки. Если же с усилиями закрываются и открываются багажник или капот, значит, можете быть уверенными в том, что искривлены лонжероны.

Теперь предлагаем вам присесть на корточки и внимательно посмотреть на кузов. Из такого нижнего положения вы легко заметите искривления. Полезно обратить внимание на стёкла спереди и сзади. Если на них вы заметили вертикальные трещины, это тоже может сигнализировать о смещении стоек. Опытные автомобилисты рекомендуют осуществлять проверку геометрии кузова автомобиля в процессе движения. Для проведения такого технического эксперимента вам понадобится дорога с хорошим покрытием.

Итак, разгоните транспортное средство до 50 км./ч., а затем отпустите руль. Внимательно пронаблюдайте в первые секунды, как поведёт себя автомобиль. Если он норовит уйти вправо или влево, значит, ему есть что скрывать. Это показывает, что автомобилю пришлось пережить аварию, в ходе которой удар пришёлся на ту сторону, в которую машину поведёт. Если же ваше авто продолжит ехать прямо, продолжите эксперимент, разгоните машину до 90 км./ч., вновь бросьте руль. Если и после такой повышенной скорости авто будет следовать прямо, можете прекратить проверку.

Проверка с использованием инструментария

Безусловно, для пущей убедительности можно даже в домашних условиях провести инструментальную проверку. Отлично, если в наличии имеется большой штангенциркуль. При помощи него измерьте расстояние между двумя контрольными точками, после этого зафиксируйте положение и перейдите к другим симметричным контрольным точкам. Если расстояние полностью совпадёт, всё в порядке, в противном случае, такое несовпадение указывает на деформацию кузова. Альтернативой штангенциркулю может выступать специальная линейка для точного измерения геометрии кузова. Принцип проверки идентичен, вам нужно, измеряя расстояния между контрольными точками, убедиться, что они одинаковы.

Проверка на СТО

Самой эффективной проверкой кузовной симметрии является определение целостности конструкции на станции технического обслуживания. Такая проверка находится вне конкуренции, поскольку на СТО в наличии имеется не только специальный инструментарий, но и эффективное современное компьютерное оборудование. Транспортное средство помещают на специальный стенд, к контрольным точкам подключают специальные датчики, благодаря которым вся информация поступает сразу на компьютер. Далее программное обеспечение сравнивает результаты полученных измерений с показателями, на которые ориентирует автопроизводитель. Безусловно, компьютерная проверка является максимально точной. Её единственным недостатком является тот факт, что за такую процедуру придётся платить. Не каждый автовладелец сможет раскошелиться, чтобы воспользоваться услугами компьютерной проверки.

Итак, проверка кузовной геометрии является одной из составляющих качественного технического обслуживания авто. Не жалейте времени и средств для проведения процедуры, а при приобретении авто с пробегом выполняйте её обязательно.

Проверка геометрии кузова авто по контрольным точкам: диагностика автомобиля.

Взаимное расположение ключевых точек автомобиля, зафиксированное в технической документации — именно так определяют специалисты геометрию автомобиля. Одной из главных причин изменения геометрии является ДТП, однако даже при повседневной безаварийной езде симметрия деталей кузова относительно друг друга может со временем меняться. Поэтому проводить соответствующую диагностику корпуса рекомендуется как минимум раз в год.

Нарушения сказываются на внешнем виде кузова, но главное в этой ситуации то, что неправильная геометрия влияет на безопасность водителя и пассажиров.

Причинами возникновения подобным проблем с кузовом являются:

Серьезные и мелкие ДТП
Езда по ухабам, ямам, разбитым проселочным дорогам
Наезд на бордюр и другие препятствия на дороге
Коррозия металла
Заводской брак
Износ кузова
Разные виды шины на колесах одной подвески
Превышение предельно допустимой массы автомобиля
Механические повреждения (упавшая ветка, камень, прыжок человека и т.д.)

Первые признаки нарушения геометрии автомобиля

Диагностика кузова необходима при покупке как подержанного, так и нового автомобиля. В первом случае необходимо выявить существующие повреждения, возникшие в процессе эксплуатации предыдущим владельцем авто. Отклонения от нормы могут свидетельствовать о том, что машина — битая. Во втором случае диагностика поможет выявить заводской брак. Разумеется, процедура требуется после любого ДТП и в том случае, если вы заметили следующие признаки:

Машину «ведет» во время езды, в салоне чувствуется вибрация, авто хуже случается руля;
Между конструктивными деталями кузова есть большие или несимметричные зазоры и щели;
Двери стали плохо закрываться, слышен скрип, замки срабатывают с трудом;
Хуже открываются и закрываются багажник и капот
Увеличился расход топлива без видимой причины
Увеличился износ резины
В салоне слышны посторонние звуки, стук подвески, скрипы и шумы

Нарушения геометрии должны устраняться сразу при выявлении. Дальнейшая эксплуатация автомобиля с искривленным кузовом только усилит деформацию, и затраты на комплексное восстановление машины вырастут в разы.

Стоит ли проверять геометрию авто самостоятельно?

Проверка кузова начинается с визуального осмотра всех лицевых панелей, швов, стыков, а также днища машины – при помощи подъёмника. Все это можно сделать и в обычном гараже, однако для дальнейшей проверки потребуется специализированное высокоточное оборудование, которое вряд ли имеется в распоряжении рядового автовладельца.

С помощью современных инструментов диагностики мастера «АвтосервисПрофи» в Калининграде проводят замеры ширины задней и передней колеи, длины лонжеронов и расстояния между ними, а также диагоналей дверных проемов.

После этого машину подвергают проверке контрольных точек. Осуществляется она с помощью специальных электронных датчиков, которые крепятся в указанных местах в соответствии с инструкцией от завода изготовителя. После этого специалист проверяет соответствие реального положения контрольных точек указанным в документации расстояниям.

Если выявлена деформация, ее устраняют на стапеле. Машину вытягивают специальными приспособлениями, работа которых контролируется компьютером. Современные технологии, которые используются в компании «АвтосервисПрофи», позволяют полностью исправить даже минимальные погрешности и искривления.

Как проверить геометрию кузова автомобиля

Покупая подержанную машину, необходимо убедиться в том, что геометрия ее кузова не нарушена. Возникнуть подобное может из-за серьезной аварии. А это может негативно сказаться на ухудшении эксплуатационных качеств авто, на его безопасности и ухудшении управляемости.

Как самому осуществить проверку геометрии кузова

1. Закройте двери автомобиля, крышку багажника и капота. Обратите внимание, с какой силой они закрываются. Если при закрывании хотя бы одной двери либо крышки нужно приложить усилия, то это говорит о нарушении геометрии. Если плохо закрывается дверь, то причиной этому может стать повреждение стоек.

2. Если на лобовом стекле есть горизонтальные трещины, они также могут говорить о проблемах с геометрией кузова.

3. Тщательно осмотрите кузов автомобиля. Если между дверями и крышками багажника и капота ширина зазора отличается, то это также явный признак нарушения геометрии.

Как рулеткой проверить геометрию кузова

Начинаем с проверки передней колеи: для этого необходимо замерить длину от центральной части протектора переднего колеса с левой стороны до центральной части протектора переднего колеса с правой стороны. Затем аналогичным способом осуществляем проверку задней колеи. После чего проверяем полученные данные со сведениями завода производителя. Если данные совпадают, то с машиной все в порядке. Если есть расхождения, то, соответственно, геометрия нарушена.

Таким же методом осуществляем проверку длины колёсной базы. Делаем это таким образом: замеряем между центральной частью ступицы переднего колеса и центральной частью ступицы заднего колеса – данные должны совпадать.

Проверить геометрию можно и другим более простым методом:

Разгонитесь на машине по прямой ровной асфальтированной дороге, после чего отпустите руль буквально на несколько секунд. Если автомобиль станет уводить в сторону, то не исключено, что геометрия нарушена. Проверяем автомобиль на разных скоростях — 50 и 90 километров в час.

О чем ещё необходимо помнить

Если при осмотре не было обнаружено явных нарушений геометрии кузова, то это ещё не даёт стопроцентной гарантии. Возможно, автомобиль был хорошо отремонтирован. Но каким бы качественным не был ремонт, автомобиль уже не будет таким же надёжным и безопасным. И чтобы полностью развеять все сомнения, пробейте авто по ВИН-коду. Для проверки существует множество сервисов в интернете. Заходим на сайт и вбиваем номер, после чего система выдает результат. Если автомобиль был в аварии, то информация о ДТП будет доступна. В частности вы узнаете, тип аварии и схему повреждения.

Проверка геометрии кузова

Диагностика геометрии необходима не только для восстановления кузова при проведении крупного кузовного ремонта, или для контрольных замеров автомобилей проходящих кузовной ремонт — но и для проверки покупаемого подержанного автомобиля.

Даже небольшой удар, нанесенный Вашему автомобилю по касательной траектории способен на несколько микронов изменить геометрию кузова.

В этом случае Вы, произведя ремонт только поврежденной детали, через некоторое время заметите, что износ покрышек происходит быстрее, чем раньше, а регламентные работы по подвеске требуют все больше внимания специалистов.

Предварительное измерение геометрии кузова избавит от вышеперечисленных неприятностей и позволит избежать дополнительных расходов.

Проверка геометрии кузова автомобиля — очень востребованная услуга в нашем техцентре. Стоит она не дорого, зато пользу приносит огромную.

Что же ощущает водитель и какие последствия ожидает автомобиль, геометрия кузова которого нарушена?

Ну, во-первых, о комфортной «езде с ветерком» придется забыть – на скорости, превышающей 80 км/час, автомобиль начинает вибрировать, он становится плохо управляем, превращая управление автомобилем в кошмар.

Во-вторых, резко повышается износ резины, элементы подвески начинают напоминать о себе постукиванием и поскрипывание гораздо чаще, растет расход бензина. Все это ведет к дополнительным финансовым издержкам.

Основные последствия нарушения геометрии автомобиля:

нарушение симметрии колес автомобиля (первые признаки – повышенный износ шин и плохая устойчивость автомобиля при движении)
нарушение диагоналей кузова (контрольных точек). Такие точки заданы в геометрии кузова конструктивно на заводе изготовителе. Проводятся они под остовом кузова между определенными точками рамы или элементов подвески (если конструктивно автомобиль безрамной конструкции). Искажение диагоналей также можно наблюдать и в других частях – рамках переднего или заднего стекла, проемов дверей.
деформации кузова (изменение геометрии) сопровождаются образованием складок днища или другого элемента основания или рамы.

Проверка геометрии кузова автомобиля позволяет выявить смещения не только на кузове, но и на раме внедорожника.

Если Вы купили автомобиль — а он оказался с поврежденным кузовом, или Вы случайно попали в ДТП, после которого машина изменила свои конструктивные размеры, приезжайте в ТЦ «Ремонт рам».

Мы проверим геометрию кузова и вместе с Вами найдем самый лучший способ исправить имеющуюся проблему.

А еще — запишите наш номер: +7 (495) 775-86-65 себе в мобильный телефон и при любой покупке или обмене автомобиля, приезжайте к нам. Мы позаботимся, чтобы Вы случайно не приобрели себе «кота в мешке».

Создание новой детали путем копирования геометрии тела

Урок 5: Создание новой детали путем копирования геометрии тела

В этом уроке вы создадите новую деталь из тела. Затем вы обновляете исходную деталь и смотрите, как это повлияет на новую деталь.

• Рекомендуется последовательно выполнять упражнения в течение одного сеанса Creo Parametric.

• В следующих упражнениях вам будет предложено использовать команды с ленты. После выбора элементов вы также можете получить доступ к этим командам с мини-панели инструментов или щелкнув правой кнопкой мыши.

• В видеороликах с упражнениями для выхода из инструмента во многих случаях использовался средний щелчок.

Это руководство разделено на 5 упражнений, чтобы упростить выполнение:

Упражнение 1: Возобновление подавленных функций

Посмотрите видео, демонстрирующее шаги этого и следующего упражнений:

1.Установите рабочий каталог на tutorial5. и откройте clip_master.prt.

2. Щелкните и снимите флажок (Выбрать все), чтобы отключить отображение датума в графическом окне.

3. В дереве модели перетащите зеленый индикатор под двумя последними элементами.

На этом завершается первое из 5 упражнений.

Упражнение 2: Разделение тела на 2 тела

1. Разверните папку Bodies в дереве модели и выберите PIECE1.

2. Щелкните Разделить тело. Откроется вкладка Разделить тело 3. Щелкните Громкость.

4. Выберите поверхность, которая принадлежит одному объему, как показано на следующем рисунке.

5. Щелкните.

6. Дважды щелкните новое тело, введите имя piece2 и нажмите ENTER.

7. Выберите ЧАСТЬ2 кузова.

8. Щелкните Просмотр.

9. Щелкните стрелку под заголовком «Внешний вид» и щелкните зеленый кружок, как показано на следующем рисунке.

10. PIECE2 изменится на зеленый.

11. Щелкните Модель, чтобы вернуться на вкладку Модель.

12. Выберите тело PIECE2, щелкните правой кнопкой мыши и выберите Параметры.Откроется диалоговое окно «Параметры».

13. Щелкните. В список параметров добавлен новый параметр.

14. Назовите параметр piece_num.

15. Щелкните поле Тип и измените тип на Целое число.

16. Щелкните поле Value и введите 2.

17. Щелкните OK.

На этом мы завершаем второе из 5 упражнений.

Упражнение 3: Создание новой детали из тела PIECE1

В этом упражнении новая деталь создается как элемент «Копировать геометрию» тела. Параметры и свойства исходного тела копируются вместе с деталью.После создания детали вы устанавливаете параметры управления обновлением, чтобы определить, как и будет ли обновляться деталь при изменении исходного тела.

Посмотрите видео, демонстрирующее шаги этого упражнения:

1. В дереве модели выберите PIECE1, щелкните правой кнопкой мыши и выберите «Создать деталь из тела». Откроется диалоговое окно «Новая деталь из тела».

2. Введите новое имя файла, clamp_p1.

3. Щелкните OK. Новая деталь, CLAMP_P1, откроется в графическом окне. Обратите внимание, что единственная функция в дереве модели — это внешняя функция Copy Geom.

4. Разверните папку «Тела». Обратите внимание, что название тела — PIECE1.

5. Выберите тело PIECE1, щелкните правой кнопкой мыши и выберите Параметры. Откроется диалоговое окно «Параметры». Обратите внимание, что параметр PIECE_NUM имеет значение 1.

6. Щелкните OK.

7. Щелкните правой кнопкой мыши элемент extern Copy Geom и выберите. Откроется вкладка «Копировать геометрию».

8. Щелкните Параметры.

9. Выберите «Обновление вручную» и установите флажок «Уведомлять».

10. Щелкните.

На этом завершается третье из 5 упражнений.

Упражнение 4: Создание новой детали из тела PIECE2

Посмотрите видео, демонстрирующее шаги этого упражнения:

1. Вернитесь в окно детали CLAMP_MASTER.

Щелкните стрелку рядом с панелью быстрого доступа, чтобы выбрать другое окно.

2. Выберите PIECE2, щелкните правой кнопкой мыши и выберите «Создать деталь из тела». Откроется диалоговое окно «Новая деталь из тела».

3. Введите новое имя файла, clamp_p2.

4.Щелкните ОК. Новая деталь, CLAMP_P2, откроется в графическом окне. Обратите внимание, что единственная функция в дереве модели — это внешняя функция Copy Geom.

5. Разверните папку «Тела». Обратите внимание, что название тела — PIECE2.

6. Выберите тело PIECE2, щелкните правой кнопкой мыши и выберите Параметры. Откроется диалоговое окно «Параметры». Обратите внимание, что параметр PIECE_NUM имеет значение 2.

7. Щелкните OK.

8. Щелкните правой кнопкой мыши функцию extern Copy Geom и выберите Update Control, обратите внимание, что выбрано автоматическое обновление.

На этом завершается четвертое из 5 упражнений.

Упражнение 5: Создание скруглений

Посмотрите видео, демонстрирующее шаги в этом упражнении:

1. Вернитесь в окно детали CLAMP_MASTER.

2. Перетащите зеленый индикатор внизу дерева модели над выдавливанием 1.

3. Выберите нижний край детали и нажмите «Скруглить». Откроется вкладка Round.

4. Выберите верхнюю кромку детали и установите радиус скругления равным 1,00.

5. Щелкните.

6. Перетащите зеленый индикатор в нижнюю часть дерева модели. Обновлена деталь с двумя телами и добавлены патроны.

7. Вернитесь к части CLAMP_P1. Обратите внимание, что функция extern Copy Geom имеет желтый треугольник, что означает устаревшую функцию. Эта часть была настроена на ручное обновление с уведомлением.

8. Выберите элемент в дереве модели, щелкните правой кнопкой мыши и выберите>. На обновленной части появляются раунды.

9. Вернитесь к части CLAMP_P2.

10. Щелкните на панели инструментов быстрого доступа или под графическим окном.Деталь восстанавливается, и появляются патроны. Эта часть была настроена на автоматическое обновление.

На этом завершается урок 5.

Представление твердотельной геометрии — MATLAB и Simulink

Геометрия в модели

Геометрия является ключевым атрибутом твердых тел и тел, которые они составляют. Это функции в твердых визуализациях, предоставляемых твердотельными блоками в качестве наглядных пособий во время моделирование. Он также присутствует в многотельных визуализациях, отображаемых в Mechanics Explorer после сборки модели и во время моделирования.Это одна цель твердотельной геометрии: обеспечить визуализацию всего рабочий процесс моделирования, от концепции отдельного твердого тела до моделирования полной многотельной модели.

Геометрия элемента тела

Сплошная геометрия служит второй, менее заметной цели: упрощение спецификации инерция в твердых блоках. Основная часть инерционных параметров твердых тел: легко вычисляется, если и геометрия, и масса, или, альтернативно, массовая плотность, известны.Сплошные блоки обеспечивают параметризацию инерции, Вычислить из геометрии , которая выполняет эти расчеты для вас. Вы указываете твердотельную геометрию и меру ее масса; блок выполняет необходимые численные интегрирования для получения остальные инерционные параметры — моменты инерции, произведения инерция и центр масс.

Геометрия в блоках элементов тела

Твердотельная геометрия на практике отличается от рам и инерции.В последние — это атрибуты, которые можно моделировать изолированно, используя такие блоки, как как жесткое преобразование и Инерция. Здесь нет эквивалентный специальный блок для твердотельной геометрии. Блоки Graphic и Spline представляют геометрию — и предоставить средства визуализации для этих геометрических фигур, но ни то, ни другое адекватная замена реальной твердотельной геометрии.

Графический блок просто добавляет маркер к кадру, обычно как средство выделения этого кадра.В Блок сплайна добавляет плоскость или пространство curve в основном предназначена для использования с блоком Point on Curve Constraint. Если хотите визуализировать твердые тела и тела или воспользоваться автоматической инерцией расчеты, которые позволяет твердотельная геометрия, вы должны использовать твердотельную блокировать.

Упражнение: укажите простую цилиндрическую форму

Используйте блок Cylindrical Solid для смоделировать тело простой заданной формы — цилиндр радиусом 5 см. и длиной 20 см.Визуализируйте твердое тело на панели визуализации Блок Cylindrical Solid. Игнорировать относительное размещение твердого тела в (неполной) модели.

Добавить цилиндрическое тело block к новой модели Simulink и откройте диалоговое окно блока. Обратите внимание на раздел параметров Geometry , который по умолчанию определяет форму цилиндра 1 м в боковая сторона.
В строке параметра Radius введите значение 5 и выберите единицы см .Вы можете выбрать свои единицы из раскрывающегося списка или введите их вручную.
В строке параметра Длина введите значение 20 и снова выберите единицы измерения см . Обратите внимание на предупреждение в панель визуализации, предлагающая обновить твердое тело визуализация.
На панели инструментов визуализации щелкните значок Обновить визуализацию кнопка. В панель визуализации обновляется с новой твердотельной геометрией но из-за небольших размеров его почти не видно.Нажмите кнопку Fit to View , чтобы оптимизировать уровень масштабирования. Убедитесь, что твердотельная геометрия как и ожидалось.
Разверните раздел параметров Inertia и обратите внимание на параметр Тип параметр. Автоматический расчет инерционных свойств из геометрии по умолчанию включен. Завершить модель твердого тела, вам нужно только убедиться, что его масса или масса плотность установлена на правильное значение.Нажмите ОК , чтобы принять текущее твердое тело настройки.

Размещение и ориентация твердого тела в модели

Если твердотельный блок не соединен, относительное размещение этого твердого тела не определено. К решить твердую позу — ее положение и ориентацию — в модели, вы должны подключите порт опорного кадра ( B ) или, если хотите, порт настраиваемого фрейма, принадлежащий сплошному блоку. Например, подключение порта R к порт мира W Блок кадра выровнял бы твердое тело так, чтобы его система отсчета совпадает с мировой системой отсчета.На рисунке показано такое соединение

Определение пространственных отношений, таких как это, является ключом к моделированию в среда Simscape Multibody. Вы можете вращать и переводить два фреймов по отношению друг к другу, применяя операции, называемые жестко преобразует между этими кадрами. Учить подробнее о фреймах и преобразованиях см. Работа с фреймами.

Для простоты моделирования твердые блоки предоставляют интерфейс для создания фреймов.Вы можете использовать этот интерфейс для добавления и выравнивания новых кадров для выбора геометрии объекты, такие как вершины, ребра, грани и объемы. Чтобы узнать, как Создание рамок с помощью этого интерфейса см. в разделе «Создание пользовательских сплошных рамок».

Предустановленные твердые формы

Сплошные блоки предоставляют большой набор предустановленных форм — те, которые имеют простые параметризации с легко доступными параметрами, такими как Радиус и Длина в качестве входных данных. Предустановленные формы позволяют быстро моделировать сферические, цилиндрические и призматические твердые тела, среди прочего.Для большей универсальности предварительно заданные формы включить экструдированный Сплошной блок и вращающийся Сплошной блок — формы, поперечные сечения которых, будь они вдоль или относительно оси, вы можете изменить. Чтобы узнать больше об этих формах, см. Моделирование выдавливаний и революций.

Упражнение: укажите простую вращающуюся форму

Используйте блок Revolved Solid для моделирования твердое тело вращения — конус высотой 5 футов и радиусом основания также 5 футов. Визуализируйте твердое тело на панели визуализации Вращающийся твердый блок.Игнорировать относительное размещение твердого тела в (еще не завершенной) модели.

Добавить твердотельный блок Revolution в модель Simulink.
В строке параметра Поперечное сечение , введите матрицу координат [0 0; 5 0; 0 5] и выберите единицы футов . Каждая матрица строка обеспечивает [ x z ] пара координат, заданная в указанном порядке, для точки сечения.
Нажмите кнопку Обновить визуализацию и кнопку Fit to View . Гарантировать, что сплошная геометрия такая, как ожидалось. Нажмите OK для принятия новой твердотельной геометрии и закройте диалоговое окно блока.

Задание твердых сечений

Блок Revolved Solid генерирует вращающуюся форму с помощью подметание указанного поперечного сечения xz около ось z.Чтобы последовательно создавать правильную форму без ошибок, Вращающийся твердый блок усиливает несколько правила. Прежде всего, это требование, чтобы по мере того, как вы исходили из одна точка в координатной матрице к следующей, сплошная область лежит слева и пустая (или пустая) область справа. То же правило применяется к экструдированным формам с одним отличием: поперечное сечение координаты ( x , y ) пары и поперечное сечение лежит в плоскости xy .

Imported Solid Shapes

В качестве альтернативы вы можете использовать блок File Solid для импортировать твердое тело из файла внешней геометрии. Файл Твердые блоки позволяют создавать твердые тела со сложными геометрии. В настоящее время блок File Solid поддерживает форматы STEP (также называемые STP) и STL.

Формат STEP рекомендуется, поскольку он приводит к тому, что обычно меньше файлов, чем эквивалентная геометрия STL. ШАГ также единственный из двух форматы, позволяющие автоматически рассчитывать инерцию по геометрии.Ты должны явно указывать моменты инерции, продукты инерции и центр масс твердого тела при импорте геометрии STL.

Обратите внимание, что очень большие файлы могут загружаться медленно и задерживать обычно быстрый этап обновления модели. (на вкладке Modeling нажмите Update Модель ). Размер файла STEP или STL в некоторой степени зависит от в приложении, использованном для создания файла. В некоторых случаях можно уменьшить размер, используя другое приложение для экспорта твердотельной геометрии.

Упражнение: импорт файла геометрии STEP

Используйте блок File Solid для импорта детального конического зубчатого колеса геометрия. Геометрия шестерни была создана в программном обеспечении САПР, а затем экспортируется в формате STEP. Визуализируйте твердое тело на панели визуализации блока Solid и игнорируйте относительное размещение тела в модели.

Добавить блок File Solid в Модель Simulink.
Раздел параметров Geometry обновления, чтобы показать необходимый импорт файла свойства — Тип файла , Имя файла , и только для файлов STL, Единицы .
Из раскрывающегося списка Тип файла , выберите ШАГ . Это рекомендуемый тип файла геометрии. Файлы STEP обычно меньше, чем их аналоги в STL, и позволяют автоматически расчет по геометрии.
В поле параметра Имя файла введите bevel_c.step . Это имя файла соответствует примерной геометрии STEP, которая по умолчанию на вашем пути MATLAB.Если у вас возникнут проблемы, вы можете введите файл путь:
```
  matlabroot  /toolbox/physmod/sm/docexamples/bevel_gear/bevel_c.step 
```
где matlabroot — корневая папка вашего Установка MATLAB. Если вы не уверены в местонахождении ваша корневая папка, в командной строке MATLAB введите matlabroot .
Щелкните значок обновления визуализации кнопку, а затем Fit to View кнопка.Убедитесь, что твердотельная геометрия соответствует ожиданиям. Нажмите ОК принять новое твердое тело геометрии и закройте диалоговое окно блока.

Получение файлов твердотельной геометрии

Из модели САПР можно получить файл геометрии в формате STEP или STL. Большинство приложений САПР позволяют экспортировать геометрию деталей в эти (среди прочего) форматы. Если у вас есть опыт работы с приложениями САПР или у вас есть поддержка кого-то, кто есть, вы можете создать подробную твердую геометрию в CAD, экспортируйте его в файл STEP или STL и импортируйте окончательный файл геометрии. в блок File Solid.

Если у вас нет лицензии на профессиональное приложение САПР, с открытым исходным кодом программное обеспечение, такое как FreeCAD, может предоставить подходящую альтернативу. Оншейп, а профессиональное полностью облачное приложение САПР с бесплатной подпиской планы. Преимущество этого инструмента в том, что он позволяет импортировать полные многотельные сборки в среду Simscape Multibody с помощью smexportonshape функция. Для дополнительной информации, см. Импорт Onshape.

Составные твердотельные формы

Если вы не можете получить файл STEP или STL с требуемой твердотельной геометрией, вы по-прежнему можете аппроксимировать эту геометрию, комбинируя более простые предустановленные формы в более крупную сложную форму.Вы должны использовать несколько твердотельных блоков — один для каждая предустановленная сплошная форма. Часто необходимо также использовать Rigid Блоки преобразования, чтобы указать пространственные отношения которые существуют между твердыми системами отсчета. На рисунке показан сплошной геометрия, которую можно смоделировать как составную фигуру — бинарную связь с отверстием секция (обозначена A ), основная секция ( B ) и секцию под штифт ( C ).

Пример, показывающий, как моделировать это составное тело, см. В разделе «Упражнение: создание составной геометрии».

Геометрия анатомии | интенсион дизайнов

авторское право T. Flemons 2007

Среди клиницистов и специалистов по телу сегодня, похоже, есть большой интерес к концепции тенсегрити применительно к живым формам, но также и много путаницы. В некоторых кругах это кажется ароматом десятилетия, но о чем они говорят? Что такое тенсегрити? Является ли это полезным научным описанием и объяснением анатомической функции? Или это просто метафора интуитивного ощущения, что тела ведут себя как целые системы, находящиеся в соединительном напряжении? В последнем случае это так же хорошо или лучше, чем любая другая аналогия, и определение может оставаться расплывчатым.Но если тенсегрити утверждает, что объясняет биомеханику живой структуры, то требуется больше. Требуется четкое определение «биотенсегрити» и средства для проверки гипотезы. Необходимо изучить фактические отношения между компонентами растяжения и сжатия в теле. Может ли биотенсегрити объяснить сложное взаимодействие этих сил с точки зрения биомеханики, и если да, то что это означает? Одним из признаков действительной научной гипотезы является ее предсказуемость. Если тенсегрити дает лучшее описание, значит ли это для лучших рецептов?

Я не анатом, биомеханик или кузовщик.Я пришел к этой работе как геометр со свежим взглядом и новыми идеями. Я делаю напряжение для жизни и для удовольствия — игрушки, мебель, скульптуры, мобильные устройства и биотермогрити, и всегда в центре внимания то, как что-то построено. Обращаю внимание на детали. В случае живых существ я попытался применить то, что я узнал о геометрии структуры, по сути, для обратного инжиниринга эволюции. Я ищу наиболее эффективную с точки зрения материалов и энергопотребления стратегию для организации и разработки самосборных, прочных, отказоустойчивых, ремонтопригодных, гибких и легких мобильных каркасов.

Довольно сложно, но, говоря таким образом, я могу сосредоточиться на геометрии тела и предположить, как и если оно состоит из паттернов, идентифицируемых как tensegrities.

Мои модели тенсегрити — это абстракции тела, разработанные для приблизительной схемы сил и движений, действующих на анатомическую структуру. В поисках близкого соответствия по форме и функциям я попытался смоделировать человеческую форму и функции, используя только этот принцип. Спустя много итераций я все еще проверяю гипотезу.

Рис. 1. Скелет Тенсегрити.

Геометрия Тенсегрити — это язык, который я использовал для интерпретации и представления анатомической формы как динамического взаимодействия сил в четырех измерениях (тела, движущиеся во времени). То, что я обнаружил, интригует — движение и степени свободы в моделях кажутся примерно аналогичными человеческому движению и свободе. Кроме того, изменения в одной части модели (например, локальное повышенное напряжение) отражаются по всей конструкции; это похоже на наблюдение, что боль в теле часто возникает на расстоянии от источника оскорбления.Это наводит на размышления, но это не доказательство. В данной статье делается попытка приступить к проработке деталей теории.

Тенсегрити — это…

Tensegrities — это напряжение и сжатие. Каждая структура, будь то артефакт, созданный разумом, или живая форма, возникшая в результате естественного отбора, представляет собой баланс между этими двумя и только этими двумя силами. Инженер и архитектор Марио Сальвадори указывает в своей книге Почему здания стоят, , что сдвиг эквивалентен силам растяжения и сжатия, действующим под прямым углом, и не является отдельной силой.¹ Tensegrities — это особые конструкции, в которых игра этих двух сил видна в конструкции.

Но тенсегрити, безусловно, один из самых мощных мемов в современную эпоху. Я думаю, это из-за элегантности и мощи тенсегритизма, необходимой для описания и иллюстрации поведения целых систем как фракталов. Тенсегрити — мощная метафора для синкретического и неатомистического представления о существовании. Он приобрел множество значений на многих уровнях полового акта…

Карлос Кастанеда присвоил этот термин как… «Название, данное современной версии магических пассов: положения и движения тела и дыхания, о которых мечтали и преследовали мужчины и женщины-провидцы, жившие в Мексике в древние времена…» 2 Выяснилось, что Кастанеда восхищался Р.Бакминстер Фуллер, придумавший термин; Затем он позаимствовал это слово и приобрел авторское право для своих целей.

Канадский теоретик Стаффорд Бир, основатель кибернетики управления, также восхищался Фуллером и использовал тенсегрити как социальную метафору для описания сложных взаимоотношений, связанных с принятием решений в группах. Он ввел термин «синтегрити», поскольку тенсегрити уже был защищен авторским правом…

Википедия взвешивает: «Тенсегрити — это сумочка целостности напряжения. Это относится к целостности конструкций, основанной на синергии между сбалансированными компонентами растяжения и сжатия.² Синергия относится к наблюдению, сделанному первым Р. Бакминстером Фуллером, что в любой системе целое всегда больше суммы его частей. Поведение тенсегрити — наглядная демонстрация этого.

Как это определяет Фуллер? Из Synergetics 700.011: «Слово тенсегрити — изобретение: это сокращение целостности натяжения. Тенсегрити описывает принцип структурных отношений, в котором структурная форма гарантируется конечно замкнутым, всесторонне непрерывным, растягивающим поведением системы, а не прерывистым и исключительно локальным поведением элементов сжатия.³ Ему легко сказать… Фуллер продолжил проектировать самые большие закрытые купола, когда-либо построенные, используя принципы тенсегрити.

Скульптор Кеннет Снельсон, создавший первые структуры тенсегрити в 1948 году, назвал их чем-то другим. В интервью он сказал: «Слово тенсегрити стало настолько запутанным из-за множества употреблений, что ставит под сомнение любое определение. Это причина, по которой я долгое время выступал за плавающее сжатие … (Он) описывает замкнутую конструктивную систему, состоящую из трех или более удлиненных стоек сжатия внутри сети растянутых арматурных элементов, при этом комбинированные части поддерживают друг друга таким образом, что стойки не касаются друг друга, а прижимаются наружу к узловым точкам в сети натяжения, чтобы сформировать прочный, треугольный, предварительно напряженный узел растяжения и сжатия.Почему триангулированы? Причина в том, что можно построить такую структуру, сеть которой не является триангулированной. Такие структуры вялые и явно не твердые ». ⁴ В мире искусства Снельсон хорошо известен, и его плавающие компрессионные скульптуры можно найти в галереях, частных коллекциях и музеях по всему миру. (http://www.kennethsnelson.net/faqs/faq.html)

Тенсегрити требует как минимум трех условий, чтобы соответствовать определению Кеннета Снельсона или Бакминстера Фуллера.

1. Непрерывная соединительная растянутая сеть поддерживает прерывистые компрессионные стойки. Снельсон настаивает на том, что стойки должны свободно плавать в натянутой паутине и не касаться друг друга. Геодезический купол, который Фуллер считает напряженным, имеет несколько стоек сжатия, встречающихся в центральных узлах, но они соединены прерывисто, то есть они не переносят сжимающие нагрузки. В этих куполах непрерывно действуют силы натяжения, которые проходят по внешним краям стоек.Точно так же, если анатомические структуры действуют как тенсегриты, то в большинстве ориентаций кости не передают прямую нагрузку через сустав — скорее, элементы растяжения; связки, сухожилия и фасции переносят нагрузки, а кости плавают в этой матрице напряжения.

2) Все напряжения предварительно напряжены под напряжением; они самоподдерживаются и не зависят от силы тяжести. Но вес конструкции также увеличивает предварительное напряжение. По мере увеличения веса нагрузки тенсегрити сужается и становится меньше.Чем тяжелее конструкция, тем больше напряжение и меньше диапазон движений. Это создает реальные проблемы проектирования при попытке моделирования живых систем, которые имеют и используют суставы с несколькими степенями свободы. Мои модели, например, могут имитировать биологическое движение, потому что я использую эластичные натяжные сети, которые достаточно натянуты, чтобы сохранять форму модели, но при этом обладают достаточной остаточной эластичностью для перемещения в широком диапазоне положений. Когда размер и вес модели увеличиваются, увеличивается и предварительное напряжение.Всегда удивительно обнаруживать, насколько высок уровень напряжения при строительстве больших конструкций тенсегрити. В некоторых из самых больших скульптур Снельсона (50–100 футов) натяжные тросы несут в себе силы в тысячи фунтов. Создать модели тенсегрити в человеческом масштабе, которые четко формулируются и предварительно напряжены, — нетривиальная задача.

3) Tensegrities — это автономные, не дублирующие целые системы. Все компоненты динамически связаны, так что силы переводятся повсюду мгновенно; изменение одной части отражается повсюду.Эти особенности отличают tensegrities от всех других структур натяжения, например Радиомачта или мачта парусника закреплены на основании и нуждаются в этой фиксированной точке, чтобы держать его в вертикальном положении. Лодке не нужна мачта для ее целостности, но обратное неверно. Каждая часть тенсегрити зависит от всей структуры для ее непрерывного существования. С точки зрения живых форм, разрыв в структуре отмечает границу или границу между отдельными напряжениями. Кроме того, молекулы внутри клеток внутри тканей внутри органов внутри тел и тела внутри окружающей среды — все синергетически связанные напряженности в иерархическом каскаде от мельчайших целых к самым большим.

В макромасштабе анатомии человека я рассматриваю тенсегрити как схематический способ моделирования в четырех измерениях сил, действующих на сложные формы, в терминах векторов напряжений. Я предполагаю, что этот аналитический метод может объяснить структуру отдельных костей, а также совокупностей, составляющих тело. В этом смысле тенсегрити — это прикладной принцип — карта природы структуры. Если тенсегрити рассматривать не столько как строительную систему, сколько как описание наиболее эффективного способа организации всех форм с точки зрения наиболее экономичного использования энергии и материалов, то мы ожидаем, что бережливая природа будет использовать этот принцип повсеместно.Задача состоит в том, чтобы точно определить, как это могло быть достигнуто в каждом масштабе континуума.

Биотенсегрити

За последние 25 лет тенсегрити стал ассоциироваться с различными исследованиями природы живой структуры. Дональд Э. Ингбер, доктор медицинских наук, профессор патологии Гарвардской медицинской школы, провел исследования клеток, которые широко освещались в крупных научных журналах, а также в журнале Scientific American, The Architecture of Life , январь 1998 г.Он нашел убедительные доказательства того, что тенсегрити является лучшим объяснением цитоскелета клетки, ее движения и поведения. Стивен Левин, хирург-ортопед, который ввел термин биотенсегрити, применял этот принцип к анатомии на макроуровне в своих статьях и многочисленных лекциях по всему миру на протяжении более 25 лет. Его видение биомеханической биотенсегрити радикально и всесторонне. (biotensegrity.com). Другие, такие как Том Майерс, известный писатель и преподаватель структурной интеграции (http: // www.anatomytrains.us/), а также Джордж Рот, писатель и мануальный терапевт из Торонто (http://www.matrixinstitute.net/), оба используют этот термин, помогая объяснить свою практику и методологию, но используется общий и в основном метафорический. На эту тему пишут многие, но не все понимают тенсегрити одинаково. А некоторые ясно понимают меньше…

В статье для остеопатического журнала американский остеопат использовал тенсегрити для моделирования черепно-сакральной работы, но назвал изображение эстакады поезда примером тенсегрити.Козловой мост представляет собой открытый каркас со связями — ферму, которая передает силы на землю через сжимающие элементы — это не позволяет использовать ее как тенсегрити. Физиотерапевт, интересовавшийся этой концепцией, думал, что паутина представляет собой структуру тенсегрити. Но паутина устроена так же, как батут — гибкая натяжная мембрана, подвешенная к внешнему каркасу, который не зависит от мембраны. Ветвь не полагается на Интернет для поддержки, но Интернету нужна ветка. Индивидуальные напряженности являются неотъемлемой частью — все части связаны неиерархическими отношениями.Курильщик, использующий тенсегрити как метафору, сравнивает его с мачтой в парусной лодке. Но судовая мачта действует как рычаг, точкой опоры которого является палуба лодки (целостность которой не зависит от мачты), и ей препятствуют наклоны натяжных кожухов. У тенсегритов нет рычагов или опор в классическом смысле. Силы передаются глобально по всей структуре. Известный учитель учителей йоги, которая говорит о тенсегрити в своем наставлении, думала, что она живет в доме тенсегрити, потому что у него треугольные секции крыши.Несомненно, у нее устойчивая крыша, но это не тенсегрити. Каждый из этих врачей использовал тенсегрити в качестве аналогии, основанной на структурах напряжения или стабильности через триангуляцию, для описания своей работы, но никто не использует этот термин правильно. Все тенсегрити-структуры являются растягивающими, но не все растягивающие конструкции тенсегрити. Поскольку мы связаны вместе соединительной тканью, которая действует в напряжении, законно спросить, что это за форма растяжения.

Геометрия тенсегрити

Учитель йоги был частично прав; речь идет о треугольниках.Единственный способ полностью стабилизировать и ограничить любую конструкцию — это триангулировать поверхности или полости при сжатии и / или растяжении во всех трех измерениях. Этот факт может быть неочевидным сначала, поскольку многие артефакты скрывают свою триангуляцию внутри своей формы, например, квадратные стены и крыши зданий. С другой стороны, структуры тенсегрити показывают силы, действующие на них, путем разделения векторов растяжения и сжатия на отдельные компоненты. Большинство из них основаны на итерациях регулярных геометрических форм, известных как пять Платоновых Тел.Полная триангуляция и полная стабильность наблюдаются только в трех из них, тетраэдре, октаэдре и икосаэдре, и они являются лучшими кандидатами для моделирования анатомии. Без треугольной связи куб и додекаэдр по своей природе неустойчивы. Все пять выпуклых правильных многогранников демонстрируют конгруэнтные грани, ребра и углы, то есть все грани равносторонние, все углы одинаковы и все ребра идентичны.

Рис. 2. Платоновы тела.

Но, как указывал Фуллер, вавилоняне, египтяне и греки моделировали свою геометрию на основе ошибочного представления о том, что объекты твердые, плоскости гладкие и ограничены краями, а края пересекаются в одной точке.Физика не обнаруживает свидетельств континуума; реальность выглядит и ведет себя больше как тенсегрити — совокупность нетвердых событий, опосредованных исключительно векторами силы растяжения и сжатия. Кроме того, никакие два события не проходят через одну и ту же точку — скорее, векторы растяжения и сжатия перекручиваются друг за другом, передавая крутящий момент или вращение геометрии. Tensegrities всегда обладают вращением по часовой стрелке и против часовой стрелки сжатия и растяжения, которые аддитивно компенсируют друг друга, чтобы гарантировать стабильность.

Тенсегрити-модели Платоновых Тел могут выявить силы, действующие на их формы. Изучая геометрию тела, кажется вероятным, что соответствующие формы тенсегрити можно аналогичным образом использовать для моделирования сил, действующих на него, и для объяснения системных функций и дисфункций. Можно сказать, что из трех правильных триангулированных многогранников только октаэдр обладает симметрией по всем трем осям. Версия этого тенсегрити, называемая расширенным октаэдром, является подходящей моделью для использования там, где мы находим эти симметрии в теле.

Рис. 3. Расширенный октаэдр тенсегрити.

Другие классы тенсегритов являются хиральными, то есть они бывают в левосторонних и правосторонних версиях того, что выглядит как наклонные или повернутые призмы. Они кажутся более подходящими в качестве асимметричных моделей рук и ног.

В живой структуре стабильность сочетается с подвижностью, а объекты, которые приспособлены для движения, обладают степенями свободы и не полностью триангулированы. Степени свободы относятся к числу различных способов, которыми твердый объект может перемещаться в трех измерениях (шесть).Это: движение вверх и вниз (качание), движение влево и вправо (раскачивание), движение вперед и назад (помпаж), наклон вверх и вниз (качка), поворот влево и вправо (рыскание) и наклон из стороны в сторону (перекатывание). . Механизм или связь, соединяющая более одного объекта, может иметь больше степеней свободы, чем для одного жесткого объекта. Например, считается, что человеческая рука имеет семь степеней свободы: три в плече, одну в локте и три в запястье. Управление степенями свободы означает повышение стабильности объекта, и в любом суставе все другие нежелательные степени свободы ограничиваются комбинацией геометрии кости и соединительных элементов.

Рис. 4. Четырехкратная призма Тенсегрити.

Поскольку тенсегриты никогда не бывают полностью жесткими, они обладают различными степенями свободы, диапазон движения которых определяется их триангуляцией. В этом отношении они внешне больше похожи на растения, чем на подвижные существа. Они могут сгибаться и приспосабливаться к векторам силы, слегка изменяя форму. Они скорее гнутся, чем ломаются. Но периферия тела демонстрирует широкий диапазон движений, который варьируется в каждом суставе. Для того, чтобы tensegrities имитировали анатомию, необходимо увеличить диапазон движений без ущерба для стабильности или степеней свободы.

В медицинской терминологии диапазон движения — это измерение расстояния, достижимого между согнутым положением и разогнутым положением определенного сустава или группы мышц, обычно измеряемое в градусах. Но в определениях тенсегрити речи не идет об артикуляции. На самом деле, если вы посмотрите на напряженности Фуллера и Снельсона, они напоминают сферу, купол или мачту — никаких стыков нет. Чем они больше и чем больше они весят, тем большее напряжение добавляется к предварительному напряжению и тем меньшим диапазоном движения они обладают.Это ключ к попытке найти соответствие между анатомией и тенсегрити. Как концепция, принцип и теория связаны со сложным расположением костей неправильной формы и фасций, связок и сухожилий, которые воздействуют на суставные суставы нашего тела?

Одна попытка ответить на эту загадку моделирует реальную форму костей с их прикреплениями в виде напряжений. Существует прямая зависимость между приложенной нагрузкой и морфологией кости. Закон Вольфа о преобразовании костей гласит, что каждое изменение функции кости сопровождается определенными определенными изменениями во внутренней архитектуре и внешнем строении в соответствии с математическими законами.Это означает, что внешняя форма кости хорошо адаптирована к действующим на нее силам. Другими словами, геометрия кости демонстрирует, что форма следует за функцией. ⁵ Это можно продемонстрировать с помощью модели тенсегрити, которая отображает векторы сил, проходящих через кость. Если кость и ее прикрепления (например, бедренная кость) можно описать как тенсегрити, которая взаимодействует с другой (например, большеберцовой костью), то любой сустав можно рассматривать как интерфейс между двумя тенсегрити. Взятые вместе, они образуют артикулирующую тенсегрити, которая превосходит суммы их индивидуального поведения.Поскольку каждый компонент тенсегрита (элементы сжатия и растяжения) можно рассматривать как состоящий из меньших тенсегритов, тело рассматривается как фрактальное и иерархическое. Тело в целом всегда синергетически вовлечено в действия периферии. Точно так же сочленения последовательных суставов, таких как пальцы, запястье, локоть, плечо, делают больше, чем просто суммируются — их влияние умножается.

Геометрия корпуса

Ядро тела, туловище, вероятно, легче всего смоделировать, используя принципы тенсегрити.Он имеет двустороннюю симметрию, колеблется (дышит) и со всех сторон ограничен костными структурами. Дыхание заставляет грудную клетку расширяться и сжиматься вслед за перекачивающим действием диафрагмы. Несколько абстрагируя форму, можно сопоставить векторы сил туловища с расширенным октаэдром тенсегрити (каждая из трех осей октаэдра была удвоена и разделена, создавая пустоту внутри).

Рис. 5. Модифицированный X-Octa Tensegrity.

Это один из очень немногих тенсегритов, демонстрирующих симметрию в трех плоскостях, и он хорошо подходит для моделирования туловища.Это тенсегрити сжимается и расширяется так же, как и туловище, и в теле есть центральная полость, созданная геометрией. Когда две параллельные стойки раздвигаются (что эквивалентно, например, расширению ребер), обе другие параллельные пары также интуитивно расширяются и отталкиваются друг от друга. Когда нагрузка прилагается, как тело штангиста в момент подъема, напряжение сжимается за счет вращения вниз и уменьшается. Построенные всего из шести стоек (соответствующим образом модифицированных), они соответствуют граничным плоскостям туловища — поперечным плоскостям ключицы и таза, корональным плоскостям позвоночника и грудины и сагиттальным плоскостям ребер с обеих сторон.Помимо этих двусторонних отношений, члены сжатия также имеют восемь трехсторонних ассоциаций. Как и во всех тенсегритах, крутящие моменты, возникающие в треугольных отношениях, компенсируются. Есть восемь треугольников с натяжением турбины, четыре по часовой стрелке и четыре против часовой стрелки, которые соответствуют восьми секциям туловища. Кроме того, диапазон движения и степени свободы тенсегрити расширенного октаэдра точно соответствуют туловищу. Фактическая геометрия (и анатомия) более сложна, но узор различим.Если это достоверное сравнение, стоит изучить мускулатуру, чтобы определить спиральные вращения в этих областях и использовать поведение модели для прогнозов.

Геометрия позвоночника

Несколько лет назад я заметил сходство между отдельными грудными позвонками и звездчатыми тетраэдрами.

Рис. 6. Тенсегриты звездчатого тетраэдра.

Это заинтриговало меня, так как сложенные друг над другом звездчатые тетраэдры могут быть подвешены в системе натяжения, образуя гибкие, но стабильные мачты тенсегрити.В позвонках угол между остистым отростком и передним нижним телом позвонка образует два плеча тетраэдра; два других плеча — это поперечные отростки. Мачта тенсегрити, как и позвоночник, функционирует как в вертикальном, так и в горизонтальном положении и может принимать нагрузки в любом положении.

Рис. 7. Тенсегрити позвоночник.

Остистый отросток верхнего грудного позвонка зависит от поперечных отростков нижнего позвонка и может допускать частичное подвешивание тенсегрити.Но в шейном и поясничном позвонках геометрия отличается, и ее труднее представить. Суставные фасетки в поясничном отделе расположены под углом, чтобы выдерживать поддерживающую нагрузку, а затылочная и грудопоясничная фасции могут играть определенную роль в дополнение к связкам и мышцам. Необходим дополнительный анализ, чтобы выяснить, какую роль тенсегральная подвеска играет в поддержке позвоночника. В любом случае межпозвоночные диски, которые действуют как соединители, также можно смоделировать как подушки тенсегрити, которые могут воспринимать и передавать нагрузки.

Рис. 8. Диск Тенсегрити.

Тело позвонка также в некоторой степени сжимаемо, как жесткая пружина (и может быть смоделировано призмами тенсгрити). Tensegrities на tensegrities внутри больших tensegrities… модель, достаточно сложная, чтобы описать реальное поведение позвоночника.

Геометрия таза

Поскольку таз также демонстрирует двустороннюю симметрию, другой модифицированный расширенный октаэдр может быть добавлен к туловищу для представления подвздошной кости и обеспечения соединения бедренной кости.

Рис. 9. Тенсегрити торс и таз.

Таз представляет собой сложную конструкцию, и это решение весьма абстрактно. Он ориентирован вдоль знакомой оси «x, y и z» и схематически изображает таз, который имеет эквивалентные ориентации (слева / справа, сверху / снизу, спереди / сзади). Горизонтальные распорки (x, z) иллюстрируют динамический баланс подвздошной кости по отношению к позвоночнику и бедрам, которые представлены вертикальными (ось y) распорками.

Рис. 10. Тенсегрити таз сбалансирован.

Патомеханика таза и поясницы иллюстрируется сокращением или удлинением отдельных элементов напряжения, которые эквивалентны гипо- или гипертонусу части мускулатуры таза.Используя эту модель, можно исказить один или несколько компонентов растяжения (связок / мышц) и наблюдать за общим воздействием на структуру.

Обратите внимание, что изменение длины (или натяжения) только одного компонента растяжения (например, крестцово-подвздошной связки или тазового дна) вызывает деформации всей конструкции по всем трем осям. Эта модель показывает, что изменение длины компонента растяжения эквивалентно увеличению или уменьшению подвижности в этой области тела.

Эта модель также демонстрирует походку.Когда распорки бедра (ось z) шарнирно соединяются, имитируя ходьбу, соответствующий крутящий момент в распорках (ось x, y ’) демонстрирует вращение в подвздошной кости. Искажая один элемент натяжения, можно наблюдать соответствующее искажение походки.

Более сложный взгляд на геометрию убедительно свидетельствует о том, что таз организован в виде октетной фермы. Фермы октетов представляют собой всестороннюю триангулированную пространственную структуру, состоящую из октаэдров и тетраэдров в массиве плотной упаковки. Это чрезвычайно прочная и легкая конструкция, которая распределяет силы по шести осям, образующим ребра связанных многогранников.Он широко используется в крышах с фермой для очень больших зданий, но его механические преимущества не зависят от масштаба.

Рис. 11. Тенсегрити несбалансированный таз.

Эта модель также демонстрирует походку. Когда распорки бедра (ось z) шарнирно соединяются, имитируя ходьбу, соответствующий крутящий момент в распорках (ось x, y ’) демонстрирует вращение в подвздошной кости. Искажая один элемент натяжения, можно наблюдать соответствующее искажение походки.

Более сложный взгляд на геометрию убедительно свидетельствует о том, что таз организован в виде октетной фермы. Фермы октетов представляют собой всестороннюю триангулированную пространственную структуру, состоящую из октаэдров и тетраэдров в массиве плотной упаковки.Это чрезвычайно прочная и легкая конструкция, которая распределяет силы по шести осям, образующим ребра связанных многогранников. Он широко используется в крышах с фермой для очень больших зданий, но его механические преимущества не зависят от масштаба.

Рис 12. Октетная ферма

Каждая подвздошная кость представляет собой тетраэдр, шарнирно соединяющий лобковую кость и крестец. Лобковая ветвь и седалищный бугор образуют треугольную плоскость, которая повернута примерно на 90 градусов к плоскости подвздошной ямки и гребня.Эти плоскости образуют четкую тетраэдрическую связь. Расстояние между подвздошными костями создает восьмигранную полость, из которой крестец образует лицо. Остальная часть геометрии заполнена связками и мышцами тазового дна.

Рис. 13. Схема таза.

Это точно такое же отношение, которое имеют два тетраэдра к октаэдру в октетной ферме.

Модель тенсегрити такого расположения может продемонстрировать связанный, но гибкий диапазон движений в тазу и силы, действующие через кости, связки и мышцы.

Рис.14. Октет таза.
Рис. 15. Тенсегрити-октет таза.

Можно сказать, что геометрия описывает расположение в пространстве, а тенсегрити показывает, как оно устроено. Как и положено их сложному характеру, всегда есть несколько способов натянуть тенсегрити. Другими словами, эта модель является приблизительной и наиболее вероятной. Возможны и другие решения наблюдаемой геометрии.

Геометрия соединения

Попытка смоделировать диапазон движений и степени свободы наших конечностей — это лакмусовая бумажка гипотезы биотенсегритичности.Как уже отмечалось, традиционное определение тенсегрити не включает суставы. Кроме того, предварительное напряжение может быть настолько высоким, что трудно представить, как соединение тенсегрити может быть текучим. Кеннет Снельсон, который больше, чем теоретик, создает напряженность и понимает проблему. Он заметил мне, что «x с тенсегритизмом трудно управлять всеми линиями предварительного напряжения, чтобы управлять движением динамически так, как наши мышцы обеспечивают все телесные колебания, вращения, толчки, тяги и их вариации.«Но есть способ продолжить. Используя (тетраэдрическую) натяжную стропу, можно связать дискретные геометрические формы тенсегрити (как обсуждалось) вместе, чтобы сформировать универсальный шарнир. Тетраэдрический «седловой шарнир» имеет две степени свободы и широкий диапазон движения в двух плоскостях, разнесенных на 90 градусов.

Рис. 16. Тетраэдрический седловой шарнир.

Если ограничена одна степень свободы, полученный шарнир начинает двигаться как колено, за исключением того, что он чрезмерно расширяется как кзади, так и кпереди. Разумная настройка геометрии приводит модель в большее соответствие с движением колен.Внимательное изучение мыщелков бедренной кости и возвышения большеберцовой кости выявляет силы, действующие на них, и показывает правдоподобную седловидную взаимосвязь, которую можно смоделировать как два переплетающихся тенсегрита.

Рис. 17. Тенсегрити Колено-седло.

Два модифицированных расширенных октаэдра, повернутых на 90 градусов друг к другу в осевом направлении, демонстрируют удивительно близкое соответствие геометрии колена.

Рис. 18. Конструкция колена тенсегрити.

Кроме того, надколенник представляет собой кость четырехгранной формы, которая располагается в промежутке между бедренной и большеберцовой костью, ее положение поддерживается другой натяжной петлей седла между мыщелками бедренной кости.В рамках этой упрощенной модели малоберцовая кость считается частью тенсегрити большеберцовой кости.

Рис.19. Тенсегрити согнуты в коленях.

Но как добиться плавного, но контролируемого движения? Добавление второго уровня натяжения, пересекающего сустав или суставы, без необходимости нести всю нагрузку предварительного напряжения, позволило бы расширить диапазон движений в руке или ноге. Предварительное напряжение двух напряжений не суммируется и не пересекает соединение, поэтому оно перемещается свободно.

Предполагается, что связки и фасция действуют как более глубокие слои напряжения, которые несут предварительное напряжение, и мышцы стабилизируются (степени свободы), но также могут свободно действовать через интерфейс (диапазон движения).Опять же, необходимы дополнительные исследования.

Призмы Тенсегрити

Класс киральных (зеркальных) напряжений, известных как Т-призмы, иллюстрирует винтовые силы, которые действуют как нелинейные пружины. Их можно связать смежными слоями любой длины и любого обхвата.

Рис. 20. Спиральная мачта Тенсегрити
Рис. 21. Конструкция стопы тенсегрити.

По часовой или против часовой стрелки, однослойные, четырехкратные Т-образные призмы подходят для описания переноса веса с ноги на стопу.Таранная кость распределяет нагрузку как сзади на пяточную кость, так и спереди на ладьевидную кость и другие кости предплюсны. Геометрия Т-призм аналогична: она обеспечивает надежный амортизатор, а спиральное вращение при сжатии имитирует пронацию от шагов. Накопленная энергия затем высвобождается, когда она расширяется, обеспечивая отскок.

Они сжимаются вдоль вертикальной оси, потому что их триангуляция является гибридной и неполной (частично сжимающей и частично растягивающей), но их можно усилить путем добавления компонентов для придания любой степени жесткости.

Что дальше?

В этом беглом взгляде на применение биотенсегрити к геометрии анатомии я попытался передать некоторые внутренние механизмы тенсегрити. Мои наблюдения и идеи являются умозрительными, а мои модели приблизительными; необходимо сделать больше, чтобы заполнить детали. Поскольку расследование только начинается, мне интересно, как это будет воспринято со временем в более широком медицинском сообществе. Благодаря силе идеи, а также трудам и презентациям Фуллера, Снельсона, Ингбера, Левина и многих других, очевидно, что идеи тенсегрити повлияют на следующее поколение ученых и художников.Я намерен предоставить некоторые средства для продолжения дискуссии в продуктивном и научном направлениях. Я не претендую на то, чтобы заниматься наукой; скорее я закладываю основу для будущих научных исследований и исследований. В конечном счете, если это подходит, я ожидаю увидеть существующие и будущие методологии исцеления, включающие понимание и сильные стороны тенсегрити в свои техники и приложения.

Новые итерации биотенсегрити находятся в стадии разработки, и я приглашаю заинтересованных людей связаться со мной и поделиться своими комментариями и предложениями.Исследования включают исследования в смежных областях, таких как дизайн протезов, экзоскелеты и робототехника. Преимущества tensegrities настолько очевидны (сила, устойчивость, вес), что я ожидаю, что они сыграют ключевую роль в будущем развитии этих и других технологий.

Заключительное замечание: даже если с телами обращаются как с целым, они встроены в свою социальную и физическую матрицу и играют свою роль в клубке более крупного сообщества тенсегрити. Но это пусть Карлос Кастенада и Стаффорд Бир разберутся…

Все фотографии и иллюстрации принадлежат T.Э. Флемонс 2006

1. Сальвадори, Марио, 1980, Почему строятся здания , Нортон, стр. 83–84

2. Википедия, http://en.wikipedia.org/wiki/Tensegrity

3. Фуллер, Р. Бакминстер, 1975, Synergetics , Macmillan, стр. 372

4. Кеннет Снельсон, интервью, http://www.kennethsnelson.net/faqs/faq.htm#1

5. Неттер, Ф.Х., 1987, Том 8, Костно-мышечная система , стр. 187

Авторские права © T.E. Флемонс 2007

Работа с импортированной геометрией

Автор: Джо Медейрос, Javelin Technologies Inc.

В этой статье мы увидим, как мы можем захватить поверхности из импортированной модели и использовать их для создания справочной геометрии для компонентов пресс-формы. Многие из этих шагов также могут быть применены к кованым деталям, а также к проектированию инструмента и штампа. Некоторые шаги, описанные в этой статье, можно значительно автоматизировать с помощью инструментов SolidWorks Mold Tools, и я бы рекомендовал использовать онлайн-руководство, чтобы ознакомиться с этими инструментами. Доступ к онлайн-руководству можно получить на вкладке ресурсов панели задач SolidWorks.

Диагностика импорта

Первым шагом при работе с импортированными моделями является запуск диагностики импорта, чтобы убедиться в отсутствии дефектов поверхности с импортированной геометрией. Диагностика импорта проверяет импортированную модель на наличие дефектов и зазоров, и ее можно использовать для исправления этих дефектов. Диагностика импорта недоступна после создания элементов в SolidWorks; поэтому перед созданием каких-либо функций следует запустить диагностику импорта. Вы можете запустить диагностику импорта, щелкнув правой кнопкой мыши импортированное тело или поверхность и выбрав «Импорт диагностики» из контекстного меню .

Запуск диагностики импорта из контекстного меню

После того, как мы закончим исправление любых плохих лиц или пробелов, нам все равно нужно проделать некоторую дополнительную работу, прежде чем мы начнем моделировать. Импортированная деталь может содержать мелкие грани или другие дефекты, которые могут вызвать трудности с такими операциями, как смещение поверхности. В SolidWorks есть два инструмента, которые можно использовать для поиска проблемных областей.

Проверить сущность

Первый доступен из меню инструментов и называется Проверка .Одна из основных вещей, которые мы хотим проверить, это то, что минимальный радиус кривизны больше, чем значение любой изогнутой грани, которую мы хотим смещать. Если минимальный радиус меньше значения смещения, смещение может не сработать.

Проверка минимального радиуса кривизны

Утилита анализа геометрии

Утилита Geometry Analysis, которая является частью надстройки SolidWorks Utilities, предоставляет более подробный отчет о потенциальных проблемах с импортированной моделью.Нажав на «Рассчитать», мы сможем найти все проблемные области. Надстройка SolidWorks Utilities доступна в SolidWorks Office Professional и более поздних версиях.

Запуск утилит SolidWorks Geometry Analysis

После того, как импортированная модель исправлена и мы исправили как можно больше геометрических недостатков, мы готовы сгенерировать детали из импортированной модели. Как упоминалось ранее, во многих случаях мы можем использовать SolidWorks Mold Tools, чтобы быстро создать полость сердечника, а также любые вставки.В тех случаях, когда мы не можем использовать Solidworks Mold Tools, мы можем создать компоненты пресс-формы вручную, выполнив следующие действия.

Анализ проекта

Первым шагом в создании наших компонентов пресс-формы, независимо от того, используем ли мы инструменты Solidworks Mold или ручной подход, является выполнение анализа уклона, чтобы убедиться, что наша деталь имеет требуемый уклон. Инструмент анализа уклона раскрасит различные грани в соответствии с направлением вытягивания и определит, имеют ли грани минимально необходимый уклон.Установив флажок «Классификация лиц», мы получим возможность сохранить эти цвета при выходе из инструмента «Анализ черновика». Сохранение цвета лица может быть очень полезным при создании нашего инструментария, если нам нужно использовать ручной подход, как мы увидим позже в этой статье. Если для граней требуется уклон, можно использовать команды «Уклон» и «Разрезать линию» для добавления необходимого уклона.

PropertyManager Анализ уклона

Утилита выбора мощности

В случаях, когда мы не можем создать наши инструменты с помощью SolidWorks Mold Tools, часто может быть гораздо более эффективным создание нашего сердечника, полости, вставок и электродов в виде отдельных файлов деталей; вот где цвет лица может быть очень полезным.Надстройка Utilities содержит инструмент под названием Power Select , который можно использовать для выбора граней на основе цвета. Мы можем использовать эту утилиту, чтобы быстро выбрать грани, принадлежащие нашему ядру и полости, которые были нарисованы с помощью Draft Analysis.

Использование утилиты Power Select для выбора лиц по цвету

Сохранить как Parasolid

После того, как мы выбрали грани с помощью утилиты Power Select, мы можем сохранить эти грани как Parasolid из диалогового окна «Сохранить как».Когда мы предварительно выбрали грани, команда «Сохранить как» позволяет нам сохранить все тела, выбранные тела или выбранные грани. Мы будем использовать параметр выбранных граней, чтобы сохранить только те грани, которые нам нужны для сердечника или полости и любых вставок.

Опции экспорта «Сохранить как»

Теперь мы открываем недавно созданный Parasolid в новый файл детали. Уменьшая количество граней / поверхностей, с которыми нам приходится иметь дело, мы можем значительно повысить производительность, особенно для файлов сложных деталей или деталей, содержащих только поверхности.Когда мы откроем Parasolid, мы все равно должны запустить диагностику импорта, чтобы убедиться, что нет плохих сторон или пробелов. Поскольку мы имеем дело с меньшим количеством граней / поверхностей, ремонт модели должен быть проще и потребует меньше времени. Мы также должны проверить наличие других потенциальных проблем с помощью таких инструментов, как Проверка и Анализ геометрии.

Использование инструментов для обработки поверхностей для создания конструкций пресс-форм

Убедившись, что у нас чистая геометрия, нам нужно объединить все поверхности в одну поверхность.Для этого потребуется инструмент Knit Surfacing. Вам также может потребоваться использовать другие инструменты обработки поверхностей, такие как «Заливка», для замены отсутствующих граней, создания любых перекрывающих поверхностей или закрытия зазоров, которые не удалось устранить с помощью диагностики импорта.

Геометрия трикотажной поверхности

С единственной поверхностью теперь мы можем создавать поверхности сечения или разделения, используя соответствующие инструменты поверхности, такие как Плоские поверхности, Излучающие поверхности, Линейчатые поверхности и Лофт-поверхности.После создания поверхностей перехода или разделения мы снова связываем все поверхности в единое тело поверхности. Вы можете использовать инструменты Solidworks Mold, чтобы упростить этот процесс.

Нанесено излучение на поверхность

Последняя серия шагов заключается в создании плоскости смещения на желаемом расстоянии от тела поверхности, создании эскиза на этой плоскости для компонента пресс-формы и выдавливании эскиза до тела поверхности. В качестве альтернативы мы можем выдавить эскиз за пределы тела поверхности и использовать функции «Заменить грань» или «Вырезать поверхностью».

Создание пресс-формы путем выдавливания до геометрической формы поверхности

Дополнительная информация и рекомендуемые продукты

Создание инструментов из импортированной геометрии может быть сложной задачей, но есть несколько отличных продуктов со статусом Gold Partner, которые значительно упрощают этот процесс.

Capvidia’s FormatWorks часто исправляет ошибки импорта во время процесса импорта, тем самым уменьшая необходимость в ручном ремонте. FormatWorks также имеет расширенные инструменты для устранения проблем, не обнаруженных в процессе импорта.

R&B Mold предлагает два продукта для проектирования пресс-форм. SplitWorks добавляет мощные инструменты для классификации граней, создания сердечника, полости и вставок, а также для автоматизации проектирования электродов. MoldWorks автоматизирует процесс проектирования пресс-форм, легко создавая стандартные и нестандартные пресс-формы, быстро добавляя коммерческие или некоммерческие компоненты, такие как выталкивающие штифты, винты, дюбели, уплотнительные кольца, направляющие и подъемники, а также автоматизируя создание чертежей.

Свяжитесь с нами, если вы хотите получить дополнительную информацию о наших продуктах для перевода данных или проектирования пресс-форм.

Ссылки по теме

Посмотрите видео с электронным обучением о том, как использовать SolidWorks Import Diagnostics Gap Closer
Посмотрите видео с электронным обучением о том, как восстановить импортированную модель с помощью заливки поверхности

Изгоняя блюз плохой геометрии с помощью Design Modeler — PADT, Inc. — Блог

(ПРИМЕЧАНИЕ: эта статья является перепечаткой окончательной версии PDF-файла The Focus, выпуск 74.Мы использовали его для подтверждения нового формата блога.)

Мы все были там раньше. Вы стоите перед своим компьютером, вы просто читаете свою геометрию и набрасываете быструю сетку, чтобы увидеть, что у вас есть и сколько усилий для этого потребуется. Следующее, что вы знаете, вы получаете ошибки или красные линии появляются на вашей геометрии. У вас плохая геометрия, и теперь вам нужно ее очистить.

Доступно множество вариантов, в том числе: 1) возврат к исходному САПР и исправление этого, 2) использование инструмента для ремонта, такого как CADFix, 3) использование некоторого инструмента промежуточной геометрии, который хорошо подходит для ремонта, например SpaceClaim или IronCAE, или 4 ) сетка в ICEM CFD, что гораздо проще при плохой геометрии.Все это работает, и, возможно, именно так вы справлялись с этой ситуацией в прошлом. Но вы также должны знать, что в ANSYS DesignModeler есть набор инструментов, специально созданных, чтобы помочь вам решить эту проблему.

Первое, что нужно попробовать, — это варианты, когда вы считываете свою геометрию в DesignModeler. На рисунке 1 показан соответствующий вид подробностей.

Рисунок 1: Параметры импорта

Программа может упростить геометрию, упростить топологию, лечить тело или очищать тело.Он также может попытаться заменить любую недостающую геометрию. Кстати, доступные параметры меняются в зависимости от того, откуда взялась ваша геометрия, поэтому, если вы не видите их все, это нормально. Геометрия исцеления включена по умолчанию, как и чистая. Иногда вы можете не захотеть их надевать. Поиграйте и с упрощением. Иногда изменение этих параметров может очистить все.

Если автоматические функции не работают, пора взглянуть на инструменты, доступные вам в DM. Первое, на что следует обратить внимание, — это «Поиск малых объектов». Как следует из названия, он выходит и определяет, где у вас есть небольшие объекты, и дает вам их размер.Вы получаете доступ к команде немного иначе, потому что это не то, что вы вставляете в дерево. Перейдите в Инструменты> Инструменты анализа> Поиск по малым объектам. Появится подробное представление, показанное на рисунке 2.

Рисунок 2: Малые предприятия

Выберите одно или несколько тел, которые вы хотите проверить, и установите параметры, хотя значения по умолчанию обычно хороши. Тогда это странная часть, измените параметр рядом с «Вперед!» на «Да». Он выполнит поиск и представит результаты ниже.Щелкните любой элемент в списке, и вы сможете увидеть его на экране. Это должно помочь вам понять, где у вас могут возникнуть проблемы, прежде чем вы начнете что-то исправлять.

Наш любимый инструмент восстановления в DM — это инструмент Merge. Он берет края или поверхности, которые соединяются без острых углов, и объединяет их в новые гладкие объекты. На рисунке 3 показан типичный пример для кромок, а на рисунке 4 — для поверхностей.

Рисунок 3: Объединить края

Рисунок 4: Объединить грани

Вы можете выполнить автоматическое объединение или выбрать объекты, которые хотите объединить.Автоматический автомат — отличный способ избавиться от мелких осколков, не ища их. Этот инструмент также полезен для упрощения вашей геометрии, чтобы получить лучшую сетку. На рис. 5 показано, как действительно можно очистить галтели и всасывающую сторону лопатки турбины.

Рисунок 5: Слияние граней Ceanup

Иногда вы просто хотите отключить модель, удалив отверстия, скругления, выступы и т. Д. Вы можете сделать большую часть этого с помощью команд «Удалить кромку» и «Грань».Их можно найти в разделе Инструменты, и они работают так, как вы ожидаете. Вы просто определяете грань или край, который хотите удалить, а программа удаляет их и лечит твердое тело. На рисунках с 6 по 8 показаны примеры. Мы пришли к выводу, что это наиболее эффективный и контролируемый способ искажения модели и избавления от крошечной геометрии, которая вызывает проблемы.

Рисунок 6: Удаление граней для удаления скруглений

Рисунок 7: Удаление кромок

Рисунок 8: Удаление граней для удаления элементов

Если после использования упомянутых выше инструментов у вас все еще есть плохая геометрия, вы можете разобраться и испачкаться с помощью набора инструментов для ремонта, которые решают наиболее распространенные проблемы.Все они находятся в разделе Инструменты-> Ремонт. Имена говорят сами за себя. Существуют инструменты для удаления щепок, шипов, мелких краев, мелких поверхностей, швов, отверстий и остроугольных поверхностей. Большинство из них работают одинаково — вы можете указать размер, и любые элементы ниже этого размера будут очищены, или вы можете выбрать геометрию. На остальных рисунках показаны примеры различных вариантов.

Рисунок 9: Инструменты для ремонта

Небольшое примечание, прежде чем мы закончим, большинство параметров, доступных в меню, могут отображаться в виде значков на панелях инструментов, если вы перейдете в Инструменты-> Параметры-> Панели инструментов.Если вы делаете много ремонтных работ, мы рекомендуем вам добавить инструменты, которые вы используете, на панели инструментов. Еще одна важная вещь, которую должны знать пользователи, — это то, что вы можете восстановить геометрию и сохранить ее как файл ANSYS ANF, собственный формат файла для ANSYS Mechanical APDL. Таким образом, даже если вы не создаете сетки и не выполняете предварительную обработку в Workbench, вы все равно можете использовать этот инструмент для очистки своей геометрии.
Потратив годы на исправление плохой геометрии, мы очень рады включить эти инструменты в наш основной программный продукт, избавляя от необходимости переходить к другим программам.Потратив время на изучение этих инструментов, когда они работают, а когда нет, и понимание их возможностей окупились, избавившись от нашей плохой геометрии.

Нравится:

Нравится Загрузка …

Связанные

Кинематическая геометрия масс-треугольников и приведение уравнения Шредингера систем трех тел к уравнениям в частных производных, определяемым исключительно на треугольных параметрах

Abstract

Уравнение Шредингера системы трех тел — это линейное уравнение в частных производных (PDE), определенное в 9-мерном конфигурационном пространстве ℝ ⁹, естественно снабженное кинематической метрикой Якоби, а также трансляционной и вращательной симметрией.Естественная инвариантность уравнения Шредингера относительно трансляционной симметрии позволяет нам уменьшить конфигурационное пространство до 6-мерного, в то время как вращательная симметрия обеспечивает квантово-механическую версию сохранения углового момента. Однако проблема максимального использования вращательной инвариантности, чтобы позволить нам свести уравнение Шредингера к соответствующим УЧП, определенным исключительно на треугольных параметрах, т. Е. На уровне ℝ ⁶/ SO (3), никогда не решалась. адекватно лечился.В этой статье описываются результаты по геометрии орбиты и гармонический анализ ( SO (3), ⁶), которые позволяют нам получить такую редукцию уравнения Шредингера для трехчастичных систем к УЧП, определенным исключительно на треугольных параметрах. .

В атомной и молекулярной физике естественным образом встречается квантовая механика трехчастичных систем, таких как атом гелия He, молекулярный ион водорода H ₂ ⁺, отрицательный ион атома водорода H ^— и т. Д.Основным уравнением для изучения физики таких систем является уравнение Шредингера , а именно 1, где U — потенциальная функция, E — уровень энергии стационарного состояния и μ _j и Δ _j являются, соответственно, индивидуальной массой и оператором Лапласа относительно координат отдельной частицы, j = 1, 2, 3.

Исследование приведенного выше уравнения трех тел Шредингера systems имеет долгую историю, восходящую к работе Хиллерааса по этому вопросу в 1930-х годах, и существует обширная литература и различные подходы к изучению ее решений.Книга Бете и Солпитера (1) и том Festschrift Review of Modern Physics в честь Хиллерааса (2) содержат много основных ссылок по этой теме.

Проблема максимизации использования сохранения углового момента, однако, никогда не рассматривалась должным образом. Обычная процедура состоит в том, чтобы ввести приближения, такие как приблизительные приведенные массы и т. Д. В этой короткой статье я опишу геометрический подход к задаче трех тел, который не использует , а не каких-либо приближений или возмущений и, следовательно, применим к общим массовые распределения как однобокие.Следуя Якоби, естественно ввести риманову метрику в конфигурационном пространстве данной механической системы так, чтобы кинетическая энергия движения была равна половине квадрата скорости. Такое кинематическое риманово многообразие на самом деле является геометрической кодировкой кинетической энергии данной системы и всегда наследует изометрию SO (3) — от вращательной симметрии физического пространства. Кроме того, пространство SO (3) -орбит также имеет индуцированную метрику , которая измеряет расстояния между соседними орбитами.Таким образом, мы называем это метрикой орбитального расстояния . В частном случае систем из трех тел пространство орбит, M ̄ , является в точности «пространством треугольников» (т. Е. Каждая точка из M ̄ представляет собой класс конгруэнтных треугольников) и вышеупомянутой метрикой орбитального расстояния ds̄ ², обеспечивает естественное геометрическое измерение разницы в размере и форме между треугольниками. Пусть I будет моментом инерции . Тогда ρ = равно расстоянию между заданным треугольником и точечным треугольником, таким образом, ρ обеспечивает естественное измерение размера, в то время как 2-мерное подпространство M * ⊂ M̄ , определенное путем установки ρ = 1, является естественное геометрическое представление всех возможных форм треугольников.Замечательная внутренняя красота кинематической геометрии треугольников заключается в том, что M * всегда изометрично евклидовой полусфере радиуса ½, S ₊ ² (½), (т. Е. Независимо от массы распределение).

Уравнение Шредингера естественно SO (3) — инвариант , и это является источником сохранения углового момента в квантовой механике. Вышеупомянутая установка SO (3) -орбитальной геометрии конфигурационного пространства позволяет нам максимально использовать сохранение углового момента [или, скорее, SO (3) — инвариантность трехчастичной системы] свести уравнение Шредингера к системе l + 1 (соответственно l ) УЧП на уровне ( M̄ , ds̄ ²), а именно, исключительно в терминах треугольных параметров , cf .Уравнения. 20 и 20 * .

Комбинация сферичности M * и приведенных выше сокращенных уравнений позволит нам еще больше сократить решение уравнения. 1 к бесконечной системе алгебраических линейных уравнений (3, 4).

Кинематическая геометрия треугольников и конкретный выбор координат конфигурационного пространства

Пусть μ = ∑ μ _j — полная масса, м _j = μ _j / μ — процентные доли массы, j = 1, 2, 3 и a _j — векторы положения.Следуя Якоби, кинематическая метрика на ℝ ³ ⊕ ℝ ³ ⊕ ℝ ³ определяется установкой 2 Более того, фиксация начала координат в центре тяжести позволяет нам уменьшить пространство конфигурации до 6 -мерное линейное подпространство ℝ ⁶, заданное как ∑ m _j a _j = 0. Операторы Лапласа на обоих ℝ ⁹ и выше ℝ ⁶ задаются 3 Таким образом, уравнение Шредингера ( 1 ) может быть переписано как 1` Важная отправная точка для достижения « SO (3) -редукции» уравнения.1 ′ — это следующий конкретный внутренний выбор системы координат в ℝ ⁶, а именно установка 4 Then 5 Таким образом ℝ ⁶ ≅ {( x , y ) = (ξ ₁, ξ ₂, ξ ₃, η ₁, η ₂, η ₃), ξ _j, η _j ∈ ℝ} обеспечивает хорошую декартову систему координат ( SO 902 (3), ℝ ⁶), что является преимуществом для SO (3) -гармонического анализа в его функциональном пространстве.Набор 6 Хорошо известно, что каждый SO (3) -инвариантный полином от {ξ _j, η _j} может быть однозначно выражен как полином от { f ₁, f ₂, f ₃}. Таким образом, ( f ₁, f ₂, f ₃) также составляет естественную систему координат пространства орбиты M ̄ . Установите 7 и пусть ( g _ij) будет обратной матрицей ( g ^ij).Тогда метрика орбитального расстояния, ds̄ ², на M̄ дается 8 Леммой 1. Пусть Ψ = Ψ ( f ₁, f ₂, f ₃) — инвариантная функция SO (3) — , а Δ, Δ̄ — оператор Лапласа на (ℝ ⁶, ds ²), ( M̄ , ds̄ ²) соответственно. Тогда 9 , где v = [det ( g ^ij)] ^1/2 — постоянный множитель функции объема SO (3) — орбиты .

Теорема (ссылка 5). Набор 10 Тогда 11 Кроме того, подмножество θ = π / 2 представляет вырожденные m-треугольники и содержит три конкретные точки с φ = φ _i, i = 1, 2 , 3, , представляющие три формы бинарных столкновений, где 12 Кроме того, расстояние r _ij, между i-й и j-й частицами задается формулой 13 Замечания .На M̄ есть три набора основных координат (т. Е. Треугольных параметров), а именно: { I _j} является естественным для кинематики , { f _j} равно естественное для алгебры [такое как SO (3) -представление], в то время как (ρ, θ, φ) является геометрически оптимальным, который раскрывает сферичность ( M̄ , ds̄ ²). Следовательно, координаты (ξ _j, η _j) на ℝ ⁶ и ( f _j) на M̄ , которые используются в следующем разделе, являются предпочтительными. для получения приведения уравнения Шредингера с уровня ℝ ⁶ до уровня M ̄ = ℝ ⁶/ SO (3).Однако после того, как такое уменьшение уже достигнуто, естественно перейти к сферическим координатам (ρ, θ, φ). Например, Лемма 1 может быть переписана следующим образом.

Лемма 1 ′. Пусть f = F (ρ, θ, φ) — инвариантная функция SO (3) — от ℝ ⁶. Тогда 9`

Приведение уравнения Шредингера (1 ‘) к УЧП исключительно в терминах треугольных параметров

Уменьшение уравнения Шредингера ( 1 ′ ) с уровня ℝ ⁶ до уровня M̄ можно рассматривать как улучшение и уточнение обычной версии «сохранения углового момента» в квантовой механике.В терминах вышеуказанных координат оператор углового момента является следующим векторным оператором, а именно 14. Более того, 15 являются некоторыми из связанных с ним операторов, часто полезных при изучении углового момента в квантовой механике. Установить 16 Тогда легко проверить, что 17 и оба h _{α, β} и h * _{α, β} являются общими нулями для Δ _ξ, Δ _η и Δ _ξη. Следовательно, из Ур. 16 и 17, что все h _{α, β} ^{( k )} и h _{α, β} ^{∗ ( k )} — это общих нулей Δ _ξ, Δ _η и Δ _ξη.

Теорема 1 (ссылка 6). Пусть ℂ [ξ, η] — кольцо комплексных полиномов коэффициентов в {ξ _j} и {η _j} и ℛ — подкольцо SO (3) — инвариантных единиц (т.е. полиномы от { f _j}). Тогда ℂ [ξ, η] является «векторным пространством» над ℛ с { h _{α, β} ^{( k )}; h _{α, β} ^{∗ ( k )}} в качестве особой основы, что означает, что каждый элемент ℂ [ξ, η] может быть однозначно выражен как линейная комбинация { h _{α, β} ^{( к )}; h _{α, β} ^{∗ ( k )}} с коэффициентами в ℛ.

Примечания . Указанное выше конкретное семейство базисных функций с точностью до постоянных множителей характеризуется следующими свойствами:

( i ) бигармоничность — т.е. общие нули Δ _ξ, Δ _η и Δ _ξη,

( ii ) биоднородность в {ξ _j} и {η _j},

( iii ) общих собственных функций для J ² и J ₃, а именно 18 Теорема 2 (см.6). Для каждой данной пары азимутальных и магнитных квантовых чисел (ℓ, м ), | м | ≤ ℓ> 0, существуют два отдельных квантовых типа, волновые функции которых соответственно задаются формулами 19 , где k = ℓ — m и {ψ _j} ( соответственно {ψ _j ^∗}) составляют (ℓ + 1) — кортеж ( или ℓ- кортеж ) из SO (3) — инвариантных функций, удовлетворяющих следующим системам PDE, соответственно, 20 20 * , где Δψ _j и Δψ _j ^∗ задаются формулой 9 ).

Примечания . К. Н. Ян указал на следующую корреляцию между указанным выше разделением на два квантовых типа и разделением по четности . Поскольку инвариантные функции всегда являются четными функциями, тогда как h _{α, β} ^{( k )} и h _{α, β} ^{∗ ( k )} четные или нечетные согласно (α + β) четные или нечетные, два типа волновых функций Ψ и Ψ * уравнения. 19 всегда имеют разную четность.

Доказательства приведенных выше результатов, а также следующий этап сведения к системе алгебраических линейных уравнений будут иметь место в следующих статьях, а именно в ссылках. 3–6.

СОКРАЩЕНИЕ

PDE,: уравнение в частных производных

Получено 15 октября 1996 г.
Принято 22 мая 1997 г.

Ваше руководство по построению сетки Методы эффективного моделирования CFD

Мы уже обсудили факторы, которые создают высококачественную сетку, и как подготовить геометрию модели CFD для построения сетки.В этом последующем сообщении блога вы узнаете о построении сетки под управлением физики, адаптивном уточнении сетки и о том, как использовать различные инструменты построения сетки в программном обеспечении COMSOL Multiphysics® для моделирования потоков жидкости.

Последовательности построения сетки с физическим управлением

После настройки условий потока для модели потока жидкости COMSOL Multiphysics позволяет нам вызывать последовательности построения сетки, контролируемые физикой. Такая последовательность зависит от следующих аспектов:

Настройки физических свойств
Модель турбулентности с автоматической обработкой стенок, например, дает более мелкую сетку, чем модель ламинарного потока
Некоторые особенности
Стены, например, могут создавать более мелкие сетки и сетки пограничного слоя
Размер ограничивающей рамки геометрии
Управляет масштабом размеров элементов

Управляемая физикой последовательность построения сетки для модели тела Ахмеда, которую мы также использовали в предыдущем сообщении в блоге, выглядит следующим образом:

Под узлом Mesh 1 :

Подузел Размер содержит набор параметров размера сетки, которые зависят от настроек свойств и ограничивающей рамки геометрии
Размер 1 подузел активен на всех противоскользящих стенах и требует там более мелкую сетку
Corner Refinement 1 Подузел автоматически определяет все достаточно острые углы внутри противоскользящих стен и предписывает еще более мелкую сетку вдоль этих краев (в этом случае он находит большинство острых краев на автомобиле, за исключением соединяющего крыша и скат)
Свободный тетраэдрический 1 подузел создает фактическую сетку на обеих границах и в доменах
Граничные слои 1 Подузел добавляет сетку пограничного слоя ко всем границам без проскальзывания

Увеличенное изображение сетки, полученной в результате вызванной физикой последовательности создания сетки для модели тела Ахмеда.Мы видим, что сетка на стенах более мелкая, чем в объеме, и даже более мелкая вблизи острых краев. Также видна сетка пограничного слоя на противоскользящих стенах.

Сетка, индуцированная физикой, иногда может быть достаточной для простых моделей и всегда является хорошей отправной точкой для более продвинутой сетки. С помощью сетки, показанной выше, вполне возможно решить проблему тела Ахмеда. Однако мы можем видеть, что управляемая сеткой область позади автомобиля не привела к более тонкой сетке, а неструктурированная сетка покрывает всю аэродинамическую трубу.Таким образом, сетка может быть более тонкой за автомобилем, и она излишне тонкая далеко за автомобилем. Используя домен, управляемый сеткой, за автомобилем и поверхность перегородки, показанную в первой части этой серии блогов, общее количество элементов можно приблизительно поддерживать постоянным, но с гораздо лучшим разрешением в следе.

Инструменты построения сетки для моделирования CFD в COMSOL Multiphysics®

COMSOL Multiphysics предоставляет широкий набор инструментов для управления и создания сеток. Мы можем начать с обсуждения вариантов построения сетки поверхностей, так как мы рекомендуем сначала создать сетку на гранях, чтобы убедиться в адекватном разрешении и высоком качестве элементов.Обратите внимание, что инструмент, который создает сетку для объектов определенного размера, также создает сетку для смежных объектов более низких размеров. Например, элемент Free Triangular создает сетку как для назначенных ему граней, так и для всех смежных кромок и точек, для которых ранее не было сетки. Следовательно, нам не нужно создавать сетку для всех ребер перед созданием сетки для грани, и объемы могут быть построены без предварительной сетки всех охватывающих граней.

Сопоставленная сетка

Mapping может создавать самые лучшие поверхностные сетки.На рисунке ниже показана высококачественная сетка поверхности для одной из панелей в модели солнечной панели. Отображенная сетка уточняется так, чтобы мы получали более мелкие элементы, близкие к свободным краям, и плавные переходы к мелким сеткам, покрывающим балки. Анизотропия достигается с помощью узлов Распределение , которые содержат настройки для управления количеством элементов и их распределением по краям. Тот факт, что все элементы имеют углы 90 °, означает, что элементы вообще не имеют перекоса.

Отображенная сетка на одной поверхности модели солнечной панели.

Отображенные сетки могут быть особенно полезными для 2D-моделирования, например, эталонный тест аэродинамического профиля NACA 0012, показанный ниже. Наиболее привлекательным свойством сопоставленной сетки для этой модели является чрезвычайно хороший контроль, который она обеспечивает над размером элемента, качеством и скоростью роста — даже несмотря на то, что может потребоваться некоторая работа для определения оптимального распределения по всем краям.

Отображенная 2D-сетка для модели крыла NACA 0012.

Неструктурированная четырехслойная сетка

Некоторые поверхности слишком сложно разделить на грани, которые можно нанести на карту. В этих случаях можно использовать узел Free Quad . В приведенном ниже примере показано, где грань кадра пересекается неструктурированной четырехугольной сеткой. Максимальный размер элемента на грани контролируется атрибутом Size , а атрибуты Distribution управляют распределением по ряду краев.

Неструктурированная четырехугольная сетка на поверхности модели солнечной панели.

Эту грань можно было бы объединить с помощью операции «Свободный треугольник», но в результате получится намного больше элементов. Мы также можем заметить, что скорость роста, измеренная по соседним картированным сеткам, не самая лучшая. Рама находится на нижней стороне солнечной панели, поэтому с потоком почти ничего не происходит, поэтому сетка в основном влияет на структурную механику модели, для которой скорость роста не является проблемой.

Треугольная сетка

Операция «Свободный треугольник» является «рабочей лошадкой» для 2D-моделей CFD, поскольку это быстрый и простой способ получения сеток высокого качества элементов, покрывающих всю геометрию.За простоту создания неструктурированных сеток приходится платить. Неструктурированные треугольные сетки дают большее численное распространение, чем структурированные. Это означает, что решения, полученные на неструктурированных сетках, более размыты, чем решения, полученные с использованием структурированных сеток с сопоставимыми размерами элементов. Более того, неструктурированные сетки не могут быть сильно анизотропными без перекоса.

В общем, неструктурированные сетки должны быть намного более мелкими, чем структурированные, чтобы обеспечить такой же уровень точности для задач CFD.Однако иногда может потребоваться дополнительная диффузия, поскольку становится легче добиться сходимости. Это идеально подходит для такой модели, как сверхзвуковой эжектор, показанный ниже, где сетка служит начальной сеткой для адаптации сетки (см. Ниже).

Треугольная сетка для двухмерной осесимметричной модели сверхзвукового эжектора.

Операция «Свободный треугольник» мало используется в 3D-моделях. Основное использование — «проверка сетки» отдельных граней; в частности, лица, на которых мы применили виртуальные операции.Мы можем исследовать качество сетки на отдельных гранях, не создавая сетку смежного объема. Неструктурированная треугольная сетка также может быть полезна в качестве отправной точки для сеток по траектории. Результатом такой стратегии является сетка, состоящая из призматических элементов, квадратичные стороны которых можно растягивать, тем самым создавая анизотропную сетку.

Тетраэдральная сетка

Практически все геометрические формы промышленных приложений содержат один или несколько доменов, которые просто непрактично подметать. Затем эти области должны быть покрыты тетраэдрической сеткой.Операция «Свободный тетраэдр» строит поверхностные сетки на несвязанных гранях перед построением объемных сеток. Поверхностная сетка должна соответствовать геометрическим границам, но узлы Surface Mesh могут перемещаться внутри граней во время оптимизации качества элементов. Однако грани, на которые уже нанесена сетка, остаются замороженными, что может привести к снижению качества элементов.

Тетраэдр имеет только треугольные стороны, поэтому что-то необходимо для перехода от граней с четырехугольными элементами.Это «нечто» и есть пирамида. Элемент пирамиды формально представляет собой шестигранный элемент, в котором одна из граней элемента свернута в точку, в результате чего остается элемент с одной четырехугольной гранью и четырьмя треугольными гранями. Модель солнечной панели имеет множество граней с четырехугольными элементами и, следовательно, требует, чтобы пирамиды переходили в неструктурированную сетку в области, окружающей солнечную панель, как показано ниже.

Иногда мы слышим, что пирамиды уступают другим типам элементов, но ничто не делает пирамиды плохими как таковые .Однако, когда пирамида помещается на анизотропный четырехугольник, ее основание должно иметь такую же анизотропию. Любое небольшое нарушение формы пирамиды приведет к получению элемента с довольно большим перекосом. Это показано ниже, где пирамиды, расположенные поверх сильно анизотропных четырехугольных граней на краях панелей, обычно имеют более низкое качество, чем пирамиды в центре панелей. В этом случае более низкое качество — это цена, которую мы с радостью платим за гораздо меньший общий размер сетки по сравнению с использованием неструктурированных сеток внутри панелей.

Пирамиды, расположенные поверх четырехугольных элементов геометрии солнечной панели. Элементы окрашены по качеству, рассчитанному по асимметрии.

Управление сетками, созданными с помощью операции «Свободный тетраэдр», можно значительно улучшить, используя домены управления сеткой. В примере, показанном ниже, атрибут Size 3 предписывает небольшой максимальный размер элемента на наклоне и на задней части тела Ахмеда. Атрибут размера 1 для свободного тетраэдра 1 предписывает низкую скорость роста в области управления сеткой, что приводит к мелкой сетке с низкой скоростью роста и высоким качеством элементов в области следа.Когда окружающая воздушная область является сеткой, границы, содержащие область управления сеткой, удаляются, оставляя свободу для добавления сетки пограничного слоя и перемещения элементов соседства.

Область управления сеткой за телом Ахмеда.

Мы могли бы рассмотреть скользящую сетку для области управления сеткой, описанной выше. Это сделало бы переход к остальной неструктурированной сетке более трудным и не улучшило бы ситуацию, поскольку закрученные движения, которые мы ожидаем позади «машины», относительно изотропны, а это означает, что структурированная сетка также должна быть более или менее изотропный.

Сетка по траектории

Трехмерное соответствие отображаемой сетке обозначается в COMSOL Multiphysics скользящей сеткой. Подметание берет набор исходных граней; создает сетки и проецирует их на несколько конечных граней; и соединяет эти грани с помощью призматических элементов или шестигранных элементов, в зависимости от того, имеют ли исходные сетки треугольные или четырехугольные элементы. Сдвиг идеально подходит для получения сеток, которые растянуты в направлении линии тока, сохраняя при этом заданное разрешение в плоскости поперечного сечения.

Пример показан ниже, где скользящая сетка добавлена в нижней части аэродинамической трубы модели тела Ахмеда. Внимательный человек может указать, что скорость роста между неструктурированной тетраэдрической сеткой и развернутой сеткой вблизи потолка может быть лучше. Но поле течения там почти не изменится, поэтому важнее получить хорошую скорость роста в кильватере за «машиной».

Проточная сетка после тела Ахмеда.

В приведенной выше сетке по траектории используется сетка граней из операции «Свободный тетраэдр» и операции «Граничный слой» в качестве исходной сетки. Часто это полезная стратегия. Мы могли бы создать неструктурированную треугольную сетку на границе выхода и протянуть сетку от выхода до изогнутой грани. Однако это наложило бы ограничение на операцию свободного тетраэдра (см. Раздел «Треугольная сетка»). Нам также нужно будет протолкнуть элементы пограничного слоя по всему дну аэродинамической трубы, по сравнению с созданием сетки пограничного слоя только в части с неструктурированной сеткой, а затем развернуть результат вниз по потоку.

Сетка пограничного слоя

Создание сетки граничного слоя, являющееся основным для моделирования CFD, создает сильно анизотропные сетки вблизи стен без необходимости использования развернутых сеток или специально обозначенных областей. Эти элементы необходимы из-за пограничных слоев, которые обычно образуются на противоскользящих стенах, как описано в этой предыдущей записи блога.

Сетка пограничного слоя для модели тела Ахмеда. Элементы окрашены по качеству на основе асимметрии.

В COMSOL Multiphysics сетки пограничного слоя добавляются после создания сетки домена.Анизотропные призматические или гексаэдрические элементы помещаются в расчетную область, что приводит к появлению ряда сильно анизотропных элементов, как показано ниже. Обратите внимание, качество элементов хорошее, несмотря на анизотропию. Причина в том, что сетка пограничного слоя в этом случае построена из треугольников с высоким качеством, что также приводит к высококачественным призматическим элементам.

Характеристики сетки пограничного слоя

Сетка пограничного слоя имеет три характеристики:

Высота первого слоя
Скорость роста
Количество слоев

Первый — это высота первого элемента, и она часто указывается как часть шкалы длины лицевого элемента.Типичное значение по умолчанию — масштаб длины элементов лица в 50 раз больше, чем высота первого элемента пограничного слоя. Более высокие соотношения сторон могут дать лучшее разрешение, но результирующую систему уравнений также может быть труднее решить, особенно при использовании итерационных решателей.

Вторая характеристика — коэффициент растяжения; то есть скорость роста от одного слоя элемента к другому. Это необходимо для получения приличного перехода к неструктурированной сетке (как показано выше).Отчетливо виден скачок размера элемента при переходе пограничного слоя крыши в неструктурированную сетку. Пограничный слой может иметь либо более высокий коэффициент растяжения, либо большее количество слоев в сетке пограничного слоя (количество слоев является третьей характеристикой сетки пограничного слоя). Но показанная выше сетка пограничного слоя не может быть намного толще, потому что сетка в зазоре между автомобилем и полом уже достаточно сплющена, чтобы избежать сильного перекоса в неструктурированной сетке.Это сжатие сетки пограничного слоя выполняется автоматически нижележащим алгоритмом.

Выбор высоты первого элемента, скорости роста и количества элементов — это баланс между необходимым разрешением, хорошим переходом к неструктурированной сетке и качеством результирующих элементов.

Особенности работы с острыми краями

Если вы сами упаковывали подарки, вы знаете, насколько легко бумага может порваться, если затянуть ее вокруг острых краев. Сетки пограничного слоя имеют аналогичные проблемы, как показано ниже.Элементы сетки пограничного слоя на задней острой кромке довольно перекошены, как и элементы сразу после аэродинамического профиля.

Острая задняя кромка аэродинамического профиля без специальной обработки сетки.

Один из вариантов — «разделить» пограничный слой по острым краям. Результат показан на среднем изображении ниже. Сетка пограничного слоя теперь заканчивается двумя специальными столбцами элементов, оба из которых начинаются с треугольника, за которым следует соответствующее количество четырехугольных элементов.Разделение позволяет вам контролировать, насколько острым должен быть угол, чтобы он считался острым, а также максимальный угол, который должен покрывать каждый «особый» столбец элементов. Оптимизация этих параметров может значительно улучшить качество элементов с острыми краями.

Расщепление пограничного слоя по острым краям профиля.

Разделение не всегда работает. Сложная геометрия 3D CAD, где любое количество кромок может соединяться с острым углом, особенно трудна.Алгоритм должен быть запрограммирован для каждой топологически уникальной конфигурации, и вполне вероятно, что расширенная геометрия содержит по крайней мере один острый угол, с которым алгоритм не знает, что делать.

Третий способ обработки острых углов может быть вариантом. Он называется обрезка и является параметром по умолчанию для острых углов в COMSOL Multiphysics. Результат для профиля показан ниже. По мере приближения слоя к острому краю он уменьшается по высоте на два элемента для каждого элемента, который приближается к краю.В качестве альтернативы метод можно рассматривать как наращивание количества элементов пограничного слоя от острой кромки. Количество элементов для роста и минимальный угол обрезки можно контролировать, чтобы получить оптимальную сетку.

Обрезка снижает эффективное разрешение в остром углу по сравнению с отсутствием обработки или разделения. Поэтому обрезку всегда следует сочетать с общим уточнением сетки, поэтому описанная выше функция Corner Refinement включена по умолчанию в последовательность сетки, вызванную физикой.

Обрезка — параметр по умолчанию для создания сетки пограничного слоя с острыми углами.

Сетки пограничного слоя могут повысить разрешение в узких областях. Если вы внимательно посмотрите на сетку на рисунке выше, область между автомобилем и полом покрыта 15 элементами (6 + 3 + 6). Этого достаточно, чтобы представить любой профиль скорости, который может возникнуть в этой узкой области. Без сетки пограничного слоя зазор был бы закрыт только тремя элементами, что сильно ограничивало бы способность сетки отображать профиль потока под телом Ахмеда.Затем поток обычно искусственно дросселируется, так что узкая область кажется даже более узкой численно, чем геометрически. Следовательно, сетки пограничного слоя могут быть полезны не только для турбулентных пограничных слоев, но также в ламинарных и даже микрожидкостных системах. Хорошее эмпирическое правило: узкие области должны быть разрешены как минимум с пятью элементами в поперечнике.

Копирование сеток

Наконец, мы рассмотрим, как копировать сетку из одного объекта в другой. Это возможно для объектов одного размера, если исходная сетка может быть отображена на целевом объекте с помощью перемещения, поворота и изотропного масштабирования.Это означает, что место назначения должно иметь ту же форму, что и источник, но оно может быть расположено в другом месте, каким-то образом повернуто и, возможно, иметь другой размер.

Копирование сетки особенно полезно для сопоставленных и развернутых сеток. Копирование позволяет нам заменить несколько операций сопоставления и развертки и несколько атрибутов распределения одной операцией копирования. Это возможно, если геометрия была правильно разбита, как описано в предыдущем сообщении блога. В дополнение к сохранению работы при создании сетки, любое последующее изменение сетки намного проще администрировать, так как вам нужно только изменить последовательность для исходного домена.Операция копирования автоматически переносит эти изменения в целевые домены.

Сетка с разверткой из желтого домена копируется в два розовых домена.

Адаптивная сетка

При моделировании задач CFD мы стремимся создавать плотные сетки в областях с большими градиентами. Однако бывают случаи, когда трудно предсказать, где появятся резкие градиенты. Есть также зависящие от времени случаи, когда резкие градиенты перемещаются. Это можно решить, создав мелкую сетку во всех областях, где появляются резкие градиенты, но обычно это дорого.Решение состоит в том, чтобы вместо этого вызвать адаптивную сетку.

Адаптация для стационарных задач

Одним из примеров адаптивного зацепления являются контуры давления для ударной системы, создаваемой трансзвуковым потоком через установленный на стене выступ. Удары могут быть зафиксированы схемой стабилизации, но из-за грубых сеток они будут казаться размытыми.

Контуры давления для потока Эйлера над настенным выступом.

Резкие толчки на рисунке выше получены при использовании однородной, относительно крупной сетки (показано ниже и слева).Решение на грубой сетке используется для аппроксимации остатка уравнения и уточнения сетки, где невязка велика. Уравнения решаются на получившейся более мелкой сетке. Эту процедуру можно повторять до получения удовлетворительной точности.

Сетка, используемая для вычисления поля давления выше, показана ниже и справа. Это результат того, что очень простая начальная сетка дважды адаптивно уточнялась. Адаптация по-прежнему требует работы, чтобы создать начальную сетку, поскольку проблема должна сходиться на этой сетке.

Начальная сетка (слева) и адаптированная сетка (справа) для модели потока Эйлера.

Адаптация для моделей, зависящих от времени

Адаптация для моделей, зависящих от времени, работает немного иначе. Грубая базовая сетка используется для продвижения решения в течение определенного интервала времени. Затем решение используется для уточнения сетки на основе некоторой индикаторной функции. Затем адаптированная сетка используется для повторного моделирования временного интервала. Ниже на левом изображении показана базовая сетка модели струйного сопла, а на среднем изображении показана адаптированная сетка.Поскольку это двухфазная модель, адаптация основана на \ | \ nabla \ phi \ |, где \ phi — функция установки уровня (0 в одной фазе и 1 в другой). Правое изображение показывает решение в конце временного интервала адаптации. Видно, как уточненная сетка перекрывает перенос фронта интерфейса на всем временном интервале.

Адаптация сетки в зависимости от времени для струйного сопла.

Адаптивное построение сетки по времени может быть очень экономичным методом получения отличных результатов.Эффективность сильно зависит от базовой сетки, которая не может быть слишком тонкой, поскольку проблема должна быть решена в течение дополнительного времени на базовой сетке. Если немного поработать над базовой сеткой, особенно с более сложной геометрией, то это часто окупается.

Заключительные замечания по инструментам построения сетки для моделей CFD

Создание хорошей сетки для задач CFD — это искусство. Даже при использовании адаптивной сетки высококачественная сетка является результатом понимания того, как работают различные инструменты создания сетки, и предвидения ожидаемого решения проблемы потока.

Первой создаваемой сетки редко бывает достаточно, и нам часто нужно изменить геометрию, сетку или и то, и другое. По этой причине полезны последовательности геометрии и построения сеток в COMSOL Multiphysics. Изменение, внесенное в последовательность геометрии, распространяется вниз по модели, поэтому нам не нужно повторно указывать физику или настройки сетки при внесении изменений в геометрию. Или мы можем существенно изменить настройки сетки и перестроить всю последовательность сетки, не начиная с нуля.Другая возможность — использовать параметры как в геометрии, так и в сетке и получить модель, в которой сетка может быть уточнена несколькими щелчками мыши.

Эта серия сообщений в блоге лишь поверхностно описывает возможности создания сеток в COMSOL Multiphysics. Настроек и опций намного больше, чем упомянутых здесь, и модели CFD могут извлечь из них большую пользу.