что это, значение, принцип работы
Тормозной путь автомобиля — это дистанция до полной остановки, которую успевает преодолеть машина с того момента, как водитель нажал педаль тормоза. Важно понимать, что остановочный путь всегда больше, чем тормозной. Ведь он включает еще и расстояние, пройденное с того момента, как водитель обнаружил опасность и нажал на тормоза.
Как рассчитать тормозной путь
Длина пути рассчитывается по следующей формуле:
l = V2/(2µg), где
l — путь,пройденный автомобилем;
V — скорость авто;
µ — коэффициент, определяющий силу трения
g — ускорение свободного падения (9,8м/с2).
Скорость легко определяется по показаниям спидометра, а коэффициент трения покрышек на сухом асфальте колеблется в диапазоне 0,5-0,8.
Для приблизительных расчетов используется µ=0,7.
Для скорости 60 км/час (по системе СИ — 16,7 м/с) тормозной путь равен:
16,72/(2*0,7*9,8)=20,24 метров.
Столько проедет серийная машина с момента начала торможения.
Однако такое значение актуально лишь для условий, приближенных к идеальным. При неравномерном срабатывании тормозов (цилиндров и колодок на каждом колесе) машина может потерять управляемость. Для восстановления контроля придется ослабить нажатие на тормоз. В этом случае тормозной путь будет значительно длиннее.
При расчете пройденного расстояния учитывается квадрат скорости. То есть, с ростом скорости тормозной путь резко удлиняется. При 80 км/час он составит уже 36 м, а на 120 км/час — 81 метр.
От чего зависит длина тормозного пути
Как видим, на тормозной путь влияют два параметра: скорость и коэффициент трения. Если скорость полностью зависит от действий водителя, то с трением все значительно сложнее. Давайте разберемся, какие факторы на расстояние, необходимое машине для остановки.
Состояние шин
Коэффициент сцепления (µ) зависит от следующих параметров:
Изношенный протектор сильно ухудшает торможение на мокрой, заснеженной или даже грязной дороге. Зато зависимость тормозного пути от температуры нелинейна.
Зато зависимость тормозного пути от температуры нелинейна.
При низких температурах резина теряет эластичность и коэффициент трения уменьшается. Поэтому в холодное время года нужно использовать зимние шины независимо от того, как успешно дорожные службы справляются с уборкой снега. Зимой даже на чистом асфальте тормозной путь на зимней резине будет намного короче, чем на летней.
При высоких температурах резина становится слишком мягкой. При этом она интенсивно изнашивается и начинает легче скользит по асфальту. Поэтому летом быстрее остановиться получится на летней резине, которая сохраняет эластичность, но не «течет» подобно пластилину.
Дорожное покрытие
Коэффициент трения, который на сухом асфальте равен 0.7, меняется в зависимости от погодных условий:
0,1 — гололед;
0,2 — снежный накат;
0,4 — мокрый асфальт.
В летнее время нужно остерегаться больших луж и грязи. Лужи могут вызвать эффект аквапланирования, при котором сцепление с дорогой будет даже хуже, чем на укатанном снегу. Не менее опасна и грязь: тонкий слой мокрой глины, практически невидимый глазом, делает асфальт таким скользким, что на нем становится сложно просто устоять на ногах.
Не менее опасна и грязь: тонкий слой мокрой глины, практически невидимый глазом, делает асфальт таким скользким, что на нем становится сложно просто устоять на ногах.
Антиблокировочная система
Как известно из школьного курса физики, сила трения скольжения всегда ниже, чем трения покоя. То есть, при торможении «юзом» тормозной путь больше. Этот эффект давно известен опытным водителями. Чтобы быстрее остановиться и не потерять управление на скользкой дороге, они используют «прерывистое» торможение. Метод заключается в том, что при блокировке колес водитель на мгновение отпускает педаль тормоза и тут же нажимает ее снова.
На большинстве современных серийных авто устанавливается электронная антиблокировочная система. Она контролирует вращение каждого колеса и снижает давление в тормозной магистрали при блокировке. В отличие от «прерывистого торможения», ABS контролирует каждый тормозной цилиндр в отдельности и ослабляет торможение только для заблокированных колес.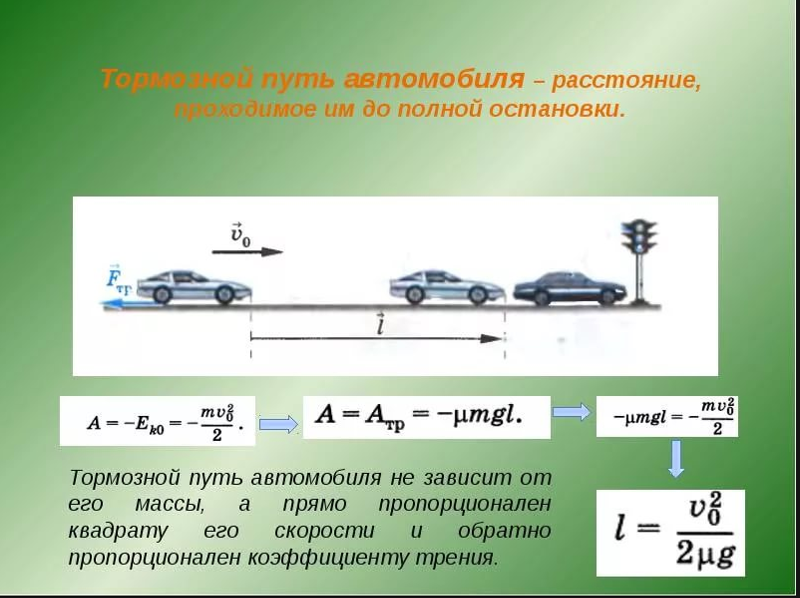 За счет этого удается достичь минимального тормозного пути на сухом асфальте, гололеде и мокрой дороге.
За счет этого удается достичь минимального тормозного пути на сухом асфальте, гололеде и мокрой дороге.
Однако антиблокировочная система не всегда позволяет остановить авто быстрее, чем торможение «юзом». На снегу и грязи она не позволяет протектору поглубже «зарыться» в дорогу. Особенно заметен эффект при использовании шипованной резины. Поэтому если вы хотите, чтобы шипы эффективно тормозили, «вгрызаясь» в снег, лед или грязь, ABS стоит отключить.
Калькулятор остановочного пути автомобиля • Механика • Онлайн-конвертеры единиц измерения
Калькулятор определяет остановочный путь автомобиля с момента обнаружения водителем опасности до момента полной остановки автомобиля, а также другие параметры, связанные с этим событием, в частности, время восприятия водителем сигнала о необходимости торможения, время реакции водителя, а также расстояние, которое прошел автомобиль во время этих событий. Калькулятор также определяет начальную скорость (скорость до начала торможения) по известной длине торможения (длины тормозного пути) с учетом дорожных условий. Как и все остальные калькуляторы, этот калькулятор не следует использовать в судебных процессах и при необходимости получения высокой точности.
Как и все остальные калькуляторы, этот калькулятор не следует использовать в судебных процессах и при необходимости получения высокой точности.
Пример 1: Рассчитать расстояние, необходимое для остановки автомобиля, движущегося со скоростью 90 км/ч по мокрой горизонтальной дороге с асфальтобетонным покрытием (коэффициент трения μ = 0,4) если время восприятия водителя 0,5 с и время реакции водителя 0,7 с.
Пример 2: Рассчитать начальную скорость автомобиля, движущегося по дороге с мокрым асфальтобетонным покрытием (μ = 0.4), если длина тормозного пути равна 100 м. Автомобиль движется на спуске с уклоном 10%.
Калькулятор остановочного пути
Входные данные
Начальная скорость
v0м/скм/чфут/смиля/ч
Время восприятия опасности водителем
thpс
Время реакции водителя
thrс
Уклон
σградус%
Движение вверх Движение вниз
Состояние дороги
—Сухой асфальтМокрый асфальтПокрытый снегом асфальтПокрытый льдом асфальтили Коэффициент трения
μ
Тип привода тормозов
—ПневматическийГидравлическийили Время срабатывания тормозной системы
tbrlс
Выходные данные
Угол крутизны уклона θ= °
Замедление a= м/с²
Время торможения tbr= с
Расстояние, которое проедет автомобиль во время восприятия водителем опасности Shp= м
Расстояние, которое проедет автомобиль во время реакции водителя на опасность Shr= м
Расстояние, которое проедет автомобиль за время задержки срабатывания тормоза Sbrl= м
Тормозной путь Sbr= м
Остановочный путь Sstop= м
Критический угол наклона для заданного коэффициента трения θcrit= °
Критический уклон для заданного коэффициента трения σcrit= %
Определения и формулы
Остановочный путь
Остановочный путь — это расстояние, которое проходит автомобиль с момента, когда водитель видит опасность, оценивает ее, принимает решение остановиться и нажимает на педаль тормоза и до момента полной остановки автомобиля. Это расстояние является суммой нескольких расстояний, которые проходит автомобиль в то время, как водитель принимает решение, срабатывают механизмы тормозной системы и происходит замедление движения до полной остановки.
Это расстояние является суммой нескольких расстояний, которые проходит автомобиль в то время, как водитель принимает решение, срабатывают механизмы тормозной системы и происходит замедление движения до полной остановки.
где shr — расстояние, которое проедет автомобиль во время восприятия и оценки водителем ситуации, shr — расстояние, которое проедет автомобиль во время во время реакции водителя на ситуацию, sbrl — расстояние, которое проедет автомобиль во время задержки срабатывания тормозов, и sbr — тормозной путь.
Расстояние, которое пройдет автомобиль во время восприятия и оценки водителем ситуации
Расстояние человеческого восприятия ситуации — это расстояние, которое пройдет автомобиль в то время, пока водитель оценивает опасность и принимает решение уменьшить скорость и остановиться. Оно определяется по формуле
где shp расстояние человеческого восприятия в метрах, v скорость автомобиля в км/ч, thp — время человеческого восприятия в секундах и 1000/3600 — коэффициент преобразования километров в час в метры в секунду (1 километр равен 1000 метров и 1 час равен 3600 секундам).
Расстояние, которое пройдет автомобиль во время реакции водителя
Расстояние реакции водителя — это расстояние, которое пройдет автомобиль пока водитель выполняет решение остановить автомобиль после оценки опасности и принятия решения об остановке. Оно определяется по формуле
где shp — расстояние реакции водителя с метрах, v — скорость автомобиля в км/ч и thr — время реакции водителя в секундах.
Расстояние, которое пройдет автомобиль во время срабатывания тормозной системы
Расстояние, которое пройдет автомобиль во время срабатывания тормозной системы, зависит от типа тормозной системы, установленной на автомобиле. Почти на всех легковых автомобилях и малотоннажных грузовых автомобилях используются гидравлическая тормозная система. На большинстве большегрузных автомобилей используются тормоза с пневматическим приводом. Задержка срабатывания пневматических тормозов приблизительно равна 0,4 с, а гидравлических (жидкость несжимаема!) 0,1–0,2 с. Общая задержка срабатывания тормозной системы измеряется как время от момента нажатия на педаль тормоза, в течение которого замедление становится устойчивым. Оно состоит из задержки срабатывания тормозной системы и времени установления постоянной величины замедления движения. В тормозной системе с пневматическим приводом воздуху необходимо время, чтобы пройти по тормозным магистралям. С другой стороны, в гидравлическом приводе задержек практически не наблюдается, и он работает в два—пять раз быстрее, чем пневматический.
Общая задержка срабатывания тормозной системы измеряется как время от момента нажатия на педаль тормоза, в течение которого замедление становится устойчивым. Оно состоит из задержки срабатывания тормозной системы и времени установления постоянной величины замедления движения. В тормозной системе с пневматическим приводом воздуху необходимо время, чтобы пройти по тормозным магистралям. С другой стороны, в гидравлическом приводе задержек практически не наблюдается, и он работает в два—пять раз быстрее, чем пневматический.
Расстояние, которое пройдет автомобиль во время срабатывания тормозной системы, определяется по формуле
где sbrl — расстояние в метрах, которое пройдет автомобиль во время срабатывания тормозной системы, v — скорость движения автомобиля в км/ч, tbrl — время срабатывания тормозной системы в секундах.
Замедление
Для упрощения расчетов предположим, что автомобиль движется с постоянным ускорением или замедлением, которое определяется по известной из курса элементарной физики формуле равноускоренного или равнозамедленного движения
где a — ускорение, v — начальная скорость, v0 — конечная скорость и t — время.
Тормозной путь автомобиля
Тормозной путь автомобиля — это расстояние, которое проходит автомобиль с момента полного нажатия на педаль тормоза до момента полной остановки. Это расстояние зависит от скорости автомобиля перед началом торможения и от коэффициента трения между шинами и дорожным покрытием. В этом калькуляторе мы не учитываем другие факторы, влияющие на тормозной путь, например, сопротивление качению шин или лобовое сопротивление воздуха
В результатах исследования1, в котором коэффициент трения определялся путем измерения замедления, определено, что антиблокировочная тормозная система (АБС) влияла на коэффициент трения таким образом: он увеличивается с увеличением скорости при использовании АБС и уменьшается, если АБС не используется. В этом исследовании также подтверждается, что на коэффициент трения между шинами и дорожным покрытием влияет температура и интенсивность дождя.
Вывод зависимости тормозного пути от скорости и трения с использованием второго закона Ньютона
Коэффициент трения определяется как отношения силы трения к силе нормального давления, прижимающей тело к опоре:
или
где Ffr — сила трения, μ коэффициент трения и Fnorm — сила реакции опоры.
Действующая на тело нормальная сила реакции опоры определяется как составляющая силы реакции, перпендикулярная к поверхности опоры тела. В простейшем случае, когда тело находится на плоской горизонтальной поверхности, нормальная сила равна весу этого тела:
где m — масса тела и g — ускорение свободного падения. Эта формула выведена из второго закона Ньютона:
В более сложном случае, если тело расположено на наклонной плоскости, нормальная сила рассчитывается как
где θ — угол наклона между плоскостью поверхности и горизонтальной плоскостью. В этом случае нормальная сила меньше веса тела. Случай наклонной поверхности мы рассмотрим чуть позже.
В случае же горизонтальной поверхности, если коэффициент трения между телом и поверхностью равен μ, то сила трения равна
В соответствии со вторым законом Ньютона, эта сила трения, приложенная к движущемуся телу (автомобилю) приводит к возникновению пропорционального ей замедления:
или
Теперь, в соответствии с уравнением ускоренного (замедленного) движения имеем
Из курса элементарной физики известно, что при равнозамедленном движении с постоянным замедлением, если конечная скорость равна нулю, то тормозной путь определяется уравнением
Это уравнение можно переписать в более удобной форме с использованием преобразования скорости в км/час в м/с:
Подставляя в это уравнение a = μg, получаем формулу тормозного пути:
где скорость v задается в км/час, а ускорение силы тяжести g в м/с².
Решая это уравнение относительно v, получаем:
Аналогичную формулу для определения тормозного пути можно получить с помощью энергетического метода.
Вывод зависимости тормозного пути от скорости и трения с помощью энергетического метода
Теоретическое значение тормозного пути можно найти, если определить работу по рассеиванию кинетической энергии автомобиля. Если автомобиль, движущийся со скоростью v, замедляет движение до полной остановки, работа тормозной системы Wb, требуемая для полного рассеяния кинетической энергии автомобиля Ek, равна этой энергии:
Кинетическая энергия движущегося автомобиля Ek определяется формулой
где m — масса автомобиля и v — скорость движения автомобиля перед началом торможения.
Работа Wb, выполненная тормозной системой, определяется как
где m — масса автомобиля, μ — коэффициент трения между шинами и дорожным покрытием, g — ускорение силы тяжести и sbr — тормозной путь, то есть расстояние, которое прошел автомобиль от начала торможения до полной остановки.
Теперь, с учетом того, что Ek = Wb, имеем:
или
Скорость автомобиля до начала торможения является наиболее важным фактором, влияющим на величину остановочного пути. Другими, менее важными, факторами, влияющими на остановочный путь, являются время оценки водителем ситуации, время реакции водителя, скорость работы тормозной системы автомобиля и состояние дороги.
Время торможения
Из курса элементарной физики известно, что средняя скорость при равноускоренном движении равна полусумме начальной и конечной скорости:
С учетом, что конечная скорость равна нулю, время торможения определяется в калькуляторе как
Движение вверх и вниз по уклону
Силы, действующие на автомобиль на уклоне: Fg — сила тяжести (вес автомобиля), Fgd — скатывающая вниз составляющая веса автомобиля, Ffr — сила трения, действующая параллельно поверхности дорожного полотна с уклоном, Fgn — нормальная составляющая веса автомобиля, направленная перпендикулярно поверхности дороги, и Fnr — сила реакции опоры, равная нормальной составляющей веса автомобиля.
Когда водитель нажимает на педаль тормоза, замедляющий движение автомобиль может быть представлен в виде тела на поверхности с углом наклона θ (см. рисунок выше). Для простоты мы будем рассматривать только две силы, действующие на автомобиль, находящийся на уклоне. Это вес автомобиля и сила трения. Автомобиль, движущийся с начальной скоростью, замедляет движение, если сила трения, действующая параллельно дорожному полотну, больше, чем скатывающая сила, являющаяся составляющей силы тяжести, которая также параллельна дорожному полотну. Если начальная скорость автомобиля равна нулю, он в этой ситуации остается на месте при условии, что угол уклона меньше критического (об этом — ниже).
В то время, как сила тяжести Fg стремится скатывать автомобиль вниз, сила трения Ffr сопротивляется этому движению. Чтобы автомобиль мог в этой ситуации остановиться, сила трения должна превышать скатывающую составляющую силы тяжести Fgd.
В то же время, если сила трения превышает скатывающую составляющую силы тяжести, автомобиль будет двигаться вниз с постоянным ускорением и его тормозная система будет неспособна его остановить. Это может произойти, если угол наклона (уклон) дорожного полотна слишком велик или коэффициент трения слишком мал (вспомним как ведет себя автомобиль с обычными шинами на уклоне, если он покрыт коркой льда!).
По определению коэффициента трения, можно записать уравнение для силы трения:
или
Скатывающая составляющая силы тяжести:
Результирующая сила Ftotal, действующая на автомобиль на уклоне:
или
Как мы уже отмечали, сила Ftotal должна быть направлена вверх, иначе автомобиль при движении вниз остановить невозможно. В соответствии со вторым законом Ньютона, ускорение (точнее, замедление) автомобиля, движущегося под действием силы Ftotal, определяется как
Подставляя ускорение в выведенную выше формулу тормозного пути, получаем:
Решая это уравнение для vpre-braking, получим:
Отметим еще раз, что в этих формулах g задается в м/с, v в км/ч и s в метрах. В нашем калькуляторе используются две последние формулы.
В нашем калькуляторе используются две последние формулы.
Припаркованные и движущиеся по ул. Дивисадеро в Сан-Франциско (Калифорния) автомобили. Уклон дорожного полотна в этом месте равен 31% или 17°.
Уклон
Величина уклона дороги (показателя крутизны склона) равна тангенсу угла плоскости дорожного покрытия к горизонтали. Он рассчитывается как отношение перпендикуляра, опущенного из точки на поверхность (превышения местности) к длине горизонтальной поверхности от начала склона до перпендикуляра (горизонтальному расстоянию). По определению уклона считается, что при движении вверх уклон является положительным, а при движении вниз уклон является отрицательным, когда превышение в действительности является понижением дороги. Уклон дороги σ выражают как угол наклона к горизонтали в градусах или как отношение в процентах. Например, подъёму 15 метров на 100 метров перемещения по горизонтали соответствует уклон, равный 0,15 или 15%. В этом калькуляторе мы используем уклон в процентах, определяемый по формуле
где Δh — превышение местности и d — проекция уклона на горизонталь (см. рисунок выше). Если известен уклон, то угол наклона можно определить по формуле
рисунок выше). Если известен уклон, то угол наклона можно определить по формуле
Критический угол
При увеличении угла наклона дорожного полотна выше определенного значения, называемого критическим углом, движущийся вниз автомобиль затормозить невозможно, так как действующая на него сила трения становится меньше скатывающей силы. Этот критический угол находится из условия
или
или
Из этой формулы можно найти критический угол для данного коэффициента трения, при котором автомобиль не сможет затормозить:
Уклон, выраженный в процентах, определяется по известному углу наклона таким образом:
Пример
В этом примере мы покажем, как использовать формулу для определения тормозного пути. Пусть автомобиль движется с начальной скоростью vpre-braking = 90 км/ч вниз по уклону σ = 5% по мокрому асфальту (коэффициент трения μ = 0,4). Нужно определить тормозной путь. Для расчетов используем выведенные выше формулы.
Особые случаи
Нажмите на соответствующую ссылку, чтобы посмотреть как работает калькулятор в особых режимах:
Литература
- Hartman, J 2014, Effects of velocity, temperature And rainfall on the friction coefficient of pneumatic tyres And bitumen roads, Doctor of Philosophy (PhD), Aerospace, Mechanical And Manufacturing Engineering, RMIT University PDF 48 MB
- Wikibooks. Fundamentals of Transportation
Автор статьи: Анатолий Золотков
Тормозной путь действительный — Энциклопедия по машиностроению XXL
Полный (расчётный) тормозной путь Действительный тормозной путь, равный полному пути за вычетом пути, пройденного во время подготовки тормозов к действию Путь, во время прохождения которого тормоза подготовляются к действиюПуть поршня, на интервале которого скорость поршня падает до нуля, называется условным тормозным путем л г- В действительности после включения тормозного устройства скорость хотя и резко падает, но не до нуля, а до некоторого значения, которое колеблется в определенных пределах до конца хода поршня Xj). [c.222]
[c.222]
Рассмотрим порядок определения тормозного пути. Тормозной путь St поезда складывается из подготовительного пути, который обозначается буквой Sn, и действительного пути торможения 5д, т. е. [c.77]
Действительный тормозной путь определяется по формуле S 50Q(ug— g) [c.78]
Теперь необходимо определить действительный тормозной путь. Для этой цели составим вспомогательную табл. 9 и определим расчетный коэффициент трения фкр тормозных колодок, удельное сопротивление состава Wo% и удельную тормозную силу г=1000 фкр р в интервале скоростей через 10 км/ч, причем в пределах каждого интервала надо будет брать их значения при средней скорости. [c.79]
Имея вспомогательную таблицу с необходимыми данными, определим действительный тормозной путь в каждом интервале скоростей аналитическим способом
[c. 80]
80]
Сложив тормозные пути, полученные в отдельных интервалах скоростей, определяем действительный тормозной путь [c.80]
Зная величину подготовительного и действительного тормозного пути, получим полный расчетный тормозной путь
Таким образом, тормозной путь s (м) поезда условно разделяется на две части подготовительная часть Sn, проходимая за время подготовки 1т , и остальная часть до остановки — действительный тормозной путь 5д [c.15]
В процессе прохождения поездом действительного тормозного пути изменяется скорость движения, в зависимости от скорости происходит изменение коэффициентов трения, тормозных сил и сил сопротивления движению. Поэтому действительный тормозной путь считают по интервалам изменения скорости, принимая постоянными действующие на поезд силы в рассматриваемом интервале. [c.15]
Общая величина действительного тормозного пути определяется как сумма путей, проходимых поездом за принятые интервалы изменения скорости (обычно не более чем по 10 км/ч)
[c. 15]
15]
Как рассчитывают подготовительный и действительный тормозной путь [c.17]
Полный тормозной путь St в м, т. е. расстояние, проходимее поездом от начала торможения до его остановки, состоит из пути подготовки к торможению и пути действительного торможения 5д тогда = Sn 5д. [c.33]
Действительный тормозной путь всегда больше теоретического, так как к времени торможения, за которое автомобиль проходит путь, добавляется еще время реакции водителя с момента обнаружения причины, требующей торможения, до нажатия на педаль, и время срабатывания тормозного привода. [c.122]
С нажатыми колодками от момента начала снижения скорости под действием тормозов до полной остановки поезд проходит путь, называемый действительным тормозным путем 8д. [c.180]
Таким образом, зная величину нетрудно вычислить и путь подготовки тормозов к действию по формуле (223).

Пользуясь графиком V = f(s) найдем тормозной путь при Он = 80 км/н. Для этого из точки Я кривой а = /( ) опускаем перпендикуляр на ось пути , который пересечет ее в точке Д. Отрезок О /С и есть пройденный путь заторможенным поездом при изменении скорости от н=80 км/ч до нуля. Это будет действительный путь торможения, ибо он определен при действии тормозной силы. Пользуясь масштабом пути у = 120 мм, находим, что д = [c.185]
Из последнего выражения видно, что при заданных значениях полного расчетного тормозного пути (в данном случае 8т= 1 ООО м) и спуска (( с = —Ю /оо) величины действительного пути торможения Яд зависят только от скорости Он, причем эта зависимость сложная, так. как тормозная сила 6т в свою очередь зависит от скорости. [c.185]
Для каждой из построенных кривых v= f(s), исходя из заданной величины расчетного тормозного пути Sj, строим в том же масштабе зависимость действительного тормозного пути 5д от скорости Vjj по способу, указанному в предыдущем параграфе.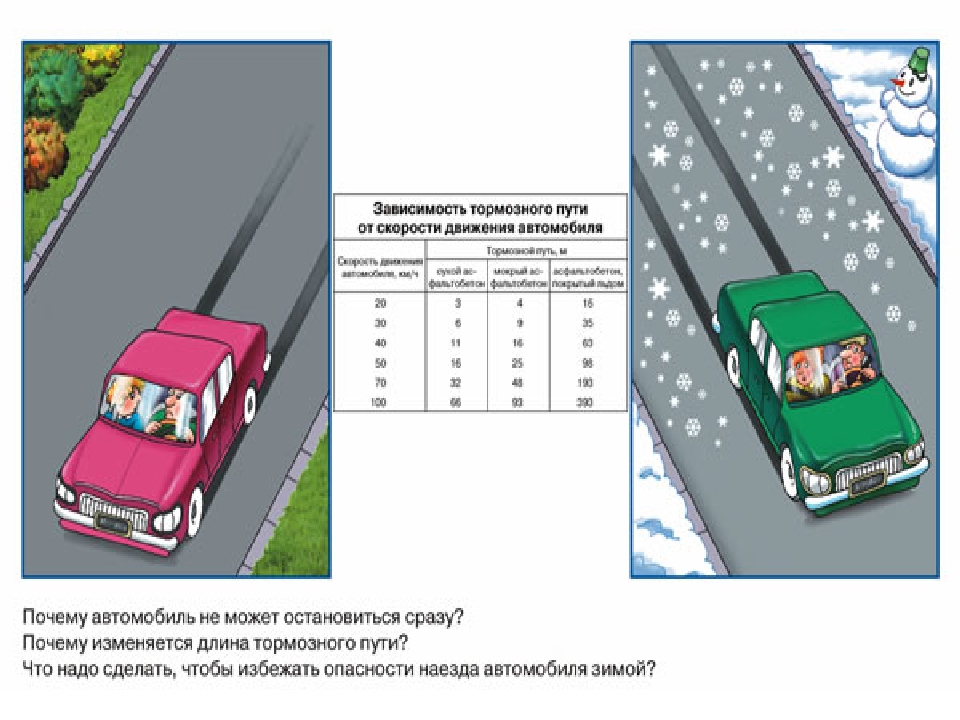 [c.189]
[c.189]
Если действительный тормозной путь отклоняется от расчетного более, чем на 25%, то необходимо произвести поверочный расчет, по результатам которого [c.300]
Так как распределение общей тормозной силы между Колесами не соответствует изменяющимся во время торможения нормальным реакциям на них, то действительный минимальный тормозной путь оказывается на 20—40% больше теоретического. С целью приближения результатов расчета к экспериментальным данным в формулы вводят коэффициент Кд, который учитывает степень использования полной теоретически возможной эффективности действия тормозной системы. Величина коэффициента эффективности торможения в среднем равна 1,2 для легковых автомобилей и
Тормозной путь, т. е. путь, проходимый поездом от начала торможения до остановки, определяют как сумму подготовительного пути п и действительного пути торможения 5д [c.318]
Действительный тормозной путь
[c.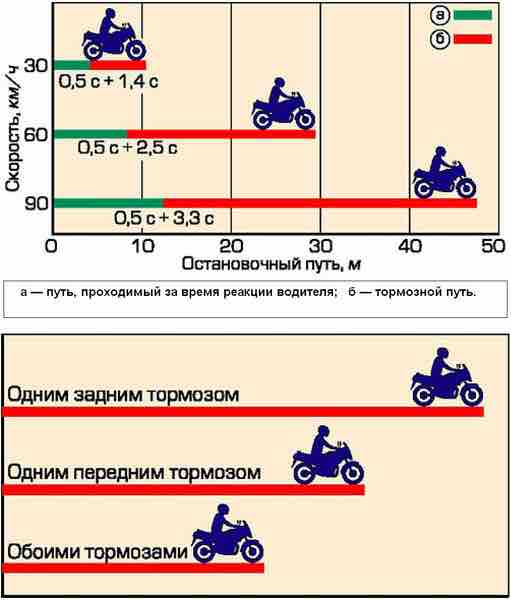 318]
318]
Тормозной путь при расчетах принимается равным сумме подготовительного тормозного пути и действительного пути торможения 5д. [c.128]
Действительный тормозной путь для интервала скоростей от v до Ок подсчитывают по формуле [c.129]
Приведенное аналитическое выражение для определения тормозного пути соответствует пути с момента полного включения тормозов. В действительных условиях с момента возникновения необходимости торможения до полного включения тормозов проходит некоторый промежуток времени, в течение которого действительная длина тормозного пути увеличивается. [c.720]
Как видно из сопоставления графиков, действительный тормозной путь превышает теоретические его значения. [c.723]
Полный тормозной путь—это путь, проходимый с момента начала торможения до остановки поезда и представляющий собой сумму действительного тормозного пути 5 и пути пду проходимого за время подготовки тормозов к действию
[c. 35]
35]
Действительный тормозной путь 5 —это расстояние, проходимое поездом за время, прошедшее от прижатия тормозных колодок до полной остановки. Считают, что за время [c.35]
При торможении поезда одним тепловозом подсчитывают действительный тормозной путь для интервала понижения скорости от Он до Ок по формуле [c.127]
На рис. 104, б показаны те же кривые (для М = 0,25), но полученные экспериментально. Все параметры здесь представлены в размерной форме. В идеальном случае скорость поршня должна достигать нулевого значения точно в момент прихода поршня в крайнее положение. Назовем тормозной путь, соответствующий этому случаю, условным и обозначим Хт в отличие от действительного тормозного пути Хг. [c.258]
Таким образом, действительная величина тормозного пути Хг в этом случае выбирается значительно больше его условного зна-260 [c.260]
Действительная длина тормозного пути, равная х = зХ , не зависит от величины рабочего хода поршня. Покажем это, заменив в уравнении (438) сначала 1 — X и затем 6
[c.266]
Покажем это, заменив в уравнении (438) сначала 1 — X и затем 6
[c.266]
Параметр X является некоторой предельной характеристикой работоспособности тормозного устройства. Если X занимает значительную часть хода, а это может оказаться при больших значениях М, то такого же порядка должен быть и действительный тормозной путь. Поэтому, если нас не удовлетворяет расчетная величина X, то, по-видимому, действительный тормозной путь [c.266]
Переход к размерным величинам совершается по формулам перехода. Ускорение х, как и длина тормозного пути 8г, не зависит от величины рабочего хода 8. Действительно, если все параметры пневмоустройства, кроме 5, остаются постоянными, то с изменением 5 величины Хо и X . изменяются в том же отношении, так как длина тормозного пути 5 от хода не зависит. Следовательно выражение, стоящее в квадратных скобках в правой части формулы (446), от 8 не зависит, и величина X будет изменяться про- [c.
 268]
268]Наибольшее влияние на время торможения оказывают следующие факторы начальная скорость поступательно движущихся частей, степень открытия тормозного дросселя и нагрузка на штоке. На характер перемещения большое влияние оказывает масса движущихся частей. В качестве примера на рис. П1 показаны осциллограммы привода с различными сечениями тормозного дросселя на выходе. Опыт проводился при следующих параметрах М = 0,16 т) = 0,11 Х = 0,05 Xj = 0,13 и при изменяющейся площади (fes) . Из сравнения осциллограмм можно видеть, как растет скорость поршня в момент конца хода с увеличением степени открытия дросселя и уменьшается время торможения. Очевидно также, что в первых трех случаях действительный тормозной путь является излишне большим. Тормозное устройство можно включить несколько позднее, при этом необходим запас на затухание колебаний скорости что касается последнего случая [c.277]
Действительно, сила трения скольжения при юзе фП меньше силы сцепления при качении фП, потому что коэффициент трения скольжения ф всегда меньше коэффициента трения покоя, определяющего величину г]), т.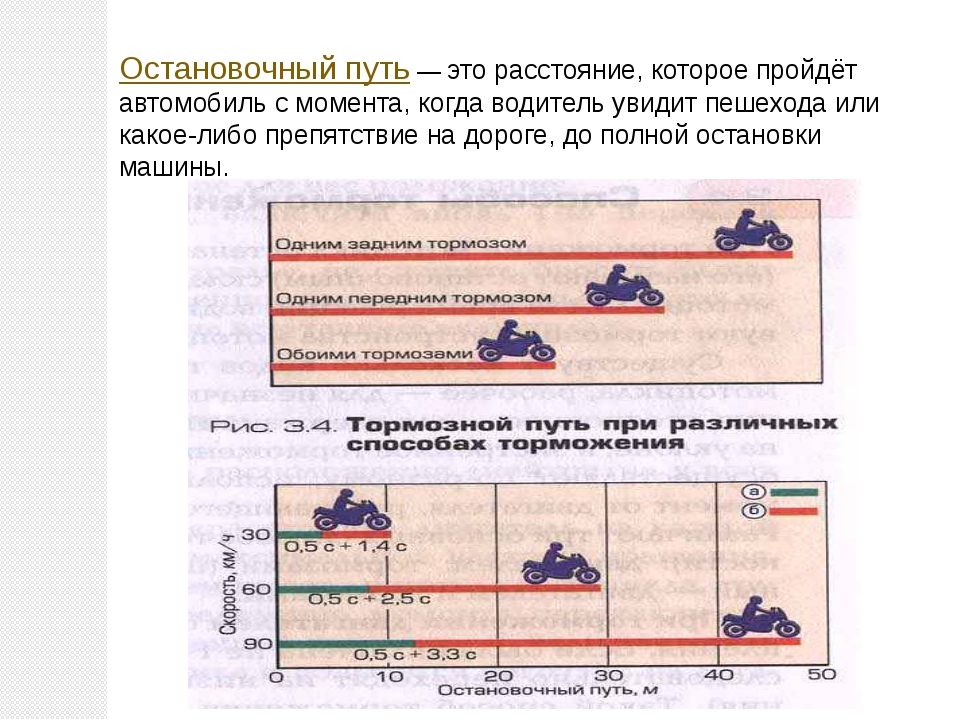 е. фП тормозной силы при качении. Вред юза — в увеличении тормозного пути, в изнашивании рельсов и образовании ползунов на ободах колес. Чтобы избежать этого, установлены технические условия надежного торможения при качении,, которые описываются неравенством
[c.225]
е. фП тормозной силы при качении. Вред юза — в увеличении тормозного пути, в изнашивании рельсов и образовании ползунов на ободах колес. Чтобы избежать этого, установлены технические условия надежного торможения при качении,, которые описываются неравенством
[c.225]
Тормозным путем называют расстояние, проходимое поездом от начала торможения до полной остановки. Он складывается из подготовительного 5п и действительного тормозного пути 5д, т. е. 5 = + 5д. [c.251]
Тормозной путь рассчитывается как сумма предтормозного пути и действительного тормозного пути. Условно принимается, что при проходе поездом предтормозного пути давления в тормозных цилиндрах нет, а затем в конце этого пути оно мгновенно возрастает до расчетного по линии d — с (рис. 20). [c.77]
Тормозной путь электропоезда делится на предтормоз-ной и действительный. [c.16]
Отсюда следует полный расчетный тормозной путь раЬен сумме пути подготовки тормозов к действию и действительного тормозного пути, т. е.
[c.181]
е.
[c.181]
Д 5д = ОсрД //3,6, а затем суммированием всех значений Д5д находят полный действительный тормозной путь. [c.127]
Следовательно, полный, или расчётный, тормозной путь 8 . равен сумме предтормозного пути и действительного тормозного пути 8д, т. е. [c.916]
Тормозной путь 5 при расчетах принимают равным сумме подготовительного пути (предтормозного) и действительного пути 5д торможения [c.11]
Разделение тормозного пути на 5 и 5д чисто условное и взято для упрощения расчетов в области неустановивш егося режима действия тормозной силы. Принимается, что за время прохождения поездом предтормозного пути тормоза в действие еще не пришли, а к концу предтормозного пути происходит мгновенное повышение тормозной силы до максимального значения, т. е. тормозная сила поезда повышается не постепенно, а мгновенно, спустя некоторое время, называемое временем подготовки. Таким условиям соответствует предположение, что наполнение воздухом тормозных цилиндров в поезде происходит не по действительной кривой АВ (рис. 8), а условно по прямой СД спустя некоторое время называемое временем подготовки.
[c.11]
8), а условно по прямой СД спустя некоторое время называемое временем подготовки.
[c.11]
ТОРМОЗНОЙ ПУТЬ — это… Что такое ТОРМОЗНОЙ ПУТЬ?
- ТОРМОЗНОЙ ПУТЬ
расстояние, пройденное трансп. машиной за время от начала торможения до полной остановки. Т. п. зависит от эффективности тормозных механизмов, времени срабатывания привода и тормозов, скорости движения, силы сцепления колёс с опорной поверхностью (дорога, рельсы и т. п.). См. рис.
К ст. Тормозной путь. График изменения тормозной силы РТ и замедления j автомобиля в процессе экстренного торможения: t1 — время реакции водителя; t2 — время запаздывания тормозного привода; t3 — время нарастания замедления; t4 — время полного торможения; t5 — время растормаживания. Тормозной путь соответствует времени t2 + t3 + t4
Большой энциклопедический политехнический словарь. 2004.
2004.
- ТОРМОЗНОЙ БАШМАК
- ТОРМОЗНОЙ ЩИТОК
Смотреть что такое «ТОРМОЗНОЙ ПУТЬ» в других словарях:
Тормозной путь — Тормозной путь расстояние, которое проходит транспортное средство с момента срабатывания тормозной системы до полной остановки. Протяжённость тормозного пути зависит от скорости, состояния проезжей части, шин, погодных условий. Особое… … Википедия
ТОРМОЗНОЙ ПУТЬ — расстояние, пройденное транспортной машиной от начала торможения до полной остановки. Зависит от эффективности тормозных механизмов, времени срабатывания привода и тормозов, скорости движения, силы сцепления колес с опорной поверхностью (дорога,… … Большой Энциклопедический словарь
ТОРМОЗНОЙ ПУТЬ — расстояние, проходимое поездом от начала торможения до полной остановки, с учетом также пути, проходимого за время от момента воспринятия сигнала до приведения в действие тормозов.
 При движении поезда по руководящему спуску длина Т. п.,… … Технический железнодорожный словарь
При движении поезда по руководящему спуску длина Т. п.,… … Технический железнодорожный словарьтормозной путь — 3.6 тормозной путь: Расстояние, пройденное вагоном с момента подачи команды на торможение до прекращения движения. Источник: ГОСТ Р 52232 2004: Вагоны легкого метро. Общие технические условия оригинал документа … Словарь-справочник терминов нормативно-технической документации
тормозной путь — расстояние, пройденное транспортной машиной от начала торможения до полной остановки. Зависит от эффективности тормозных механизмов, времени срабатывания привода и тормозов, скорости движения, силы сцепления колёс с опорной поверхностью (дорога,… … Энциклопедический словарь
Тормозной путь — расстояние, проходимое транспортным средством (автомобилем, поездом, трамваем и т.п.) от момента привода в действие тормозного устройства до полной остановки. Полный Т. п. (остановочный путь) включает в себя также расстояние, проходимое… … Большая советская энциклопедия
Тормозной путь — расстояние, пройденное транспортной машиной от начала торможения до полной остановки.
 Зависит от эффективности тормозных механизмов, времени срабатывания привода и тормозов, скорости движения, силы сцепления колес с опорной поверхностью (дорога,… … Автомобильный словарь
Зависит от эффективности тормозных механизмов, времени срабатывания привода и тормозов, скорости движения, силы сцепления колес с опорной поверхностью (дорога,… … Автомобильный словарьТормозной путь поезда — тормозной путь расстояние, проходимое поездом за время от момента воздействия на приборы и устройства для управления тормозной системой, в том числе срабатывания крана экстренного торможения (стоп крана), до полной остановки;… Источник:… … Официальная терминология
Тормозной путь высокоскоростного железнодорожного подвижного состава — тормозной путь расстояние, которое высокоскоростной железнодорожный подвижной состав проходит за время от момента воздействия на приборы и устройства для управления тормозной системы, в том числе срабатывания крана экстренного торможения, до… … Официальная терминология
тормозной путь поезда — тормозной путь поезда: Расстояние, проходимое поездом за время от момента воздействия на приборы и устройства для управления тормозной системой, в том числе срабатывания крана экстренного торможения (стоп крана), до полной остановки.
 [ГОСТ Р… … Словарь-справочник терминов нормативно-технической документации
[ГОСТ Р… … Словарь-справочник терминов нормативно-технической документации
Определение тормозного пути по номограммам
Номограммы длин тормозных путей (рис. 9.7) предварительно рассчитываются на ЭВМ численным интегрированием уравнения движения поезда, рассмотренным выше, и позволяют графически решать ряд следующих задач, связанных с торможением:
определение длины тормозного пути по известным значениям расчетного тормозного коэффициента и скорости движения;
определение необходимого расчетного тормозного коэффициента по заданным длине тормозного пути и скорости движения;
определение допустимой скорости движения по установленным длине тормозного пути и расчетному тормозному коэффициенту;
определение наибольшего значения спуска по известным расчетному тормозному коэффициенту, скорости движения и длине тормозного пути.
Большинство из приводимых в различных источниках номограмм (особенно относящихся к чугунным колодкам) рассчитывали для составов, имеющих до 200 осей.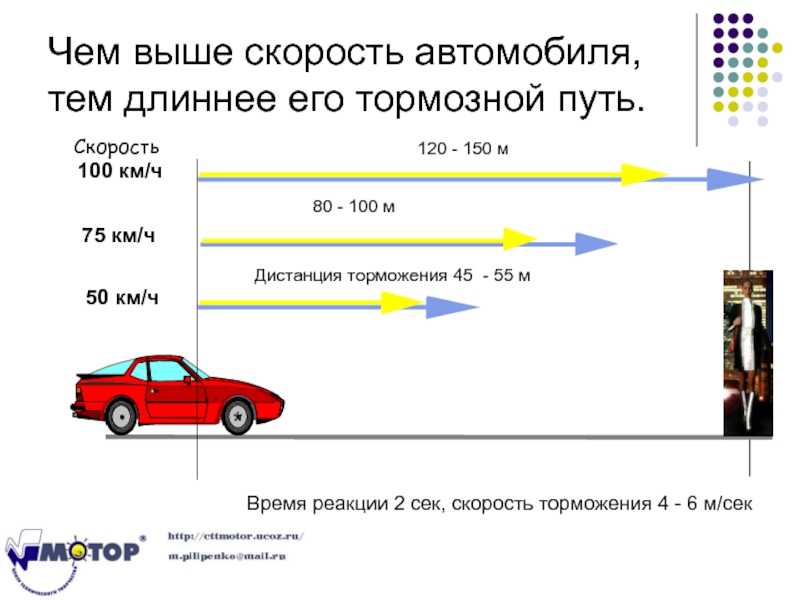 Однако их можно использовать и для расчета тормозного пути более длинных грузовых поездов. При этом расчетные коэффициенты при количестве осей до 300 и 400 уменьшаются соответственно на 10 и 15%.
Однако их можно использовать и для расчета тормозного пути более длинных грузовых поездов. При этом расчетные коэффициенты при количестве осей до 300 и 400 уменьшаются соответственно на 10 и 15%.
Если необходимо определить тормозной путь поезда на подъеме (до 10%о) с помощью номограмм, то нужно найти два его значения для заданных условий движения: на площадке и спуске, численно равном значению подъема. Затем вычесть из второго первый и полученную разницу вычесть из тормозного пути на площадке. В том случае, когда оценку тормозных характеристик требуется выполнить для промежуточных уклонов или скоростей, она производится для ближайших больших и меньших значений этих параметров и полученные результаты усредняются.
По номограммам для ЭТ можно находить тормозные пути при ПСТ, если уменьшить расчетный тормозной коэффициент поезда на 20 %.
Для снижения вероятности ошибки при графическом решении тормозных задач в последнее время номограммы заменяют таблицами, в которых расчетный тормозной коэффициент представлен с шагом 0,05, а скорость движения — 5 км/ч. Пример начала и конца такой таблицы (табл. 9.4) для определения длины тормозного пути приведен ниже [1].
Пример начала и конца такой таблицы (табл. 9.4) для определения длины тормозного пути приведен ниже [1].
В связи с большим количеством отличий в условиях торможения, таких, как категория поезда, тип используемых тормозных колодок, вид применяемых тормозов, величина уклона и т.д., полный набор номограмм для всех случаев подготовить весьма проблематично. Это ограничивает возможности их применения.
Доступность и высокий уровень развития вычислительной техники в настоящее время позволяют по разработанным программам расчета тормозного пути методом численного интегрирования по интервалам времени легко решить любую тормозную задачу. Ранее этот метод применялся как контрольный и наиболее универсальный для проверки точности расчетов, сделанных с помощью других методов.
Таблица 9.4
Длина тормозного пути грузового поезда, »=0 %
V, км/ч | Расчетный тормозной коэффициент | ||||||||||||
0,1 | 0,15 | 0,2 | 0,25 | 0^8 | 0,3 | 033 | 035 | 0,4 | 0,45 | 03 | 035 | 0,6 | |
10 | 38 | 32 | 29 | 27 | 26 | 26 | 25 | 25 | 24 | 24 | 23 | 23 | 23 |
15 | 74 | 60 | 52 | 48 | 46 | 45 | 43 | 42 | 41 | 40 | 39 | 38 | 37 |
120 | 530 | 380 | 298 | 247 | 225 | 212 | 196 | 186 | 167 | 151 | 139 | 129 | 120 |
⇐ | Расчет тормозного пути по интервалам времени | | Автоматические тормоза подвижного состава | | Расчет тормозного пути методом МРЖД | ⇒
Тормозной и остановочный пути автомобиля при скорости движения 90 и 130 км/ч
Главная | Энциклопедия автомобильных знаний
youtube.com/embed/q1gG9c88k-8?ecver=2&autohide=2″ frameborder=»0″ allow=»autoplay; encrypted-media» allowfullscreen=»» loading=»lazy»/>
Добро пожаловать на импровизированный тренинг по безопасному вождению от «Toyota Центр Минск Восток» и Центра контраварийной подготовки Сергея Овчинникова.
Сегодня рассмотрим вопрос как отличаются тормозной путь (с момента удара по педали тормоза до момента полной остановки) и остановочный путь (с момента возникновения препятствия, реакции водителя до остановки автомобиля) на скоростях движения 130 и 90 км/ч.
Какова же разница? Рассчитаем для безусловных случаев без привязки к автомобилю, дорожному покрытию, шинам — для одной и той же техники в разных условиях.
Торможение автомобиля — это рассеивание его кинетической энергии, набранной в процессе движения, превращение ее в тепловую энергию (разогрев тормозных колодок, тормозных дисков, шин и дорожного покрытия).
Формула работы сил торможения:
A = Fторм * Sторм = m(Vн)2/2 – m(Vк)2/2,
где A — работа сил торможения; Fторм — сила торможения, Sторм — тормозной путь; Vн — начальная скорость, Vк — конечная скорость, m — масса автомобиля.
Так как мы рассматриваем торможение до полной остановки, то Vк=0 и формула принимает вид:
A = Fторм * Sторм = mV2/2,
где V — начальная скорость движения.
Соответственно тормозной путь можно определить по формуле:
Sторм = mV2/(2*Fторм).
Как мы можем видеть, в числителе скорость движения возводится в квадрат. Мы можем сравнить 2 тормозных пути для одной и той же машины, с одной и той же массой, при одной и той же силе торможения (силе трения). Не будем учитывать аэродинамику автомобиля на разных скоростях и коэффициент трения в колодках и шинах в зависимости от скорости. Разница этих значений настолько мала, что мы можем ими пренебречь.
S130/S90 = (V130)2/(V90)2.
Разница в тормозных путях сводится к квадрату разницы между скоростями.
130 больше 90 примерно в 1,44 раза. Соответственно, 1,442=2,0736.
Таким образом тормозной путь до полной остановки при скорости движения 130 км/ч более чем в 2 раза больше, чем при движении со скоростью 90 км/ч.
А сколько же это в метрах? За основу возьмем результаты испытаний шин, в соответствии с которыми средний тормозной путь при скорости движения 90 км/ч составляет около 35 метров. Соответственно при 130 км/ч тормозной путь составит около 70 метров. Много это или мало? Попробуйте сделать примерно 100 шагов. Оцените это расстояние на глаз. Вы удивитесь, на сколько большим расстоянием вам покажется 35 метров. Обратите внимание, что это тормозной путь, а не остановочный.
Остановочный путь — это тормозной путь + расстояние, которое проедет автомобиль за некоторое время, которое требуется водителю для распознания ситуации и на принятие решения.
Среднестатистический водитель, который не является спортсменом-автогонщиком, по экспертным оценкам затрачивает на распознание ситуации и принятие решения примерно 1,5 сек. За это время автомобиль при скорости движения 90 км/ч проезжает 37,5 метров, а на скорости 130 км/ч — 54 метра. Таким образом, общий остановочный путь составит 35+37,5=72,5 и (35*2)+54=124 метров при 90 и 130 км/ч соответственно.
За это время автомобиль при скорости движения 90 км/ч проезжает 37,5 метров, а на скорости 130 км/ч — 54 метра. Таким образом, общий остановочный путь составит 35+37,5=72,5 и (35*2)+54=124 метров при 90 и 130 км/ч соответственно.
Разница впечатляющая! Теперь представьте, что экстренное торможение будет происходить ночью при дальности ближнего света фар 45–60 метров. Ехать ночью даже по идеальной дороге со скоростью 130 км/ч не зная, что ждет впереди, не видя полностью дороги — это более чем опасно. Очень много ДТП происходит именно по причине движения со скоростью, которая не соответствует безопасным условиям движения.
И это еще не все. Все расчеты выше актуальны при правильном выполнении экстренного торможения. Тормозной путь в 35 метров при скорости 90 км/ч получен на полигоне экспертами, которые умеют эффективного и правильно экстренно тормозить. Они при правильной посадке за рулем изо всех сил давят ногой на педаль тормоза, не боясь отдачи механизма ABS, и удерживают нажатой педаль до полной остановки. Практика на полигоне Центра контраварийной подготовки показывает, что единицы из сотни курсантов, не взирая на стаж вождения (водительский опыт), могут выполнить экстренное торможение. Большинство не умеет и не понимает, что это такое, а в автошколах, к сожалению, этому не обучают.
Пожалуйста, учитывайте описанные факты. Это очень важно для вашей жизни и здоровья, для безопасности дорожного движения.
Безопасных вам дорог!
02.05.2020
Дмитрий Перлин, тренер Тойота Центр Минск Восток и Lexus Минск, зам. директора Центра Контраварийной подготовки Сергея Овчинникова.
Мотосовет № 32 — Тормозной путь и время (простая математика)
Продолжаем переводить мотосоветы по теме «торможения». А какой торможение можно расматривать в отрыве от математики?Поэтому сегодня короткий урок простой математики по торможению!
James R Davis Stopping Distance And Time (The Math Is Simple)
Источник: http://msgroup.org/
Перевод: sixbisix
Один читатель после знакомства с Мотосоветом № 31 прислал мне небольшой критический комментарий:
Цитата:
В целом, все о чём вы написали правильно, но думаю вам вероятно нужно проверить ваши вычисления…
В арсенале дорожных строителей есть несколько эмпирических правил, выведенных с течением времени. Например, они установили, что если поверхность дороги сухая, то средний водитель может безопасно остановить автомобиль с замедлением 4.5 метра в секунду за секунду (м/сек/сек) (прим. Sixbisix — падение скорости составит 16 км/час за 1 сек). Это значит, что средний водитель может тормозить с таким замедлением, без какой-либо опасности потерять контроль над машиной.
Единицей измерения скорости является расстояние деленное на время (метры в секунду). Единицей измерения ускорения (или замедления в конкретном случае) являются метры/секунда/секунда в вашей интерпретации.
Я верю, что он хочет помочь, а не только потролить.
Даже если замедление измеряется в м/с/с, а не в м/с, то я не вижу проблем этом. В моей статье рассказывается о том, что вы можете «… замедлится… с замедлением 4.5 м/с», но я думаю, что из контекста понятно, что я имел ввиду, и независимо от скорости, предположим скорость перед торможением была 97 км/час, вы можете замедляться на 16.5 км/час каждую секунду, т.е. через 1 секунду ваша скорость будет 80 км/час, через 2 секунды 64 км/час и т.д. С математической точки зрения было бы корректнее говорить о «м/сек/сек», чем «м/сек», но возможно это бы кого-нибудь запутало.
[Инженеры обычно в своих расчётах используют замедление 16 км/час/сек, указанное в «Стандарт геометрического дизайна скоростных магистралей и улиц» (страница 111). Как следует из цитаты ниже, со страницы 111, это очень консервативное значение:]
(Прим. SixBiSix: в оригинале цитата со страницы 111 пропущена)
Вы заметите, что там сказано «большинство водителей замедляются с замедлением выше 16 км/час/сек» и это с учётом того, что 90% водителей могут замедляться быстрее 12 км/час/сек.
Далее в письме мой читатель продолжает рассуждать:
Цитата:
Это значит, что вы можете остановить ваш мотоцикл за 5.4 секунды (включая 1 секунду на задержку) и общая длинна остановочного пути будет всего 86 метров!
Если вы посмотрите на любой дорожный тест современного мотоцикла, то увидите, что тормозной путь со скорости 97 км/час составляет обычно 37-43 метра. Часто разброс составляет 46-55 метров.
Основываясь на этом предположении, я перепроверил математически и получил такие же результаты.
Здесь я не вижу никаких несоответствий. Смысл мотосовета был в том, что повышая свой навык торможения, вы значительно уменьшаете как время остановки так и остановочный путь. Более того, хотя я осознаю, что мотогонщик может достигнуть замедления 1g (35 км/час/сек) или больше, достаточно опытный мотоциклист может легко тормозить с замедлением более 21 км/час/сек. Для сравнения дорожные строители исходят из предположения, что средний водитель безопасно может достигнуть замедления 16 км/час/сек.
Поэтому, я не говорил, что вы должны (или можете) тормозить с замедлением 1g. Я имел ввиду, что вы, если немного потренируетесь, можете и должны стремиться к тому, чтобы тормозить намного лучше (безопаснее) «усреднённого водителя».
Вернемся к расчётам…
Для того, чтобы определить время торможения при постоянном замедлении, вы должны просто разделить скорость перед началом торможения (в км/час) на величину замедления.
96.56 км/час=26.82 м/сек. Если вы тормозите с замедлением в 6.09 м/сек/сек, то время остановки составит = 29/6=4.4 сек. Еще 1 секунда на задержку перед началом торможения (распознавание опасности и время реакции) и всего для остановки потребуется 5.4 секунды. Столько сколько я и говорил.
Для того, чтобы определить остановочный путь вы должны ½ скорости перед торможением умножить на время торможения (т.е. вы определите вашу среднюю скорость при торможении и умножите её на время, в течение которого вы тормозили). Для приведенного выше примера порядок вычислений следующий:
0.5*26.82*4.4= 59 метра. Так как мы проехали 26.82 метра перед тем, как нажали на тормоза, то мы прибавляем это расстояние к 59 метрам и в итоге получаем 85.82 метра. Столько, сколько я говорил.
Почему же результаты моих вычислений так далеки от данных производителя? Ответ прост. Они указывают ТОЛЬКО тормозной путь и замедление в 1g. [Журнал «Ездок» как-то опубликовал результаты замеров остановки мотоцикла Yamaha со скорости 96.56 км/час. Средний результат 56.99 метров в серии из 9 попыток. Это значит, что торможение было с замедлением 13.41 м/сек или примерно 1.3g ]
Принимая замедление равное 9.75 м/сек (1g) мы вычисляем время остановки 2.75 секунды (26,82/9,75). Рассчитанный тормозной путь составит 36.87 метра (Не принимая во внимание дополнительные 26.82 метра, которые проедет мотоцикл до начала торможения). Это соответствует данным, опубликованным в отчёте.
Математика – это просто. Вывод тоже прост – умелое торможение может сохранить вашу жизнь.
Для тех, кто силён в математике. Я полностью осознаю, что когда я упростил уравнение и ввел понятие «средней скорости», то в итоге получил лишь приблизительный тормозной путь. Формула для точных вычислений, которая учитывает замедление, может быть трудна для восприятия некоторыми читателями. Я решил упростить эту формулу потому, что смысл её прост (Кроме того она дает точно такой же результат).
где,
X – остановочный путь (метры)
Xо – путь до начала торможения (метры – например, распознавание и начало действия – расстояние 26 метров)
Vо – первоначальная скорость (м/сек)
t – время торможения (секунды)
a – замедление (м/с/с)
P.S. cophia куда-то пропала 🙁 Поэтому пока мотосовет без её картинки… :_(
Расчет тормозного пути — Движение транспортных средств — Edexcel — GCSE Physics (Single Science) Revision — Edexcel
Важно уметь:
- оценить, как тормозной путь транспортного средства изменяется в зависимости от скорости
- Расчет работы выполнено при остановке движущегося транспортного средства
На диаграмме показаны некоторые типичные тормозные пути для среднего автомобиля в нормальных условиях.
Важно отметить, что расстояние мышления пропорционально начальной скорости.Это потому, что время реакции принято как постоянное, а расстояние = скорость × время. {2} \]
Итак, при фиксированной максимальной тормозной силе тормозной путь пропорционален квадрату скорости.
Пример расчета дистанции мышления
Автомобиль движется со скоростью 12 м / с. Водитель имеет время реакции 0,5 с и видит, что впереди на дорогу выбегает кошка. На каком расстоянии мыслить водитель?
расстояние = скорость × время
\ [d = v \ times t \]
\ [d = {12} \\ м / с \ times {0,5} \\ s \]
\ [мышление \\ distance = 6 \ m \]
Пример расчета тормозного пути
Автомобиль в предыдущем примере имеет общую массу 900 кг.{2}} {2,000} \]
\ [braking \ distance = 32 \ m \]
Пример расчета тормозного пути
Каков тормозной путь для автомобиля выше?
тормозной путь = расстояние мысли + тормозной путь
тормозной путь = 6 + 32
тормозной путь = 38 м
- Вопрос
Рассчитайте тормозной путь для автомобиля и водителя в приведенном выше примере, когда движется со скоростью 24 м / с.
- Показать ответ
\ [мышление \ расстояние = 24 \ м / с \ умножить на 0.{2}} {100} \]
тормозное усилие ~ 87 000 Н
Знаете ли вы, как рассчитать тормозной путь?
Что такое тормозной путь?
Тормозной путь — это расстояние до остановки автомобиля после нажатия на педаль тормоза.
Расчет тормозного пути важен для предотвращения потенциальных аварий или опасных ситуаций.
Факторы, влияющие на расстояние
Существует множество переменных факторов, которые могут повлиять на то, как долго ваш автомобиль останавливается.Вот некоторые;
- Скорость транспортного средства
- Вес транспортного средства
- Дорожные условия (скользкий, ледяной, снег, сухой, мокрый)
- Условия тормозов транспортного средства (старые или изношенные колодки и роторы)
- Тормозная техника в транспортном средстве (например, как ABS)
- Состояние шин (лысые шины)
Это приводит нас к фактической формуле для расчета тормозного пути.
Формула основана на скорости (скорости) транспортного средства и коэффициенте трения между колесами и дорогой.
Тормозной путь = скорость² / 2 (коэффициент трения) (гравитационное ускорение)
Да, в любом случае, как только олень выбегает перед вами, вы думаете: «Итак, сколько 50 миль в час в квадрате… деленное на ..? » splat.
Хорошо, это не работает. Если вы не гений физики или математики, это нереально.
Вот несколько более простая формула, опубликованная на сайте инструктора по вождению Майкла Никсона.
Предполагается, что сухая погода и хорошее покрытие.
20 миль / ч = x2 = 40 футов
30 миль / ч = x2,5 = 75 футов
40pmh = x3 = 120 футов
50 миль / ч = x3,5 = 175 футов
60 миль / ч = x4 = 240 футов
70 миль / ч = x4,5 = 315 футов
Удвоить (X2) эти расстояния для мокрой дороги, и умножить на десять ( X10) для снег / лед .
Рассчитайте тормозной путь EASY WAY.
Это не тормозной путь, но хорошее место для старта.
По версии Smartmotorist.com следует применить « правило трех секунд ». Это означает, что вы найдете неподвижный объект на обочине дороги, например, дорожный знак или отметку мили.
Когда впереди идущий автомобиль проезжает знак, сосчитайте до трех, и к этому времени вы уже проезжаете тот же дорожный знак / объект, который выбрали.
На скорости 65 миль в час вы можете проехать почти 100 футов в секунду.
Правило трех секунд должно дать вам расстояние около 288 футов между движущимся впереди автомобилем.
Это основано на хороших сухих условиях. Увеличьте количество секунд для мокрой дороги и ненастной погоды.
Дважды для мокрой дороги (6 секунд) и десять раз для снега (30 секунд).
Соблюдайте безопасную дистанцию следования ». Соблюдайте безопасную дистанцию следования (правило трех секунд) . Умный автомобилист, н.о. Интернет. 21 апреля 2017 г.
Никсон, Майкл.«Простой способ рассчитать тормозные пути». Простой способ выработать тормозные пути | Майк Никсон . N.p., n.d. Интернет. 21 апреля 2017 г.
Остановка и тормозной путь в физике — видео и стенограмма урока
Расстояние мышления (TD)
Давайте сначала начнем с расстояния мышления (TD), которое показано в уравнении 2. Скорость автомобиля можно представить как постоянную в течение короткого промежутка времени, необходимого для реакции водителя, поэтому все, что мы Чтобы получить расстояние мышления, нужно умножить скорость на время реакции.Поскольку время реакции человека, желающего затормозить, обычно меньше секунды, это расстояние является наименьшим по отношению к тормозному пути.
Тормозной путь (BD)
Вывести уравнение для тормозного пути немного сложнее. Начнем с кинематического уравнения, показанного в уравнении 3.
Где:
- vf = конечная скорость
- vo = начальная скорость
- a = ускорение
- d = пройденное расстояние
Мы знаем, что конечная скорость равна нулю, потому что машина остановилась.Единственное неизвестное в этом уравнении — это ускорение a . Автомобиль замедляется (ускоряется в направлении, противоположном его движению), потому что на него действует неуравновешенная сила.
Тормоза создают трение колесам, замедляя их, но статическое трение ( f ) между колесами и дорогой в конечном итоге останавливает машину. Сопротивление воздуха и трение качения участвуют, но в меньшей степени. Вес автомобиля ( мг, ) и нормальная сила ( Н, ) являются вертикальными силами, и они равны.Схема свободного тела показана на Диаграмме 1.
Второй закон Ньютона используется для расчета ускорения автомобиля. Трение рассчитывается путем умножения коэффициента трения (μ) на нормальную силу ( Н, ).
f = μ N
Нормальная сила составляет мг , потому что она должна только противодействовать весу автомобиля. Последняя строка в уравнении 4 дает нам ускорение автомобиля.
Теперь мы можем подставить ускорение, которое мы только что определили, в уравнение 3, чтобы получить уравнение тормозного пути, BD. Давайте рассмотрим это более подробно.
Последний шаг в нашем выводе уравнения тормозного пути (SD) — это прибавить мысленное расстояние (TD) к тормозному пути (BD), что показано в уравнении 6.
Давайте представим, что время реакции нашего водителя составляет 0,5 с, и мы знаем, что начальная скорость составляет 73 км / ч, что составляет 20,3 м / с. Коэффициент трения (μ) можно оценить как 0,8, что является средним значением для резиновых шин на сухом бетоне. Что теперь может определить наш минимальный тормозной путь?
Довольно удивительно, что за доли секунды наш мозг может сравнить значение тормозного пути с нашей оценкой того, как далеко мы от перекрестка, и принять решение, остановиться или проехать перекресток.Что ж, может быть, это не совсем то, что происходит, но с практикой вождения мы обучаемся точно оценивать расстояние, которое нам нужно, чтобы остановиться, в зависимости от нашей скорости.
Дальность мышления увеличивается со скоростью. Время нашей реакции может быть постоянным, но умножение его на все более и более высокие скорости увеличивает расстояние мышления с увеличением скорости. Тормозной путь увеличивается экспоненциально с увеличением скорости, потому что начальная скорость автомобиля возведена в квадрат в уравнении тормозного пути.Например, для остановки движения со скоростью 20 м / с требуется дополнительно 24 м по сравнению с 10 м / с. График 1 показывает тормозной путь в сравнении с начальными скоростями.
Резюме урока
Давайте сделаем несколько минут, чтобы повторить то, что мы узнали!
Каждый раз, когда кто-то водит машину, он должен в какой-то момент остановить ее. Это включает в себя принятие решения об остановке, во время которого автомобиль проезжает определенное расстояние, равное его мгновенной скорости, умноженной на время реакции водителя.Мы называем это расстояние расстоянием мышления (TD). Это кратчайшее расстояние в уравнении тормозного пути, потому что время реакции водителя очень мало.
Тормозной путь (BD) — это расстояние, необходимое для остановки после включения тормозов, а статическое трение между шинами и дорогой является доминирующей тормозящей силой, замедляющей автомобиль до полной остановки.
Сложение этих двух расстояний вместе дает нам тормозной путь (SD).
Самым большим фактором при оценке этого расстояния является скорость автомобиля, поскольку она возведена в квадрат в уравнениях тормозного пути и тормозного пути.
Случайный преобразователь | Онлайн-конвертеры единиц измеренияКонвертер длины и расстоянияКонвертер массыКонвертер сухого объема и общих измерений при приготовлении пищиПреобразователь площадиПреобразователь объема и общих измерений при приготовленииПреобразователь температурыПреобразователь давления, напряжения, модуля ЮнгаПреобразователь энергии и работыПреобразователь силыПреобразователь силыКонвертер времениЛинейный конвертер скорости и скоростиКонвертер углового расходаПреобразователь топливной эффективности, расхода топлива и информации о расходе топливаПреобразователь единиц Хранение данныхКурсы обмена валютЖенская одежда и размеры обувиМужская одежда и размеры обувиКонвертер угловой скорости и частоты вращенияКонвертер ускоренияКонвертер углового ускоренияКонвертер плотностиКонвертер удельного объемаПреобразователь момента инерцииПреобразователь момента силыКонвертер крутящего моментаПреобразователь удельной энергии, теплоты сгорания (на единицу температуры) Преобразователь интерваловКонвертер коэффициента теплового расширенияПреобразователь теплового сопротивленияПреобразователь теплопроводности Конвертер удельной теплоемкости terПлотность тепла, плотность пожарной нагрузкиКонвертер плотности теплового потокаПреобразователь коэффициента теплопередачиКонвертер объемного расходаПреобразователь массового расходаМолярный расходомерКонвертер массового потока Конвертер скорости передачиКонвертер уровня звукаКонвертер чувствительности микрофонаКонвертер уровня звукового давления (SPL) Конвертер уровня звукового давления с выбираемым эталонным давлениемКонвертер яркостиКонвертер яркостиКонвертер яркостиКонвертер разрешения цифрового изображенияПреобразователь частоты и длины волныОптическая мощность (диоптрия) в преобразователь фокусного расстоянияПреобразователь оптической мощности (диоптрия) в увеличение (X) Конвертер электрического заряда Конвертер плотности зарядаКонвертер поверхностной плотности зарядаКонвертер объёмной плотности заряда Конвертер электрического токаЛинейный преобразователь плотности токаПреобразователь плотности поверхностного токаПреобразователь напряженности электрического поляПреобразователь электрического потенциала и напряженияПреобразователь электрического сопротивленияПреобразователь электрического сопротивленияПреобразователь электрической проводимостиПреобразователь электрической проводимостиПреобразователь емкостиПреобразователь индуктивностиПреобразователь реактивной мощности переменного токаПреобразователь единиц магнитного поля в ваттах и дБм Конвертер плотности потока Конвертер мощности поглощенной дозы излучения, Конвертер мощности дозы полного ионизирующего излученияРадиоактивность.Конвертер радиоактивного распада Конвертер радиоактивного облученияРадиация. Конвертер поглощенной дозы Конвертер метрических префиксов Конвертер передачи данных Конвертер единиц типографии и цифрового изображения Конвертер единиц измерения объема древесиныКалькулятор молярной массыПериодическая таблица Этот онлайн-конвертер единиц измерения позволяет быстро и точно переводить многие единицы измерения из одной системы в другую. Страница преобразования единиц представляет собой решение для инженеров, переводчиков и для всех, чья деятельность требует работы с величинами, измеренными в различных единицах. Вы можете использовать этот онлайн-конвертер для преобразования нескольких сотен единиц (включая метрическую, британскую и американскую) в 76 категорий или нескольких тысяч пар, включая ускорение, площадь, электрическую энергию, энергию, силу, длину, свет, массу, массовый расход, плотность, удельный объем, мощность, давление, напряжение, температура, время, крутящий момент, скорость, вязкость, объем и емкость, объемный расход и многое другое. Преобразователи общих единицКонвертер длины и расстояния : метр, километр, сантиметр, миллиметр, нанометр, ярд, фут, дюйм, парсек, световой год, астрономическая единица, расстояние до Луны (от Земли до Луны), лига , миля, морская миля (международная), сажень, длина кабеля (международная), точка, пиксель, калибр, планковская длина… Конвертер массы : грамм, килограмм, миллиграмм, тонна (метрическая), фунт, унция, камень (США), камень (Великобритания), карат, зерно, талант (библейский греческий), драхма (библейский греческий), денарий (библейский римский), шекель (библейский иврит), масса Планка, масса протона, атомная единица массы, масса электрона (покой), масса Земли, масса Солнца … Объем сухого вещества и стандартные измерения при приготовлении пищи : литр, бочка сухой (США), пинта сухой (США), квартовый сухой (США), peck (США), peck (Великобритания), bushel (США), bushel (UK), cor (библейский), homer (библейский), ephah (библейский) ), seah (библейский), omer (библейский), cab (библейский), log (библейский), кубометр. Конвертер площади : миллиметр², сантиметр², метр², километр², гектар, акр, дюйм², фут², ярд², миля², сарай, круглый дюйм, поселок, род, стержень², окунь², усадьба, шест², сабин, арпент, куерда, квадратная верста, квадратный аршин, квадратный фут, квадратный сажень, площадь Планка … Конвертер объёма и общепринятых единиц измерения температуры : метр³, километр³, миллиметр³, литр, гектолитр, миллилитр, капля, бочка (масло), бочка (США) ), баррель (Великобритания), галлон (США), галлон (Великобритания), кварта (США), кварта (Великобритания), пинта (США), пинта (Великобритания), баррель (нефть), баррель (США), баррель (Великобритания ), галлон (США), галлон (Великобритания), кварта (США), кварта (Великобритания), пинта (США), пинта (Великобритания), ярд³, фут³, дюйм³, регистровая тонна, 100 кубических футов… Преобразователь температуры : кельвин, градус Цельсия, градус Фаренгейта, градус Ренкина, градус Реомюра, температура Планка. Преобразователь давления, напряжения, модуля Юнга : паскаль, килопаскаль, мегапаскаль, миллипаскаль, микропаскаль, нанопаскаль, техническая атмосфера, стандартная атмосфера, ksi, psi, ньютон / метр², бар, миллибар, килограмм-сила / метр², грамм- сила / сантиметр², тонна-сила (короткая) / фут², фунт-сила / фут², миллиметр ртутного столба (0 ° C), дюйм ртутного столба (32 ° F), сантиметр водяного столба (4 ° C), фут водяного столба (4 ° C) , метр морской воды… Конвертер энергии и работы : джоуль, килоджоуль, мегаджоуль, миллиджоуль, мегаэлектронвольт, электрон-вольт, эрг, киловатт-час, мегаватт-час, ньютон-метр, килокалория (IT), калория (пищевая), Британские тепловые единицы (IT), мегабтеки (IT), тонна-час (охлаждение), тонна нефтяного эквивалента, баррель нефтяного эквивалента (США), мегатонна, тонна (взрывчатые вещества), килограмм в тротиловом эквиваленте, дин-сантиметр, грамм-сила-сантиметр, килограмм-сила-метр, килопонд-метр, фут-фунт, дюйм-фунт, энергия Планка … Преобразователь мощности : ватт, киловатт, мегаватт, милливатт, лошадиные силы, вольт-ампер, ньютон-метр / секунда, джоуль / секунда, мегаджоуль в секунду, килоджоуль в секунду, миллиджоуль в секунду, джоуль в час, килоджоуль в час, эрг в секунду, британские тепловые единицы (IT) в час, килокалорий (IT) в час… Преобразователь силы : ньютон, килоньютон, миллиньютон, дин, джоуль / метр, джоуль / сантиметр, грамм-сила, килограмм-сила, тонна-сила (короткая), кип-сила, килопунт-сила, фунт-сила сила, унция-сила, фунтал, фунт-фут в секунду², pond, sthene, грав-сила, миллиграв-сила … Преобразователь времени : секунда, миллисекунда, наносекунда, пикосекунда, минута, час, день, неделя, месяц, год, декада, век, тысячелетие, планковское время, год (юлианский), год (високосный), год (тропический), год (сидерический), год (григорианский), две недели, встряска… Конвертер линейной скорости и скорости : метр в секунду, километр в час, километр в секунду, миля в час, фут в секунду, миля в секунду, узел, узел (Великобритания), скорость света в вакууме, космический скорость — первая, космическая скорость — вторая, космическая скорость — третья, скорость Земли, скорость звука в чистой воде, Мах (стандарт СИ), Мах (20 ° C и 1 атм), ярд / секунду … Угол Преобразователь : градус, радиан, град, гон, минута, секунда, знак, мил, оборот, круг, поворот, квадрант, прямой угол, секстант. Конвертер топливной экономичности, расхода топлива и экономии топлива : метр / литр, километр / литр, миля (США) / литр, морская миля / литр, морская миля / галлон (США), километр / галлон (США), литр / 100 км, галлон (США) / миля, галлон (США) / 100 миль, галлон (Великобритания) / миля, галлон (Великобритания) / 100 миль … Конвертер чисел : двоичный, восьмеричный, десятичный, шестнадцатеричный, основание-3, основание-4, основание-5, основание-6, основание-7, основание-9, основание-10, основание-11, основание-12, основание-13, основание-14, основание-15, основание-20, основание-21, основание-22, основание-23, основание-24, основание-28, основание-30, основание-32, основание-34, основание-36… Преобразователь единиц информации и хранения данных : бит, байт, слово, четверное слово, MAPM-слово, блок, килобит (10³ бит), кибибит, кибибайт, килобайт (10³ байтов), мегабайт (10⁶) байтов), гигабайт (10⁹ байтов), терабайт (10¹² байтов), петабайт (10¹⁵ байтов), эксабайт (10¹⁸ байтов), гибкий диск (3,5 ED), гибкий диск (5,25 HD), Zip 250, Jaz 2 ГБ, CD (74 минут), DVD (2 слоя 1 сторона), диск Blu-ray (однослойный), диск Blu-ray (двухслойный) … Курсы обмена валют : евро, доллар США, канадский доллар, британский фунт стерлингов, японская иена, швейцарский франк, аргентинское песо, австралийский доллар, бразильский реал, болгарский лев, чилийское песо, китайский юань, чешская крона, датская крона, египетский фунт, венгерский форинт, исландская крона, индийская рупия, индонезийская рупия, новый израильский шекель , Иорданский динар, малайзийский ринггит, мексиканское песо, новозеландский доллар, норвежская крона, пакистанская рупия, филиппинское песо, румынский лей, российский рубль, саудовский риял, сингапурский доллар, Южноафриканский рэнд, южнокорейский вон, шведская крона, новый тайваньский доллар, тайский бат, турецкая лира, украинская гривна… Размеры женской одежды и обуви : женские платья, костюмы и свитера, женская обувь, женские купальные костюмы, размер букв, бюст, дюймы, естественная талия, дюймы, заниженная талия, дюймы, бедра, дюймы, бюст, сантиметры, Натуральная талия, сантиметры, Заниженная талия, сантиметры, Бедра, сантиметры, Длина стопы, мм, Торс, дюймы, США, Канада, Великобритания, Европа, континентальный, Россия, Япония, Франция, Австралия, Мексика, Китай, Корея .. Размеры мужской одежды и обуви : мужские рубашки, мужские брюки / брюки, размер мужской обуви, размер букв, шея, дюймы, грудь, дюймы, рукав, дюймы, талия, дюймы, шея, сантиметры, грудь, сантиметры, Рукав, сантиметры, Талия, сантиметры, Длина стопы, мм, Длина стопы, дюймы, США, Канада, Великобритания, Австралия, Европа, континентальный, Япония, Россия, Франция, Италия, Испания, Китай, Корея, Мексика… МеханикаПреобразователь угловой скорости и частоты вращения : радиан / секунда, радиан / день, радиан / час, радиан / минута, градус / день, градус / час, градус / минута, градус / секунда, оборот / день, оборот / час, оборот / минута, оборот / секунда, оборот / год, оборот / месяц, оборот / неделя, градус / год, градус / месяц, градус / неделя, радиан / год, радиан / месяц, радиан / неделя. Преобразователь ускорения : дециметр / секунда², метр / секунда², километр / секунда², гектометр / секунда², декаметр / секунда², сантиметр / секунда², миллиметр / секунда², микрометр / секунда², нанометр / секунда², пикометр / секунда², фемтометр / секунда² , аттометр / секунда², галлон, галилей, миля / секунда², ярд / секунда², фут / секунда², дюйм / секунда², ускорение свободного падения, ускорение свободного падения на Солнце, ускорение свободного падения на Меркурии, ускорение свободного падения на Венере , ускорение свободного падения на Луне, ускорение свободного падения на Марсе, ускорение свободного падения на Юпитере, ускорение свободного падения на Сатурне… Конвертер плотности : килограмм / метр³, килограмм / сантиметр³, грамм / метр³, грамм / сантиметр³, грамм / миллиметр³, миллиграмм / метр³, миллиграмм / сантиметр³, миллиграмм / миллиметр³, экзаграмм / литр, петаграмм / литр, тераграмм / литр, гигаграмм / литр, мегаграмм / литр, килограмм / литр, гектограмм / литр, декаграмм / литр, грамм / литр, дециграмм / литр, сантиграмм / литр, миллиграмм / литр, микрограмм / литр, нанограмм / литр, пикограмм / литр , фемтограмм / литр, аттограмм / литр, фунт / дюйм³ … Конвертер удельного объема : метр³ / килограмм, сантиметр³ / грамм, литр / килограмм, литр / грамм, фут³ / килограмм, фут³ / фунт, галлон (США ) / фунт, галлон (Великобритания) / фунт. Преобразователь момента инерции : килограмм-метр², килограмм-сантиметр², килограмм-миллиметр², грамм-сантиметр², грамм-миллиметр², килограмм-сила-метр-секунда², унция-дюйм², унция-сила-дюйм-секунда², фунт-фут², фунт-сила-фут-секунда, фунт²-дюйм , фунт-сила-дюйм-секунда², ударный фут². Конвертер момента силы : метр ньютон, метр килоньютон, метр миллиньютон, метр микроньютон, метр тонна-сила (короткий), метр тонна-сила (длинный), метр тонна-сила (метрический), метр килограмм-сила, грамм-сила-сантиметр, фунт-сила-фут, фунт-фут, фунт-дюйм. Гидротрансформатор : ньютон-метр, ньютон-сантиметр, ньютон-миллиметр, килоньютон-метр, дин-сантиметр, дин-миллиметр, килограмм-сила-метр, килограмм-сила-сантиметр, килограмм-сила-миллиметр, грамм-сила-метр, грамм- сила-сантиметр, грамм-сила-миллиметр, унция-сила-фут, унция-сила-дюйм, фунт-сила-фут, фунт-сила-дюйм. Термодинамика — теплоКонвертер удельной энергии, теплоты сгорания (на массу) : джоуль / килограмм, килоджоуль / килограмм, калория (IT) / грамм, калория (th) / грамм, BTU (IT) / фунт, BTU (th) / фунт, килограмм / джоуль, килограмм / килоджоуль, грамм / калория (IT), грамм / калория (th), фунт / BTU (IT), фунт / Btu (th), фунт / лошадиная сила-час, грамм / лошадиная сила (метрическая) -час, грамм / киловатт-час. Конвертер удельной энергии, теплоты сгорания (на объем) : джоуль / метр³, джоуль / литр, мегаджоуль / метр³, килоджоуль / метр³, килокалория (IT) / метр³, калория (IT) / сантиметр³, терм / фут³, терм / галлон (Великобритания), британские тепловые единицы (IT) на фут³, британские тепловые единицы на фут³, CHU / фут³, метр³ / джоуль, литр / джоуль, галлон (США) / лошадиная сила-час, галлон (США) / лошадиная сила (метрическая система) )-час. Конвертер теплопроводности : ватт / метр / K, ватт / сантиметр / ° C, киловатт / метр / K, калория (IT) / секунда / сантиметр / ° C, калория (th) / секунда / сантиметр / ° C , килокалория (IT) / час / метр / ° C, килокалория (th) / час / метр / ° C, BTU (IT) дюйм / секунда / фут² / ° F, BTU (th) дюйм / секунда / фут² / ° F , Btu (IT) фут / час / фут² / ° F, Btu (th) фут / час / фут² / ° F, BTU (IT) дюйм / час / фут² / ° F, BTU (th) дюйм / час / фут² / ° F. Конвертер удельной теплоемкости : джоуль / килограмм / K, джоуль / килограмм / ° C, джоуль / грамм / ° C, килоджоуль / килограмм / K, килоджоуль / килограмм / ° C, калория (IT) / грамм / ° C, калория (IT) / грамм / ° F, калория (th) / грамм / ° C, килокалория (IT) / килограмм / ° C, килокалория (th) / килограмм / ° C, килокалория (IT) / килограмм / K , килокалория (th) / килограмм / K, килограмм-сила-метр / килограмм / K, фунт-сила-фут / фунт / ° R, Btu (IT) / фунт / ° F, Btu (th) / фунт / ° F, Btu (IT) / фунт / ° R, Btu (th) / фунт / ° R, Btu (IT) / фунт / ° C, CHU / фунт / ° C. Конвертер плотности теплового потока : ватт / метр², киловатт / метр², ватт / сантиметр², ватт / дюйм², джоуль / секунда / метр², килокалория (IT) / час / метр², килокалория (IT) / час / фут², калория (IT) / минута / сантиметр², калория (IT) / час / сантиметр², калория (th) / минута / сантиметр², калория (th) / час / сантиметр², дина / час / сантиметр, эрг / час / миллиметр², фут-фунт / минута на фут², мощность в лошадиных силах на фут², мощность (метрическая) на фут², BTU (IT) / секунда на фут², BTU (IT) / минута на фут², Btu (IT) / час на фут², BTU (th) / секунда на дюйм² , Btu (th) / секунда / фут², Btu (th) / минута / фут², Btu (th) / час / фут², CHU / час / фут². Конвертер коэффициента теплопередачи : ватт / метр² / K, ватт / метр² / ° C, джоуль / секунда / метр² / K, килокалория (IT) / час / метр² / ° C, килокалория (IT) / час / фут² / ° C, BTU (IT) / секунда / фут² / ° F, Btu (th) / секунда / фут² / ° F, BTU (IT) / час / фут² / ° F, Btu (th) / час / фут² / ° F, CHU / час / фут² / ° C. Гидравлика — жидкостиКонвертер объемного расхода : метр³ / секунда, метр³ / день, метр³ / час, метр³ / минута, сантиметр³ / день, сантиметр³ / час, сантиметр³ / минуту, сантиметр³ / секунда, литр / день, литр / час, литр / минута, литр / секунда, миллилитр / день, миллилитр / час, миллилитр / минута, миллилитр / секунда, галлон (США) / день, галлон (США) / час, галлон (США) / минута, галлон (США) в секунду, галлон (Великобритания) в день, галлон (Великобритания) в час, галлон (Великобритания) в минуту, галлон (Великобритания) в секунду, килобаррель (США) в день, баррель (США) в день… Конвертер массового расхода : килограмм / секунда, грамм / секунда, грамм / минута, грамм / час, грамм / день, миллиграмм / минута, миллиграмм / час, миллиграмм / день, килограмм / минута, килограмм / час , килограмм / день, экзаграмм / секунда, петаграмма / секунда, тераграмма / секунда, гигаграмма / секунда, мегаграмм / секунда, гектограмм / секунда, декаграмма / секунда, дециграмма / секунда, сантиграмма / секунда, миллиграмм / секунда, микрограмм / секунда, тонна (метрическая) / секунда, тонна (метрическая) / минута, тонна (метрическая) / час, тонна (метрическая) / день … Конвертер молярной скорости потока : моль / секунда, экзамен / секунда, петамоль / секунда, терамоль в секунду, гигамоль в секунду, мегамоль в секунду, киломоль в секунду, гектомоль в секунду, декамоль в секунду, децимоль в секунду, сантимоль в секунду, миллимоль в секунду, микромоль в секунду, наномоль в секунду, пикомоль в секунду, фемтомоль в секунду. секунда, аттомоль в секунду, моль в минуту, моль в час, моль в день, миллимоль в минуту, миллимоль в час, миллимоль в день, километр в минуту, километр в час, километр в день. Mass Flux Converter : грамм / секунда / метр², килограмм / час / метр², килограмм / час / фут², килограмм / секунда / метр², грамм / секунда / сантиметр², фунт / час / фут², фунт / секунда / фут². Конвертер молярной концентрации : моль / метр³, моль / литр, моль / сантиметр³, моль / миллиметр³, километр / метр³, километр / литр, километр / сантиметр³, километр / миллиметр³, миллимоль / метр³, миллимоль / литр, миллимоль / сантиметр³, миллимоль / миллиметр³, моль / дециметр³, молярный, миллимолярный, микромолярный, наномолярный, пикомолярный, фемтомолярный, аттомолярный, зептомолярный, йоктомолярный. Массовая концентрация в конвертере раствора : килограмм / литр, грамм / литр, миллиграмм / литр, часть / миллион, гран / галлон (США), гран / галлон (Великобритания), фунт / галлон (США), фунт / галлон (Великобритания), фунт / миллион галлон (США), фунт / миллион галлон (Великобритания), фунт / фут³, килограмм / метр³, грамм / 100 мл. Конвертер динамической (абсолютной) вязкости : паскаль-секунда, килограмм-сила-секунда на метр², ньютон-секунда на метр², миллиньютон-секунда на метр², дин-секунда на сантиметр², равновесие, эксапуаз, петапуаз, терапуаз, гигапуаз, мегапуаз, килопуаз, гектопуаз, декапуаз, деципуаз, сантипуаз, миллипуаз, микропуаз, наноуаз, пикопуаз, фемтопуаз, аттопуаз, фунт-сила-секунда / дюйм², фунт-сила-секунда / фут², фунт-секунда / фут², грамм / сантиметр / секунда… Конвертер кинематической вязкости : метр² / секунда, метр² / час, сантиметр² / секунда, миллиметр² / секунда, фут² / секунда, фут² / час, дюйм² / секунда, стоксы, экзастоки, петастоксы, терастоки, гигастоксы, мегастоксы, килостоки, гектостоки, декастоки, децистоки, сантистоки, миллистоки, микростоки, наностоки, пикостоки, фемтостоки, аттостоки. Преобразователь поверхностного натяжения : ньютон на метр, миллиньютон на метр, грамм-сила на сантиметр, дина на сантиметр, эрг / сантиметр², эрг / миллиметр², фунт на дюйм, фунт-сила / дюйм. Акустика — ЗвукПреобразователь чувствительности микрофона : децибел относительно 1 вольт на 1 паскаль, децибел относительно 1 вольта на 1 микропаскаль, децибел относительно 1 вольта на 1 дин на квадратный сантиметр, децибел относительно 1 вольт на 1 микробар, вольт на паскаль, милливольт на паскаль, микровольт на паскаль. Преобразователь уровня звукового давления (SPL) : ньютон на квадратный метр, паскаль, миллипаскаль, микропаскаль, дин / квадратный сантиметр, бар, миллибар, микробар, уровень звукового давления в децибелах. Фотометрия — светКонвертер яркости : кандела на метр², кандела на сантиметр², кандела на фут², кандела на дюйм², килокандела на метр², стильб, люмен на метр² / стерадиан, люмен на сантиметр² / стерадиан² / люмен стерадиан, нит, миллинит, ламберт, миллиламберт, фут-ламберт, апостиль, блондель, брил, скот. Конвертер силы света : кандела, свеча (немецкий язык), свеча (Великобритания), десятичная свеча, свеча (пентан), пентановая свеча (мощность 10 свечей), свеча Хефнера, единица измерения яркости, десятичный буж, люмен / стерадиан, свеча (Международный). Конвертер освещенности : люкс, метр-свеча, сантиметр-свеча, фут-свеча, фот, nox, кандела стерадиан на метр², люмен на метр², люмен на сантиметр², люмен на фут², ватт на сантиметр² (при 555 нм) . Преобразователь частоты и длины волны : герцы, эксагерцы, петагерцы, терагерцы, гигагерцы, мегагерцы, килогерцы, гектогерцы, декагерцы, децигерцы, сантигерцы, единицы длины волны, микрогерцы, микрогерцы, микрогерцы, миллигерцы, миллигерцы, секунды , длина волны в петаметрах, длина волны в тераметрах, длина волны в гигаметрах, длина волны в мегаметрах, длина волны в километрах, длина волны в гектометрах, длина волны в декаметрах… Конвертер оптической силы (диоптрии) в фокусное расстояние : Оптическая сила (диоптрическая сила или преломляющая сила) линзы или другой оптической системы — это степень, с которой система сходится или рассеивает свет. Он рассчитывается как величина, обратная фокусному расстоянию оптической системы и измеряется в инверсных метрах в СИ или, чаще, в диоптриях (1 диоптрия = м⁻¹) ЭлектротехникаКонвертер электрического заряда : кулон, мегакулон , килокулон, милликулон, микрокулон, нанокулон, пикокулон, абкулон, EMU заряда, статкулон, ESU заряда, франклин, ампер-час, миллиампер-час, ампер-минута, ампер-секунда, фарадей (на основе углерода 12), элементарный плата. Преобразователь электрического тока : ампер, килоампер, миллиампер, биот, абампер, ЭДС тока, статампер, ЭДС тока, СГС э.м. единица, CGS e.s. единица, микроампер, наноампер, ток Планка. Линейный преобразователь плотности тока : ампер / метр, ампер / сантиметр, ампер / дюйм, абампер / метр, абампер / сантиметр, абампер / дюйм, эрстед, гильберт / сантиметр, ампер / миллиметр, миллиампер / метр, миллиампер , миллиампер / сантиметр, миллиампер / миллиметр, микроампер / метр, микроампер / дециметр, микроампер / сантиметр, микроампер / миллиметр. Преобразователь поверхностной плотности тока : ампер / метр², ампер / сантиметр², ампер / дюйм², ампер / мил², ампер / круговой мил, абампер / сантиметр², ампер / миллиметр², миллиампер / миллиметр², микроампер / миллиметр², миллиампер / миллиметр², миллиампер / миллиметр² миллиампер / сантиметр², микроампер / сантиметр², килоампер / сантиметр², ампер / дециметр², миллиампер / дециметр², микроампер / дециметр², килоампер / дециметр². Преобразователь напряженности электрического поля : вольт на метр, киловольт на метр, киловольт на сантиметр, вольт на сантиметр, милливольт на метр, микровольт на метр, киловольт на дюйм, вольт на дюйм, вольт на мил, абвольт на сантиметр, статвольт / сантиметр, статвольт / дюйм, ньютон / кулон, вольт / микрон. Преобразователь электрического потенциала и напряжения : вольт, милливольт, микровольт, нановольт, пиковольт, киловольт, мегавольт, гигавольт, теравольт, ватт / ампер, абвольт, EMU электрического потенциала, статвольт, ESU электрического потенциала, планковский электрический потенциал. Преобразователь электрического сопротивления : Ом, мегаом, микром, вольт / ампер, обратный сименс, абом, EMU сопротивления, статом, ESU сопротивления, квантованное сопротивление Холла, импеданс Планка, миллиом, кОм. Преобразователь удельного электрического сопротивления : омметр, ом-сантиметр, ом-дюйм, микром-сантиметр, микром-дюйм, ом-сантиметр, статом-сантиметр, круговой мил-ом / фут, ом-кв.миллиметр на метр. Преобразователь электрической проводимости : сименс, мегасименс, килосименс, миллисименс, микросименс, ампер / вольт, mho, gemmho, micromho, abmho, statmho, квантованная проводимость Холла. Конвертер электропроводности : сименс / метр, пикосименс / метр, mho / метр, mho / сантиметр, abmho / метр, abmho / сантиметр, статмо / метр, статмо / сантиметр, сименс / сантиметр, миллисименс / метр, миллисименс / сантиметр, микросименс / метр, микросименс / сантиметр, единица электропроводности, коэффициент проводимости, доли на миллион, шкала 700, шкала частей на миллион, шкала 500, частей на миллион, шкала 640, TDS, частей на миллион, шкала 640, TDS, части на миллион, шкала 550, TDS, частей на миллион, шкала 500, TDS, частей на миллион, шкала 700. Преобразователь емкости : фарад, экзафарад, петафарад, терафарад, гигафарад, мегафарад, килофарад, гектофарад, декафарад, децифарад, сентифарад, миллифарад, микрофарад, емкость, нанофарад, аттофарад, ед. , статфарад, ЭСУ емкости. Преобразователь индуктивности : генри, эксагенри, петагенри, терагенри, гигагенри, мегагенри, килогенри, гектогенри, декагенри, децигенри, сантигенри, миллигенри, микрогенри, наногенри, пикогенри, аттогенри, энтогенри, энтогенри, энтогенри , статенри, ЭСУ индуктивности. Преобразователь реактивной мощности переменного тока : реактивный вольт-ампер, реактивный милливольт-ампер, реактивный киловольт-ампер, реактивный мегавольт-ампер, реактивный гигавольт-ампер. Американский калибр проводов : Американский калибр проводов (AWG) — это стандартизированная система калибра проводов, используемая в Соединенных Штатах и Канаде для измерения диаметров цветных электропроводящих проводов, включая медь и алюминий. Чем больше площадь поперечного сечения провода, тем выше его допустимая нагрузка по току.Чем больше номер AWG, также называемый калибром провода, тем меньше физический размер провода. Самый большой размер AWG — 0000 (4/0), а самый маленький — 40. В этой таблице перечислены размеры и сопротивление AWG для медных проводников. Используйте закон Ома для расчета падения напряжения на проводнике. Магнитостатика, магнетизм и электромагнетизмПреобразователь магнитного потока : Вебер, милливебер, микровебер, вольт-секунда, единичный полюс, мегалин, килолин, линия, максвелл, тесла-метр², тесла-сантиметр², гаусс-сантиметр², квант магнитного потока. Преобразователь плотности магнитного потока : тесла, Вебер / метр², Вебер / сантиметр², Вебер / дюйм², Максвелл / метр², Максвелл / сантиметр², Максвелл / дюйм², Гаусс, линия / сантиметр², линия / дюйм², гамма. Radiation and RadiologyКонвертер мощности поглощенной дозы излучения, суммарной мощности дозы ионизирующего излучения : серый цвет в секунду, эксагрей в секунду, петагрей в секунду, тераграрей в секунду, гигаграй в секунду, мегагрей в секунду, килограмм в секунду, гектоград. / секунда, декаграй / секунда, дециграй / секунда, сантигрей / секунда, миллиграй / секунда, микрогрей / секунда, наногрей / секунда, пикграй / секунда, фемтогрей / секунда, аттогрей / секунда, рад / секунда, джоуль / килограмм / секунда, ватт на килограмм, зиверт в секунду, миллизиверт в год, миллизиверт в час, микрозиверт в час, бэр в секунду, рентген в час… Радиоактивность. Конвертер радиоактивного распада : беккерель, петабеккерель, терабеккерель, гигабеккерель, мегабеккерель, килобеккерель, миллибеккерель, кюри, килокюри, милликюри, микрокюри, нанокюри, пикокюри, резерфорд, одно / секунда, дезинтеграция. Конвертер облучения : кулон на килограмм, милликулон на килограмм, микрокулон на килограмм, рентген, миллирентген, микрорентген, тканевый рентген, Паркер, респ. Радиация. Конвертер поглощенной дозы : рад, миллирад, джоуль / килограмм, джоуль / грамм, джоуль / сантиграм, джоуль / миллиграмм, серый, эксагрей, петагрей, терагрей, гигагрей, мегагрей, килограмм, гектагрей, декагрей, декаграй, сантигрей, микрогрей, миллиграм , наногрей, пикограй, фемтогрей, аттогрей, зиверт, миллизиверт, микрозиверт … Прочие преобразователиКонвертер метрических префиксов : нет, yotta, zetta, exa, peta, tera, giga, mega, kilo, hecto, deka , деци, санти, милли, микро, нано, пико, фемто, атто, зепто, йокто. Преобразователь передачи данных : бит / секунда, байт / секунда, килобит / секунда (SI по умолчанию), килобайт / секунда (SI по умолчанию), кибибит / секунда, кибибайт / секунда, мегабит / секунда (SI по умолчанию) , мегабайт в секунду (SI по умолчанию), мебибит в секунду, мебибайт в секунду, гигабит в секунду (SI по умолчанию), гигабайт в секунду (SI по умолчанию), гибибит в секунду, гибибит в секунду, терабит в секунду (SI по умолчанию). .), терабайт в секунду (по умолчанию SI), тебибит в секунду, тебибайт в секунду, Ethernet, Ethernet (быстрый), Ethernet (гигабит), OC1, OC3, OC12, OC24, OC48 … Типографика и цифровой Конвертер единиц изображения : твип, метр, сантиметр, миллиметр, символ (X), символ (Y), пиксель (X), пиксель (Y), дюйм, пика (компьютер), пика (принтер), точка (DTP / PostScript) ), point (компьютер), point (принтер), en, cicero, em, Didot point. Конвертер единиц измерения объема пиломатериалов : кубический метр, кубический фут, кубический дюйм, футы для досок, тысяча футов для досок, шнур, шнур (80 фут³), футы для шнура, узел, поддон, поперечина, стяжка переключателя. Калькулятор молярной массы : Молярная масса — это физическое свойство, которое определяется как масса вещества, деленная на количество вещества в молях. Другими словами, это масса одного моля определенного вещества. Периодическая таблица : Периодическая таблица представляет собой список всех химических элементов, упорядоченных слева направо и сверху вниз по их атомным номерам, электронным конфигурациям и повторяющимся химическим свойствам, расположенным в форме таблицы таким образом, чтобы элементы с аналогичные химические свойства отображаются в вертикальных столбцах, называемых группами.У некоторых групп есть имена, а также номера. Например, все элементы группы 1, кроме водорода, являются щелочными металлами, а элементы группы 18 — благородными газами, которые ранее назывались инертными газами. Различные строки таблицы называются периодами, потому что это расположение отражает периодическое повторение сходных химических и физических свойств химических элементов по мере увеличения их атомного номера. Элементы одного периода имеют одинаковое количество электронных оболочек. У вас есть трудности с переводом единицы измерения на другой язык? Помощь доступна! Задайте свой вопрос в TCTerms , и вы получите ответ от опытных технических переводчиков в считанные минуты. |
Упрощенный тормозной путь | RAC Drive
При скорости 20 миль в час тормозной путь точно такой же, как и расстояние мыслей. В совокупности они обеспечивают общий тормозной путь 12 метров.
При скорости 70 миль в час 75-метровый тормозной путь составляет почти 80% от общего 96-метрового тормозного пути.
Приемы запоминания тормозного пути
Тормозной путь — любимая часть теоретического теста, но запомнить его нелегко.Это если вы не знаете особого трюка… который мы здесь раскроем.
Это требует немного математики, но терпите. Все, что вам нужно сделать, это умножить скорость на 0,5, начиная с 2. Это даст вам тормозной путь в футах, который является приемлемым для теоретического теста. Например…
20 миль в час x 2 = 40 футов
30 миль в час x 2,5 = 75 футов
40 миль в час x 3 = 120 футов
50 миль в час x 3,5 = 175 футов
60 миль в час x 4 = 240 футов
70 миль в час x 4,5 = 315 футов
Их 3.3 фута в метре — разделите расстояние в футах на 3,3, чтобы получить тормозной путь в метрах. Для этого вам понадобится калькулятор, но он не нужен для проверки теории.
Какие еще факторы влияют на тормозной путь?
Как мы уже упоминали, тормозной путь может зависеть от ряда факторов.
Некоторые люди предполагают, что тормозной путь в Правилах дорожного движения устарел, потому что современные автомобили с системами ABS и лучшими шинами могут останавливаться намного быстрее.
Но помните, что такие факторы влияют только на тормозной путь. Если автомобиль не оборудован системой автоматического экстренного торможения, это не сократит время обдумывания.
1. Погода
В плохих погодных условиях общий тормозной путь автомобиля может быть больше по ряду причин. Во-первых, плохая видимость может означать, что водителю требуется больше времени, чтобы отреагировать, увеличивая его / ее дистанцию мышления. Но на скользкой дороге, вызванной дождем, снегом или льдом, тормозной путь также увеличивается.
Исследования показывают, что тормозной путь можно увеличить вдвое на мокрой дороге и в 10 раз на снегу или льду. Это означает, что в снегу вам может понадобиться преодолеть расстояние, превышающее семь футбольных полей, чтобы остановиться со скоростью 70 миль в час.
Чтобы справиться с погодными условиями, ознакомьтесь с нашим руководством по зимнему вождению.
2. Состояние дороги
Это не всегда так очевидно, ведь «плохая погода означает большой тормозной путь». Дорога может быть особенно жирной, если после жаркой погоды прошел дождь или на нее пролили масло.
Будьте готовы к гололеду в холодные дни и следите за рыхлыми поверхностями, такими как гравий. Все это может затруднить поспешную остановку.
ПОДРОБНЕЕ: Как управлять автоматической коробкой передач
3. Состояние водителя
Хотя все эти факторы могут повлиять на тормозной путь, человек за рулем отвечает за расстояние мышления — и это может иметь огромное влияние на общий тормозной путь.
Возраст водителя, степень его бодрствования и употребление наркотиков или алкоголя могут повлиять на то, как быстро он отреагирует.
Использование мобильного телефона вместо того, чтобы сосредоточиться на дороге, может иметь разрушительные последствия для тормозного пути водителя — всего несколько секунд, взглянув на свой телефон, можно добавить футбольное поле к общему тормозному пути на скоростях автострады. Если впереди движение остановилось, это может очень быстро испортить вам день.
Другие отвлекающие факторы в машине, такие как громкая музыка и пассажиры, также могут повлиять на время обдумывания перед тем, как нажать на тормоз.
4. Состояние автомобиля
Хотя многие современные автомобили действительно могут останавливаться на более коротких дистанциях, чем указано в официальных Правилах дорожного движения, состояние автомобиля также может иметь значение.
Например, автомобилям с бюджетными шинами может потребоваться дополнительно 14 метров для остановки на скорости 70 миль в час на мокрой дороге по сравнению с автомобилями с шинами премиум-класса или пять метров на сухой дороге.
Исследования также показали, что для шин с допустимым пределом протектора 1,6 мм может потребоваться на 60% больше дороги для остановки по сравнению с совершенно новыми шинами.
Недокачанные шины также влияют на тормозной путь, как и автомобили с плохо обслуживаемыми тормозами.
Щелкните здесь, чтобы узнать больше о важности состояния шин и посмотреть видео о том, как проверить состояние шин.
Проверьте тормозные колодки, чтобы убедиться, что в них осталось достаточно жизни, и проверьте тормоза после проезда по воде, чтобы проверить, не осталось ли влаги между колодками и дисками.
Подробнее о тормозных колодках читайте в нашем подробном руководстве по уходу за тормозными колодками.
Для полного спокойствия дома и на дороге приобретите RAC Breakdown Cover сегодня.
Вернитесь в раздел нашего ученика-водителя
Видео с вопросом: Расчет тормозного пути с учетом времени реакции, скорости автомобиля и замедления
Стенограмма видео
Время реакции водителя автомобиля, движущегося со скоростью 20 метров в секунду, равно 1.2 секунды. Тормоза автомобиля замедляют автомобиль со скоростью 4,5 метра в секунду в квадрате после активации. Какой тормозной путь с точностью до метра?
Хорошо, в этом вопросе мы рассматриваем автомобиль, который изначально движется. А потом это прекратится. Допустим, эта оранжевая рамка представляет нашу машину. Нам сказали, что эта машина изначально движется со скоростью 20 метров в секунду. Итак, давайте произвольно выберем, что изначально машина двигалась вправо со скоростью 20 метров в секунду.Это начальная скорость автомобиля, которую мы назовем. Теперь с этой машиной происходит то, что она изначально движется со скоростью 20 метров в секунду. И тогда водитель замечает опасность.
Итак, допустим, это опасность, которую замечает водитель. Это огромный валун на пути машины. Теперь давайте также предположим, что водитель замечает опасность, когда автомобиль находится здесь в этом положении. И с этого момента драйвер начинает обработку, которую ему нужно сломать. Однако, поскольку у водителя время реакции равно 1.2 секунды они не сразу нажимают на тормоза. Другими словами, автомобиль все еще движется со скоростью 20 метров в секунду на небольшом расстоянии до того, как водитель нажмет на тормоз.
Таким образом, на всем протяжении этого расстояния водитель вместе с автомобилем продолжали двигаться со скоростью 20 метров в секунду, в то время как водитель думает о нажатии на тормоз. Теперь это конкретное расстояние известно как расстояние мышления, которое мы будем называть 𝑑 нижним индексом. Но затем, как только машина достигает этой точки, водитель нажимает на тормоза.И именно в этот момент машина начинает замедляться. Другими словами, с этого момента автомобиль теперь ускоряется в направлении, противоположном его первоначальному движению, со скоростью 4,5 метра в секунду в квадрате.
Итак, именно в этот момент мы видим, что ускорение, которое автомобиль испытывает при торможении, имеет направление, противоположное его начальной скорости. И это, конечно, потому, что машина замедляется. Но поскольку мы имеем дело со скоростью автомобиля, изначально движущейся в направлении, противоположном ускорению, было бы неплохо выбрать условные обозначения.Давайте выберем, что все, что направо, движется в положительном направлении. И все, что находится слева, движется в отрицательном направлении. Другими словами, тогда начальная скорость автомобиля, которая двигалась вправо, положительна 20 метров в секунду, тогда как ускорение или, скорее, замедление автомобиля, которое движется влево, будет обозначено отрицательными 4,5 метра в секунду. в наших расчетах.
А теперь назовем ускорение автомобиля 𝑎. И затем, как только в этот момент автомобиль начинает замедляться, мы знаем, что в конечном итоге автомобиль остановится, надеюсь, прежде чем он достигнет опасности.Итак, в этот момент автомобиль остановился, что означает, что конечная скорость автомобиля, которую мы назовем 𝑣, равна нулю метров в секунду, потому что теперь автомобиль неподвижен. Таким образом, расстояние, которое автомобиль проходит за период времени, когда он замедляется, называется тормозным путем, который мы назовем 𝑑 нижним индексом.
Тормозной путь называется потому, что это расстояние, на котором были задействованы тормоза автомобиля. И, кстати, мы также должны отметить, что в начале тормозного пути скорость автомобиля все еще составляла 20 метров в секунду.Теперь нас просят найти тормозной путь автомобиля. Итак, давайте вспомним, что тормозной путь автомобиля определяется как расстояние мысли плюс тормозной путь. Итак, допустим, что тормозной путь автомобиля мы будем называть 𝑑 индексом. И, как мы уже видели, дистанция мышления — это 𝑑 нижний индекс. И тормозной путь — индекс.
Другими словами, тормозной путь здесь — это общее расстояние. Это расстояние, которое проехала машина между моментом, когда водитель впервые осознает, что впереди есть опасность, и моментом, когда машина наконец останавливается.Итак, давайте запишем здесь, что тормозной путь равен расстоянию мысли плюс тормозной путь. И давайте по отдельности определим дистанцию мышления и тормозной путь.
Начнем с дистанции мышления. Теперь, когда автомобиль движется от точки, в которой водитель понимает, что им нужно остановиться, до точки, когда водитель действительно нажимает на тормоза, как мы уже говорили ранее, машина продолжает двигаться со скоростью 20 метров в секунду, потому что тормоза не работают. еще не нажали.Другими словами, автомобиль движется с постоянной скоростью 𝑢 на всем протяжении этого расстояния. Затем мы можем вспомнить, что если объект движется с постоянной скоростью, назовем эту скорость 𝑣 индексом const, тогда эта скорость равна расстоянию, пройденному объектом, деленному на время, затраченное на то, чтобы этот объект прошел это расстояние. Итак, в нашем частном случае машина движется с постоянной скоростью. И эта постоянная скорость равна пройденному расстоянию, так что это мысленное расстояние, деленное на время, необходимое автомобилю, чтобы проехать это расстояние.
Теперь, как мы знаем, автомобиль на самом деле преодолевает это расстояние за 1,2 секунды, потому что это время реакции водителя, другими словами, время, которое проходит между этим моментом, когда водитель понимает, что ему нужно затормозить, и здесь , когда они действительно нажимают на тормоз. Итак, мы знаем значение, 20 метров в секунду. И мы знаем значение 𝑡, время реакции, 1,2 секунды. Таким образом, мы можем изменить это уравнение, чтобы найти 𝑑 𝑡. Мы делаем это, умножая обе части уравнения на время реакции.Таким образом, он отменяется с правой стороны. И что у нас осталось, так это то, что время реакции водителя, умноженное на постоянную скорость, с которой движется автомобиль, равно расстоянию, на которое можно подумать.
Тогда мы можем сказать, что расстояние мышления равно времени реакции, 1,2 секунды, умноженному на скорость автомобиля, 20 метров в секунду. Быстро подумав об единицах измерения, мы увидим, что в числителе указаны секунды. А затем у нас есть секунды, что означает, что единицы секунд будут отменены.И у нас останутся единицы измерения. Теперь это имеет смысл, потому что мы вычисляем расстояние для размышлений. Таким образом, оценивая правую часть этого уравнения, мы обнаруживаем, что расстояние мыслей машины составляет 24 метра.
Итак, давайте запишем эту информацию здесь. Мы только что выяснили, что такое 𝑑 𝑡. Итак, чтобы вычислить 𝑠, все, что нам теперь нужно сделать, это вычислить значение 𝑑 𝑏, тормозного пути. Для этого нам нужно понять, что на этой фазе движения машина больше не движется с постоянной скоростью.Фактически, он замедляется с постоянной скоростью 4,5 метра в секунду в квадрате или, если хотите, ускоряется с отрицательной скоростью 4,5 метра в секунду в квадрате.
Итак, что мы знаем об этой фазе движения автомобиля, так это то, что начальная скорость составляет 20 метров в секунду. И эта скорость положительна, потому что она направлена вправо. Мы также знаем, что конечная скорость автомобиля здесь — ноль метров в секунду. И мы также знаем ускорение автомобиля, отрицательное 4,5 метра в секунду в квадрате, потому что помните, что ускорение идет влево, другими словами, против движения самого автомобиля.Итак, если мы знаем эти три величины,, 𝑣 и 𝑎, и пытаемся определить тормозной путь 𝑑 𝑏, то для этого нам нужно вспомнить одно из кинематических уравнений.
Конкретное уравнение, которое мы ищем, — это уравнение, которое говорит нам, что квадрат конечной скорости равен квадрату начальной скорости плюс два, умноженных на ускорение объекта, умноженное на пройденное расстояние. прямая линия по объекту. Но в этой ситуации расстояние, пройденное объектом по прямой линии, которым в данном случае является автомобиль, на самом деле является тормозным путем.Следовательно, мы можем заменить 𝑑 𝑠 в уравнении на 𝑑 𝑏, тормозной путь.
Мы можем оставить все остальные величины такими же, потому что мы назвали их 𝑢, 𝑣 и 𝑎. И, конечно же, они означают одно и то же. Итак, на этом этапе мы можем взять наше уравнение и перестроить его, чтобы найти 𝑑 𝑏. Если мы начнем с вычитания в квадрате из обеих частей уравнения, то у нас останется 𝑣 в квадрате минус 𝑢 в квадрате с одной стороны и только два 𝑎𝑑 𝑏 справа. Затем мы разделим обе части уравнения на два, чтобы получить в квадрате минус 𝑢 в квадрате, разделенном на два 𝑎 слева и просто 𝑑 𝑏 справа.Итак, теперь все, что нам нужно сделать, это ввести некоторые значения.
Когда мы это делаем, мы получаем в квадрате минус 𝑢 в квадрате, разделенном на два. Затем мы можем упростить числитель, который становится отрицательным 400 метров в квадрате на секунду в квадрате, когда мы не забываем возвести в квадрат все в скобках из предыдущего, и знаменатель становится равным двум, умноженным на отрицательные 4,5 метра в секунду в квадрате, что становится отрицательными девятью метрами. на секунду в квадрате. А затем в этот момент мы видим, что отрицательный знак числителя и знаменателя отменяется, поэтому для нас было так важно учесть направление ускорения автомобиля.А если мы подумаем о единицах измерения, то увидим, что у нас есть квадрат в квадрате на секунду в числителе и в метрах на секунду в квадрате в знаменателе.
У нас такая же степень секунды. И они собираются отменить. Но в числителе у нас есть метры в квадрате, тогда как в числителе у нас просто метры. Таким образом, только одна степень счетчика в числителе сократится с единицей степени счетчика в знаменателе. И окончательный результат будет в метрах, и это здорово, потому что мы снова находим расстояние.Таким образом, наше расстояние будет 400 разделенных на девять метров. Когда мы оцениваем это, мы обнаруживаем, что оно становится равным 44,44 и т. Д. Метра.
Итак, давайте запишем эту информацию здесь. 𝑑 𝑏 равно 44,4 повторяющимся метрам. И в этот момент мы понимаем, что почти у цели. Мы видим, что 𝑑 𝑠, тормозной путь, который мы пытаемся вычислить, равен расстоянию мысли плюс тормозной путь. Итак, можно сказать, что тормозной путь равен 24 метрам плюс 44.4 повторяющихся метра. В итоге получается 68,4 повторяющихся метра. Однако мы еще не пришли к окончательному ответу на наш вопрос.
Помните, нас просили найти тормозной путь автомобиля с точностью до метра. Итак, нам нужно округлить 68,4 метра до ближайшего метра. Для этого нам нужно посмотреть на это значение после десятичной точки. Это значение четыре, что меньше пяти. И, следовательно, это значение, восьмерка, останется прежним. Не собираюсь облавливать.И вот мы пришли к ответу на наш вопрос. Тормозной путь этой машины составляет 68 метров с точностью до метра.
Как рассчитать тормозной путь? — Mvorganizing.org
Как рассчитать тормозной путь?
Формула для расчета тормозного пути. Следующая формула оказалась полезной для расчета тормозного пути: (Скорость ÷ 10) × (Скорость ÷ 10). Таким образом, на скорости 100 км / ч тормозной путь составляет 100 метров..
Сколько футов вам потребуется, чтобы остановиться на скорости 60 миль в час?
140 футов
Сколько футов нужно, чтобы остановиться на скорости 20 миль в час?
Средний тормозной путь Средний автомобиль, движущийся со скоростью 20 миль в час, проедет 20 футов до полной остановки, однако автомобилю, движущемуся со скоростью 40 миль в час, потребуется 80 футов, чтобы остановиться — вот почему так важно не превышать ограничение скорости. .
Что такое тормозной путь автомобиля?
Тормозной путь — это расстояние, которое транспортное средство будет преодолевать от точки, когда его тормоза полностью задействованы, когда дело доходит до полной остановки.Другой компонент — это расстояние реакции, которое является произведением скорости и времени восприятия-реакции водителя / гонщика.
Увеличивает ли тормозной путь скорость?
Тормозной путь автомобиля меняется в зависимости от скорости. Существует прямая зависимость от скорости: когда ваш автомобиль фактически полностью остановится, как только вы нажмете на тормоз. Время, необходимое автомобилю для остановки после нажатия на тормоз, является фактическим тормозным путем, и оно изменяется с каждым увеличением скорости.
Что может повлиять на тормозной путь?
На тормозной путь транспортного средства могут влиять:
- плохие дорожные и погодные условия, например мокрые или обледенелые дороги.
- плохое состояние автомобиля, например, изношенные тормоза или изношенные шины.
- большая скорость.
- масса автомобиля — чем больше масса, тем больше тормозной путь.
Тормозной путь прямо пропорционален скорости?
В отличие от дистанции мышления, тормозной путь не прямо пропорционален скорости. Небольшое увеличение скорости значительно увеличивает тормозной путь. Увеличение вдвое с 30 до 60 миль в час дает тот же эффект: торможение увеличивается в 4 раза с 14 до 56 м.
Расстояние зависит от скорости?
Как скорость влияет на расстояние остановки? Чем быстрее движется объект, тем большее расстояние требуется, чтобы остановиться. Если скорость автомобиля увеличивается вдвое, ему нужно примерно в 4 раза больше расстояния, чтобы остановиться. Если скорость автомобиля увеличивается втрое, ему нужно в 9 раз больше расстояния, чтобы остановиться.
Что происходит с тормозным путем при удвоении скорости?
Тормозное усилие — выше Тормозной путь увеличивается в четыре раза каждый раз, когда стартовая скорость удваивается.Это связано с тем, что работа, выполняемая по приведению автомобиля в состояние покоя, означает удаление всей его кинетической энергии. Таким образом, при фиксированной максимальной тормозной силе тормозной путь пропорционален квадрату скорости.
Скорость зависит от массы?
Масса не влияет на скорость напрямую. Он определяет, насколько быстро объект может изменять скорость (ускоряться) под действием заданной силы. Более легким объектам требуется меньше времени, чтобы изменить скорость на заданную величину под действием заданной силы.
Какая связь между скоростью и тормозным путем?
Тормозной путь пропорционален квадрату скорости автомобиля.Это математическое соотношение между начальной скоростью и тормозным путем показано на анимации ниже. Три автомобиля с одинаковыми тормозными системами движутся на трех разных скоростях.
Какие 5 факторов влияют на тормозной путь?
5 факторов, влияющих на тормозной путь
- Тяга. Сцепление — это мера способности шины воздействовать на поверхность дороги, изменяя движение грузовика — направление и / или скорость.
- Кривые.Когда грузовик поворачивается, часть тягового усилия его шин идет на изменение направления грузовика.
- Видимость.
- Трафик.
- Холмы.
Сколько времени нужно, чтобы останавливаться на мокрой дороге?
В общем, мокрые дороги могут удвоить тормозной путь. Чтобы остановить автомобиль на мокрой дороге, используя такой же тормозной путь, как и на сухой дороге, вам необходимо ехать медленнее. На мокрой дороге следует снизить скорость примерно на треть. Например, снизьте скорость с 65 миль в час до примерно 43 миль в час.
Увеличивает ли усталость тормозной путь?
Расстояние мышления зависит от времени реакции водителя, на которое могут повлиять наркотики, алкоголь, отвлекающие факторы и усталость. Более высокая скорость увеличивает как мыслительный, так и тормозной путь, увеличивая общий тормозной путь.
Влияет ли вес на тормозной путь?
Вес автомобиля абсолютно не влияет на тормозной путь. Большинство тяжелых автомобилей имеют более надежные тормозные системы, чем более легкие, поэтому их тормозной путь может быть даже короче, чем у легких.
Почему удвоение скорости увеличивает тормозной путь больше, чем удвоение массы?
Тормозной путь автомобиля увеличивается с увеличением массы. удвоение массы изменяет тормозной путь автомобиля. Тормоза автомобиля прилагают такое же усилие в 1500Н. Если автомобиль имеет удвоенную массу при 1500 кг, каково его ускорение?
Почему тормозной путь увеличивается с увеличением массы?
Вот где появляется масса: более тяжелые машины сильнее толкают дорогу.Это увеличивает трение. Таким образом, автомобили с большей массой имеют большее трение о землю, что уменьшает тормозной путь. Вывод: автомобили с большей массой имеют больший импульс, что увеличивает тормозной путь.
Зависит ли тормозной путь от массы?
Итак, масса не влияет на тормозной путь в очень простой модели, такой как два блока разной массы. Однако в случае грузовика и легкового автомобиля трение о землю составляет лишь небольшую часть тормозной силы.Большая часть этого обеспечивается сопротивлением воздуха, трением внутри системы и т. Д.
Каково расстояние мыслей для транспортного средства, движущегося со скоростью 20 миль в час?
Тормозной путь при разной скорости
| Скорость | Мышление + тормозной путь | Тормозной путь |
|---|---|---|
| 20 миль / ч | 6 м + 6 м | 12 м (40 футов) |
| 30 миль / ч | 9м + 14м | 23 м (75 футов) |
| 40 миль / ч | 12м + 24м | 36 м (118 футов) |
| 50 миль / ч | 15м + 38м | 53 м (174 футов) |
Сколько длины автомобиля составляет безопасное расстояние?
Многие водители следуют «правилу трех секунд».Другими словами, вы должны держать расстояние в три секунды между вашим автомобилем и автомобилем перед вами, чтобы поддерживать безопасное расстояние следования.
Каков нормальный тормозной путь автомобиля, движущегося со скоростью 100 км / ч по мокрой дороге?
Тормозной путь на мокрой дороге
| Скорость | Расстояние реакции | Тормозной путь |
|---|---|---|
| 80 км / ч | 33 кв.м. | 52м |
| 90 км / ч | 38 кв.м. | 65 м |
| 100 км / ч | 42м | 80 м |
| 110 км / ч | 46 мес. | 97м |
Машину какой длины вы должны оставить?
На каждые десять миль в час приходится одна длина автомобиля, — сказал Барндт.«Так что, если вы едете со скоростью 55 миль в час, у вас должно быть расстояние в шесть машин, чтобы, если что-то случится с машиной перед вами, у вас было время остановиться или отреагировать». Пункт номер два, в котором, по словам Барндта, виновны все водители, — это отвлечение внимания.
Безопасно ли ехать в 3 часа ночи?
С полуночи до трех утра, говорится в новом отчете. Новый отчет Национального управления безопасности дорожного движения показал, что большинство дорожно-транспортных происшествий в состоянии алкогольного опьянения (55%) происходят между полуночью и 3 часами ночи. Три из четырех смертельных случаев связаны с вождением в состоянии алкогольного опьянения — с полуночи до 3 часов ночи.м. также самый смертоносный.
На сколько футов вы отстаете от машины?
500 футов
Что такое правило четырех секунд?
Основная цель правила 4 секунд — обеспечить, чтобы водители оставались как минимум на 4 секунды позади идущей впереди машины. Доказано, что 4 секунды — это достаточное расстояние для предотвращения столкновений, что противоречит предыдущим оценкам в 2–3 секунды.
Сколько длины автомобиля составляет 100 футов?
На автостраде это примерно шесть машин длины. Для нормальной скорости, которую вы едете, вы можете использовать одометр, чтобы измерить 100 ярдов (или метров) и посмотреть, сколько времени вам понадобится, чтобы преодолеть это расстояние, говоря что-то, что легко повторить.
 При движении поезда по руководящему спуску длина Т. п.,… … Технический железнодорожный словарь
При движении поезда по руководящему спуску длина Т. п.,… … Технический железнодорожный словарь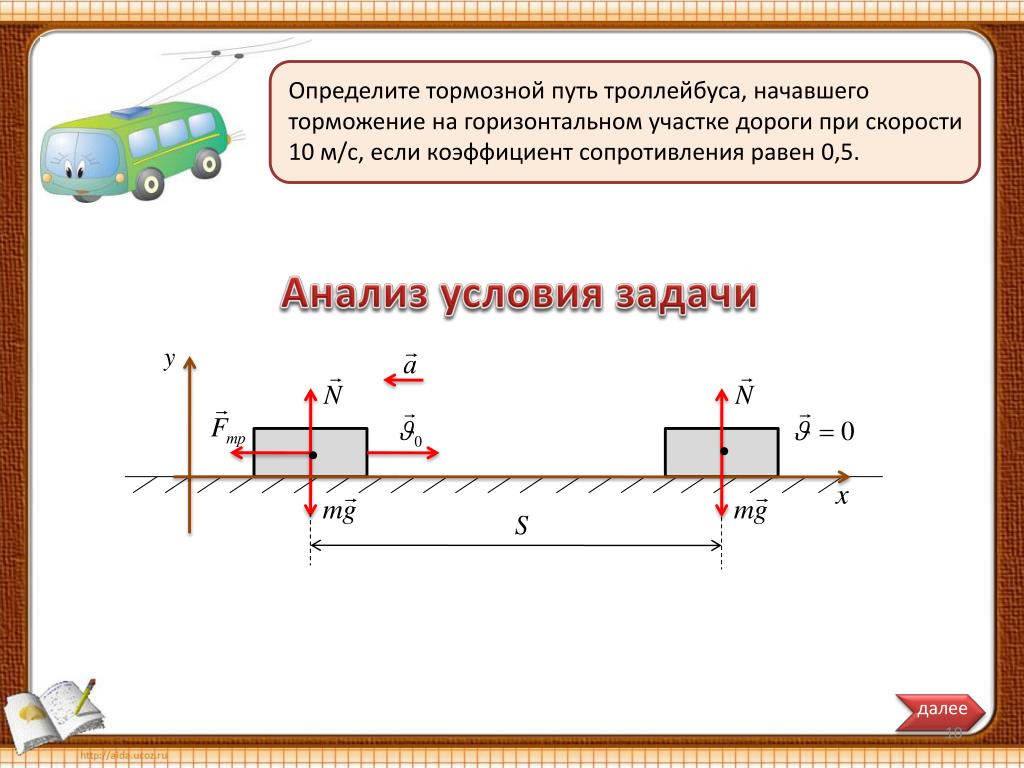 Зависит от эффективности тормозных механизмов, времени срабатывания привода и тормозов, скорости движения, силы сцепления колес с опорной поверхностью (дорога,… … Автомобильный словарь
Зависит от эффективности тормозных механизмов, времени срабатывания привода и тормозов, скорости движения, силы сцепления колес с опорной поверхностью (дорога,… … Автомобильный словарь [ГОСТ Р… … Словарь-справочник терминов нормативно-технической документации
[ГОСТ Р… … Словарь-справочник терминов нормативно-технической документации