Амперсанд — Википедия
Материал из Википедии — свободной энциклопедии
| Амперсанд | |
|---|---|
| & | |
Изображение | |
| ampersand | |
| Юникод | U+0026 |
| HTML-код | |
| UTF-16 | 0x26 |
| %26 | |
| Мнемоника | & |
Амперса́нд (&, иногда — амперсе́нд; англ. ampersand) — логограмма, заменяющая союз «и». Возник как лигатура буквосочетания et (с лат. — «и»).
Амперсанд прямого и курсивного начертанийАмперсанд является графическим сокращением (лигатурой) латинского союза et («и») — это хорошо видно на изображении амперсанда в курсивном начертании.
В «Кратких сведениях по типографскому делу» называется «знаком, заменяющим союз „и“», в «Справочнике технолога-полиграфиста» — «знаком конъюнкции», в «Справочной книге корректора и редактора» (1974) — «специальным компанейским знаком, разновидностью лигатуры»
Амперсанд со второй половины VIII века активно используется переписчиками, а с середины XV века — типографами.

Амперсанд стал настолько привычной частью письма в Европе и Северной Америке, что встал на последнее место в английском алфавите во всех букварях уже к началу XIX века (а пропадать из них стал только к началу XX века)[источник не указан 38 дней].
При произношении английского алфавита (например, при заучивании его в англоязычных школах) перед названиями букв, совпадавших с однобуквенными словами, произносили per se (с лат. — «сама по себе», «как таковая») для того, чтобы отличить букву от совпадающего с ней слова. Данная практика также использовалась при произношении слов по буквам: говорилось «I, per se I», чтобы не путать букву с английским местоимением «I» (то есть «я»). Последним знаком в алфавите шёл «&», и заканчивали произношение алфавита словами: «X, Y, Z, and per se and» («„экс“, „уай“, „зед“ и сама по себе „и“», «„и“ как таковая»). [2][3] В 1837 году в словарях было зафиксировано слово ampersand.
В русском языке[править | править код]
Союз «и» сам по себе короткий, и сокращение ему не нужно. Поэтому в СССР амперсанд ограниченно применялся в научно-технической документации для обозначения логической операции «и» (например, для логических элементов «И» в электрических схемах).
В информатике[править | править код]
Амперсанд в программном обеспечении:
В макроязыке Ассемблера ЕС ЭВМ амперсанд служит признаком параметра.
- В Microsoft Excel символ «&» используется как оператор сцепки текстовых значений.
- В языках Си, С++, Java, C#, JavaScript и других символ «&» применяется для обозначения нескольких операторов:
- для получения ссылки на переменную, унарный оператор, «&» должен предшествовать префиксом идентификатору (имени) переменной;
- оператор «&» обозначает побитовое «И»;
- оператор «&&» обозначает условное логическое И (проверка истинности последующего выражения только при условии истинности предшествующего).
- В GET (системе кодирования запросов HTTP) оператором «&» разделяются аргументы в строке запроса.
- В Бейсике символ &, стоящий сразу после имени переменной, означает тип переменной «длинное целое», а сочетание символов &H означает, что число записано в шестнадцатеричной системе счисления, а в Visual Basic, кроме того, с помощью операции & происходит конкатенация (объединение) строк.
- В SGML (в том числе HTML, XML) конструкция
&name;выводит символ по его названию. Её подвид&#xxxx;(где xxxx — число) выводит символ с кодом xxxx из юникод-пространства. - В большинстве командных интерпретаторов unix-подобных ОС команда, завершённая амперсандом, будет выполняться в «фоновом режиме».
Юникод содержит несколько вариантов амперсанда:
| Графема | Название | Юникод | HTML |
|---|---|---|---|
| & | AMPERSAND | U+0026 | & или & |
| ⅋ | TURNED AMPERSAND | U+214B | ⅋ |
| ﹠ | SMALL AMPERSAND | U+FE60 | ﹠ |
| & | FULLWIDTH AMPERSAND | U+FF06 | & |
| 🙰 | SCRIPT LIGATURE ET ORNAMENT | U+1F670 | 🙰 |
| 🙱 | HEAVY SCRIPT LIGATURE ET ORNAMENT | U+1F671 | 🙱 |
| 🙲 | LIGATURE OPEN ET ORNAMENT | U+1F672 | 🙲 |
| 🙳 | HEAVY LIGATURE OPEN ET ORNAMENT | U+1F673 | 🙳 |
| 🙴 | HEAVY AMPERSAND ORNAMENT | U+1F674 | 🙴 |
| 🙵 | SWASH AMPERSAND ORNAMENT | U+1F675 | 🙵 |
- Коломнин П. П. Краткие сведения по типографскому делу. СПб., 1899. 604 стр.
- Иванова О. Е., Лопатин В. В., Нечаева И. В. и др. Русский орфографический словарь: Около 180 тыс. слов / под ред. Лопатина В. В. 2-е изд., испр. и доп. М.: Изд-во Ин-т рус. яз. им. В. В. Виноградова, 2005. 960 стр. ISBN 5-88744-052-X.
- Справочник технолога-полиграфиста. Ч. 1. Наборные процессы / Сост. Шульмейстер М. В., Таль Г. А. М.: Книга, 1981. 255 стр.
- ГОСТ 2.743-91. Единая система конструкторской документации. Обозначения условные графические в схемах. Элементы цифровой техники
- Allan Haley. Ampersand (англ.). fonts.com
ru.wikipedia.org
| Символ (TeX) (Команда (TeX)) | Символ (Юникод) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| ⇒{\displaystyle \Rightarrow } (\Rightarrow) →{\displaystyle \rightarrow } (\rightarrow) ⊃{\displaystyle \supset } (\supset) | → ⊃ | Импликация, следование | A⇒B{\displaystyle A\Rightarrow B} означает «если A{\displaystyle A} верно, то B{\displaystyle B} также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒ или для обозначения надмножества, см. ниже.). | x=2⇒x2=4{\displaystyle x=2\Rightarrow x^{2}=4} верно, но x2=4⇒x=2{\displaystyle x^{2}=4\Rightarrow x=2} неверно (так как x=−2{\displaystyle x=-2} также является решением). |
| «влечёт» или «если…, то» или «отсюда следует» | ||||
| везде | ||||
| ⇔{\displaystyle \Leftrightarrow } (\Leftrightarrow) | ⇔ | Равносильность | A⇔B{\displaystyle A\Leftrightarrow B} означает «A{\displaystyle A} верно тогда и только тогда, когда B{\displaystyle B} верно». | x+5=y+2⇔x+3=y{\displaystyle x+5=y+2\Leftrightarrow x+3=y} |
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧{\displaystyle \wedge } (\wedge) | ∧ | Конъюнкция | A∧B{\displaystyle A\wedge B} истинно тогда и только тогда, когда A{\displaystyle A} и B{\displaystyle B} оба истинны. | (n>2)∧(n<4)⇔(n=3){\displaystyle (n>2)\wedge (n<4)\Leftrightarrow (n=3)}, если n{\displaystyle n} — натуральное число. |
| «и» | ||||
| Математическая логика | ||||
| ∨{\displaystyle \vee } (\vee) | ∨ | Дизъюнкция | A∨B{\displaystyle A\vee B} истинно, когда хотя бы одно из условий A{\displaystyle A} и B{\displaystyle B} истинно. | (n⩽2)∨(n⩾4)⇔n≠3{\displaystyle (n\leqslant 2)\vee (n\geqslant 4)\Leftrightarrow n\neq 3}, если n{\displaystyle n} — натуральное число. |
| «или» | ||||
| Математическая логика | ||||
| ¬{\displaystyle \neg } (\neg) | ¬ | Отрицание | ¬A{\displaystyle \neg A} истинно тогда и только тогда, когда ложно A{\displaystyle A}. | ¬(A∧B)⇔(¬A)∨(¬B){\displaystyle \neg (A\wedge B)\Leftrightarrow (\neg A)\vee (\neg B)} x∉S⇔¬(x∈S){\displaystyle x\notin S\Leftrightarrow \neg (x\in S)} |
| «не» | ||||
| Математическая логика | ||||
| ∀{\displaystyle \forall } (\forall) | ∀ | Квантор всеобщности | ∀x,P(x){\displaystyle \forall x,P\left(x\right)} обозначает «P(x){\displaystyle P\left(x\right)} верно для всех x{\displaystyle x}». | ∀n∈N,n2⩾n{\displaystyle \forall n\in \mathbb {N} ,\;n^{2}\geqslant n} |
| «Для любых», «Для всех», «Для всякого» | ||||
| Математическая логика | ||||
| ∃{\displaystyle \exists } (\exists) | ∃ | Квантор существования | ∃x,P(x){\displaystyle \exists x,\;P\left(x\right)} означает «существует хотя бы один x{\displaystyle x} такой, что верно P(x){\displaystyle P\left(x\right)}» | ∃n∈N,n+5=2n{\displaystyle \exists n\in \mathbb {N} ,\;n+5=2n} (подходит число 5) |
| «существует» | ||||
| Математическая логика | ||||
| ={\displaystyle =} | = | Равенство | x=y{\displaystyle x=y} обозначает «x{\displaystyle x} и y{\displaystyle y} обозначают одно и то же значение». | 1 + 2 = 6 − 3 |
| «равно» | ||||
| везде | ||||
| :={\displaystyle :=} :⇔{\displaystyle :\Leftrightarrow } | := :⇔
| Определение | x:=y{\displaystyle x:=y} означает «x{\displaystyle x} по определению равен y{\displaystyle y}». P:⇔Q{\displaystyle P:\Leftrightarrow Q} означает «P{\displaystyle P} по определению равносильно Q{\displaystyle Q}» | ch(x):=12(ex+e−x){\displaystyle {\rm {ch}}\left(x\right):={1 \over 2}\left(e^{x}+e^{-x}\right)} (определение гиперболического косинуса) A⊕B:⇔(A∨B)∧¬(A∧B){\displaystyle A\oplus B:\Leftrightarrow (A\vee B)\wedge \neg (A\wedge B)} (определение исключающего «ИЛИ») |
| «равно/равносильно по определению» | ||||
| везде | ||||
| {,}{\displaystyle \{,\}} | { } | Множество элементов | {a,b,c}{\displaystyle \{a,\;b,\;c\}} означает множество, элементами которого являются a{\displaystyle a}, b{\displaystyle b} и c{\displaystyle c}. | N={1,2,…}{\displaystyle \mathbb {N} =\{1,\;2,\;\ldots \}} (множество натуральных чисел) |
| «Множество…» | ||||
| Теория множеств | ||||
| {|}{\displaystyle \{|\}} | {|} | Множество элементов, удовлетворяющих условию | {x|P(x)}{\displaystyle \{x\,|\,P\left(x\right)\}} означает множество всех x{\displaystyle x} таких, что верно P(x){\displaystyle P\left(x\right)}. | {n∈N|n2<20}={1,2,3,4}{\displaystyle \{n\in \mathbb {N} \,|\,n^{2}<20\}=\{1,\;2,\;3,\;4\}} |
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| ∅{\displaystyle \varnothing } (\varnothing) {}{\displaystyle \{\}} | ∅ {} | Пустое множество | {}{\displaystyle \{\}} и ∅{\displaystyle \varnothing } означают множество, не содержащее ни одного элемента. | {n∈N|1<n2<4}=∅{\displaystyle \{n\in \mathbb {N} \,|\,1<n^{2}<4\}=\varnothing } |
| «Пустое множество» | ||||
| Теория множеств | ||||
| ∈{\displaystyle \in } (\in) ∉{\displaystyle \notin } (\notin) | ∈ ∉ | Принадлежность/непринадлежность к множеству | a∈S{\displaystyle a\in S} означает «a{\displaystyle a} является элементом множества S{\displaystyle S}» a∉S{\displaystyle a\notin S} означает «a{\displaystyle a} не является элементом множества S{\displaystyle S}» | 2∈N{\displaystyle 2\in \mathbb {N} } 12∉N{\displaystyle {1 \over 2}\notin \mathbb {N} } |
| «принадлежит», «из» «не принадлежит» | ||||
| Теория множеств | ||||
| ⊆{\displaystyle \subseteq } (\subseteq) ⊂{\displaystyle \subset } (\subset) | ⊆ ⊂ | Подмножество | A⊆B{\displaystyle A\subseteq B} означает «каждый элемент из A{\displaystyle A} также является элементом из B{\displaystyle B}». A⊂B{\displaystyle A\subset B} обычно означает то же, что и A⊆B{\displaystyle A\subseteq B}. Однако некоторые авторы используют ⊂{\displaystyle \subset }, чтобы показать строгое включение (то есть ⊊{\displaystyle \subsetneq }). | (A∩B)⊆A{\displaystyle (A\cap B)\subseteq A} Q⊆R{\displaystyle \mathbb {Q} \subseteq \mathbb {R} } |
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⊇{\displaystyle \supseteq } (\supseteq) ⊃{\displaystyle \supset } (\supset) | ⊇ ⊃ | Надмножество | A⊇B{\displaystyle A\supseteq B} означает «каждый элемент из B{\displaystyle B} также является элементом из A{\displaystyle A}». A⊃B{\displaystyle A\supset B} обычно означает то же, что и A⊇B{\displaystyle A\supseteq B}. Однако некоторые авторы используют ⊃{\displaystyle \supset }, чтобы показать строгое включение (то есть ⊋{\displaystyle \supsetneq }). | (A∪B)⊇A{\displaystyle (A\cup B)\supseteq A} R⊇Q{\displaystyle \mathbb {R} \supseteq \mathbb {Q} } |
| «является надмножеством», «включает в себя» | ||||
| Теория множеств | ||||
| ⊊{\displaystyle \subsetneq } (\subsetneq) | ⊊ | Собственное подмножество | A⊊B{\displaystyle A\subsetneq B} означает A⊆B{\displaystyle A\subseteq B} и A≠B{\displaystyle A\neq B}. | N⊊Q{\displaystyle \mathbb {N} \subsetneq \mathbb {Q} } |
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ⊋{\displaystyle \supsetneq } (\supsetneq) | ⊋ | Собственное надмножество | A⊋B{\displaystyle A\supsetneq B} означает A⊇B{\displaystyle A\supseteq B} и A≠B{\displaystyle A\neq B}. | Q⊋N{\displaystyle \mathbb {Q} \supsetneq \mathbb {N} } |
| «является собственным надмножеством», «строго включает в себя» | ||||
| Теория множеств | ||||
| ∪{\displaystyle \cup } (\cup) | ∪ | Объединение | A∪B{\displaystyle A\cup B} означает множество, содержащее все элементы из A{\displaystyle A} и B{\displaystyle B} | A⊆B⇔A∪B=B{\displaystyle A\subseteq B\Leftrightarrow A\cup B=B} |
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| ∩{\displaystyle \cap } (\cap) | ⋂ | Пересечение | A∩B{\displaystyle A\cap B} означает множество одинаковых элементов, принадлежащих и A{\displaystyle A}, и B{\displaystyle B}. | {x∈R|x2=1}∩N={1}{\displaystyle \{x\in \mathbb {R} \,|\,x^{2}=1\}\cap \mathbb {N} =\{1\}} |
| «Пересечение … и … «, «…, пересечённое с …» | ||||
| Теория множеств | ||||
| ∖{\displaystyle \setminus |
ru.wikipedia.org
| Символ | Расшифровка | Перевод |
| ` | acute, back quote, grave, grave accent, left quote, open quote | гравис, кавычка, обратный машинописный апостроф |
| ~ | tilde | тильда |
| ! | exclamation mark, exclamation point, bang | восклицательный знак |
| @ | at or at symbol | эт, коммерческое эт, «собака» |
| # | octothorpe, number, pound, sharp, hash | октоторп, решетка, диез |
| $ | dollar sign | знак доллара |
| % | percent | процент |
| ^ | caret, circumflex | циркумфлекс, знак вставки |
| & | ampersand, and | амперсанд |
| * | asterisk, star | астериск, звездочка, знак умножения |
| ( | open parenthesis | левая, открытая круглая скобка |
| ) | close parenthesis | правая, закрытая круглая скобка |
| — | hyphen, minus, dash | минус, дефис |
| _ | underscore | знак подчеркивания |
| = | equals | знак равенства |
| + | plus | плюс |
| [ | open or left square bracket | левая, открытая квадратная скобка |
| ] | close or right square bracket | правая, закрытая квадратная скобка |
| { | open or left curly brace | левая, открытая фигурная скобка |
| } | close or right curly brace | правая, закрытая фигурная скобка |
| ; | semicolon | точка с запятой |
| : | colon | двоеточие |
| ‘ | apostrophe, single quote | машинописный апостроф, одинарная кавычка |
| « | quote, quotation mark | двойная кавычка |
| , | comma | запятая |
| . | period, dot | точка |
| / | forward slash | слэш, косая черта, знак дроби |
| < | less than, open or left angle bracket | левая, открытая угловая скобка, знак меньше |
| > | greater than, close or right angle bracket | правая, закрытая угловая скобка, знак больше |
| ? | question mark | вопросительный знак |
| \ | backslash | обратный слэш, обратная косая черта |
| | | pipe, vertical bar | вертикальная черта |
| § | section | параграф |
inf-95.blogspot.com
| Символ (TeX) | Символ (Unicode) | Название | Значение | Пример |
|---|---|---|---|---|
| Произношение | ||||
| Раздел математики | ||||
| ⇒ → ⊃ | Импликация, следование | означает «если верно, то также верно». (→ может использоваться вместо ⇒ или для обозначения функции, см. ниже.) (⊃ может использоваться вместо ⇒, или для обозначения надмножества, см. ниже.). | верно, но неверно (так как также является решением). | |
| «влечёт» или «если…, то» | ||||
| везде | ||||
| ⇔ | Равносильность | означает « верно тогда и только тогда, когда верно». | ||
| «если и только если» или «равносильно» | ||||
| везде | ||||
| ∧ | Конъюнкция | истинно тогда и только тогда, когда и оба истинны. | , если — натуральное число. | |
| «и» | ||||
| Математическая логика | ||||
| ∨ | Дизъюнкция | истинно, когда хотя бы одно из условий и истинно. | , если — натуральное число. | |
| «или» | ||||
| Математическая логика | ||||
| ¬ | Отрицание | истинно тогда и только тогда, когда ложно . | ||
| «не» | ||||
| Математическая логика | ||||
| ∀ | Квантор всеобщности | обозначает « верно для всех ». | ||
| «Для любых», «Для всех» | ||||
| Математическая логика | ||||
| ∃ | Квантор существования | означает «существует хотя бы один такой, что верно » | (подходит число 5) | |
| «существует» | ||||
| Математическая логика | ||||
| = | Равенство | обозначает « и обозначают одно и то же значение». | 1 + 2 = 6 − 3 | |
| «равно» | ||||
| везде | ||||
| := :⇔ | Определение | означает « по определению равен ». означает « по определению равносильно » | (Гиперболический косинус) (Исключающее или) | |
| «равно/равносильно по определению» | ||||
| везде | ||||
| { , } | Множество элементов | означает множество, элементами которого являются , и . | (множество натуральных чисел) | |
| «Множество…» | ||||
| Теория множеств | ||||
| { | } { : } | Множество элементов, удовлетворяющих условию | означает множество всех таких, что верно . | ||
| «Множество всех… таких, что верно…» | ||||
| Теория множеств | ||||
| ∅ {} | Пустое множество | и означают множество, не содержащее ни одного элемента. | ||
| «Пустое множество» | ||||
| Теория множеств | ||||
| ∈ ∉ | Принадлежность/непринадлежность к множеству | означает « является элементом множества » означает « не является элементом множества » | ||
| «принадлежит», «из» «не принадлежит» | ||||
| Теория множеств | ||||
| ⊆ ⊂ | Подмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является подмножеством», «включено в» | ||||
| Теория множеств | ||||
| ⊇ ⊃ | Надмножество | означает «каждый элемент из также является элементом из ». обычно означает то же, что и . Однако некоторые авторы используют , чтобы показать строгое включение (то есть ). | ||
| «является надмножеством», «включает в себя» | ||||
| Теория множеств | ||||
| ⊊ | Собственное подмножество | означает и . | ||
| «является собственным подмножеством», «строго включается в» | ||||
| Теория множеств | ||||
| ⊋ | Собственное надмножество | означает и . | ||
| «является собственным надмножеством», «строго включает в себя» | ||||
| Теория множеств | ||||
| ∪ | Объединение | означает множество элементов, принадлежащих или (или обоим сразу). | ||
| «Объединение … и …», «…, объединённое с …» | ||||
| Теория множеств | ||||
| ⋂ | Пересечение | означает множество элементов, принадлежащих и , и . | ||
| «Пересечение … и … », «…, пересечённое с …» | ||||
| Теория множеств | ||||
| \ | Разность множеств | означает множество элементов, принадлежащих , но не принадлежащих . | ||
| «разность … и … », «минус», «… без …» | ||||
| Теория множеств | ||||
| → | Функция | означает функцию с областью определения и областью прибытия (областью значений) . | Функция , определённая как | |
| «из … в», | ||||
| везде | ||||
| ↦ | Отображение | означает, что образом после применения функции будет . | Функцию, определённую как , можно записать так: | |
| «отображается в» | ||||
| везде | ||||
| N или ℕ | Натуральные числа | означает множество или реже (в зависимости от ситуации). | ||
| «Эн» | ||||
| Числа | ||||
| Z или ℤ | Целые числа | означает множество | ||
| «Зед» | ||||
| Числа | ||||
| Q или ℚ | Рациональные числа | означает | ||
| «Ку» | ||||
| Числа | ||||
| R или ℝ | Вещественные числа, или действительные числа | означает множество всех пределов последовательностей из | ( — комплексное число: ) | |
| «Эр» | ||||
| Числа | ||||
| C или ℂ | Комплексные числа | означает множество | ||
| «Це» | ||||
| Числа | ||||
| < > | Сравнение | обозначает, что строго меньше . означает, что строго больше . | ||
| «меньше чем», «больше чем» | ||||
| Отношение порядка | ||||
| ≤ или ⩽ ≥ или ⩾ | Сравнение | означает, что меньше или равен . означает, что больше или равен . | ||
| «меньше или равно»; «больше или равно» | ||||
| Отношение порядка | ||||
| ≈ | Приблизительное равенство | с точностью до означает, что 2,718 отличается от не больше чем на . | с точностью до . | |
| «приблизительно равно» | ||||
| Числа | ||||
| √ | Арифметический квадратный корень | означает неотрицательное действительное число, которое в квадрате даёт . | ||
| «Корень квадратный из …» | ||||
| Числа | ||||
| ∞ | Бесконечность | и суть элементы расширенного множества действительных чисел. Эти символы обозначают числа, меньшее/большее всех действительных чисел. | ||
| «Плюс/минус бесконечность» | ||||
| Числа | ||||
| | | | Модуль числа (абсолютное значение), модуль комплексного числа или мощность множества | обозначает абсолютную величину . обозначает мощность множества и равняется, если конечно, числу элементов . | ||
| «Модуль»; «Мощность» | ||||
| Числа и Теория множеств | ||||
| ∑ | Сумма, сумма ряда | означает «сумма , где принимает значения от 1 до », то есть . означает сумму ряда, состоящего из . | ||
| «Сумма … по … от … до …» | ||||
| Арифметика, Математический анализ | ||||
| ∏ | Произведение | означает «произведение для всех от 1 до », то есть | ||
| «Произведение … по … от … до …» | ||||
| Арифметика | ||||
| ! | Факториал | означает «произведение всех натуральных чисел от 1 до включительно, то есть | ||
| « факториал» | ||||
| Комбинаторика | ||||
| ∫ | Интеграл | означает «интеграл от до функции от по переменной ». | ||
| «Интеграл (от … до …) функции … по (или d)…» | ||||
| Математический анализ | ||||
| df/dx f'(x) | Производная | или означает «(первая) производная функции от по переменной ». | ||
| «Производная … по …» | ||||
| Математический анализ | ||||
| Производная -го порядка | или (во втором случае если — фиксированное число, то оно пишется римскими цифрами) означает «-я производная функции от по переменной ». | |||
| «-я производная … по …» | ||||
| Математический анализ |
dic.academic.ru
7 известных символов, о значении которых мы и не догадывались
Ребята, мы вкладываем душу в AdMe.ru. Cпасибо за то,
что открываете эту
красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook и ВКонтакте
Каждый день мы видим тысячи знаков и обозначений. А некоторые из них даже используем для выражения самых сильных чувств, когда не можем подобрать слова. Но задумывались ли вы, откуда они возникли? И правильно ли вообще мы их используем?
AdMe.ru решил подробно в этом разобраться и собрал для вас 7 самых известных символов, о значении и происхождении которых известно далеко не каждому.
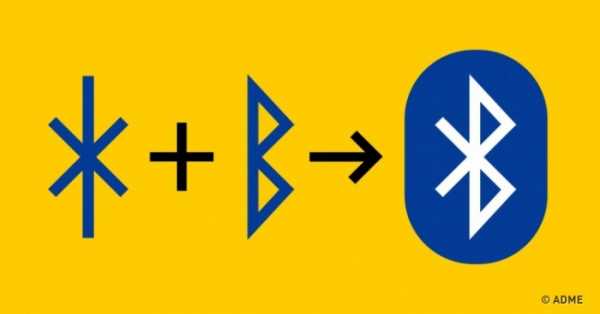
Амперсанд (знак &)
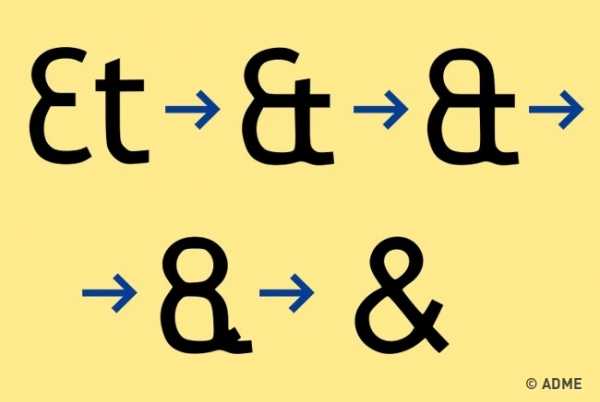
Знак амперсанд (&) обозначает латинский союз et (или английский and), то есть «и». Такую лигатуру придумали еще в Древнем Риме. Тирон, который был личным секретарем Цицерона, изобрел свою систему сокращений для ускорения письма, называемую «тироновскими знаками».
Впоследствии этот знак настолько прижился в Европе и Америке, что долгое время стоял на последнем месте в английском алфавите, а пропадать начал только к началу ХХ века. Само слово «амперсанд» — это сокращение фразы And per se and. Когда детям произносили буквы алфавита, то после z учитель говорил: Аnd per se and — «И само по себе «и». Перед буквой, совпадающей по произношению со словом, говорили per se («сама по себе», «как таковая»).
Со временем от букв et форма символа изменилась до такой степени, что возник такой знак.
Сердце
www.adme.ru
Как в разных странах называют символ «@» | Блогер RoseJustrose на сайте SPLETNIK.RU 11 ноября 2015

Итак, @ — лигатура, означающая «at». Официальное название символа — коммерческое at. В настоящее время в русском языке данный символ чаще всего называется «собака» , особенно при использовании его в сетевых сервисах. Иногда этот символ ошибочно называют амперсандом (&).
В бывшем СССР этот знак был неизвестен до появления компьютера.
Название «собака» получило распространение в связи с появлением на ЭВМ игры, где символ @ бегал по экрану и по сценарию игры означал собаку.
Другая версия происхождения названия: на алфавитно-цифровых мониторах персональных компьютеров серии ДВК (1980-е годы) «хвостик» рисуемого на экране изображения этого символа был очень коротким, что придавало ему сходство со схематически нарисованной собачкой.Вроде это ДВК-1
В то же время, в переводе с татарского (и некоторых других тюркских языков на территории бывшего СССР) «эт» означает — «собака».
В России пользователи чаще всего называют символ @ собакой, из-за чего адреса электронной почты, образованные от личных имен и фамилий, приобретают иной раз необычное звучание звучание. В 1990-е годы, когда значок @ впервые пытались перевести на русский, существовало множество равноправных вариантов — «кракозябра», «закорючка», «лягушка», «ухо» и другие. Правда, в настоящее время они практически исчезли.
В других странах нашу собачку тоже называют очень искусно и фантазийно. Поехали!
в Голландии – «обезьяний хвост»А что, если у обезьянки хвостик такой?
в Польше, Хорватии, Румынии – «обезьяна»А авторских не будет?
в Финляндии – «кошкин хвост»
во Франции – «улиточка»
в Венгрии – «гусеничка», «червячок» и «поросячий хвостик» Однажды, гуляя по лесу, заметила такую у себя на рукаве… Звонили из Китая, просили перестать так орать.
в Сербии — «лудо A» (чокнутая A) Кто помнит? )))
в Японии — «водоворот» или «наруто» (по названию водоворота Наруто) Появляется он один раз в сутки, когда воды Тихого океана устремляются в узкий пролив. Скорость вращения водоворота доходит до 20 км/ч. Диаметр воронки — до 15 м.
Появляется он один раз в сутки, когда воды Тихого океана устремляются в узкий пролив. Скорость вращения водоворота доходит до 20 км/ч. Диаметр воронки — до 15 м.
в Израиле – «штрудель»Как хочется сладенького!
в Китае – «мышонок»
в Норвегии – «канельболле» (спирально закрученная булочка с корицей, то есть плюшка)Булочка с корицей по-норвежски
В Германии знак дословно называют «обезьяна с цепким хвостом» , но немецкое слово Klammeraffe имеет также второе, переносное, значение: так называют пассажира на мотоцикле, сгорбившегося на втором сиденье за спиной водителя. Обожаю немецкий язык, наслаждение для меня!
В Швеции и Дании – «хобот слона» или «а с хоботом»
в Испании – сравнивают со спиралеобразной конфетой, популярной на острове МайоркаЭнсаймада — сладкий символ Майорки
в Чехии и Словакии — рольмопс (сельдь под маринадом) Кстати, это блюдо распространено во многих европейских странах, например в Германии, Латвии и Норвегии
Кстати, это блюдо распространено во многих европейских странах, например в Германии, Латвии и Норвегии
в Беларуси, Украине, Италии — «улитка»
Даже на международном языке эсперанто символ электронной почты получил свое название: «улитка». В общем, почти везде этот символ назвали тем или иным словом по принципу сходства. А у нас нет! Мне кажется, так интересней)) Загадочней!
Всем удачного дня! 
www.spletnik.ru
Как называется знак & где и зачем используют этот символ
Необычный, в то же время, привычный символ «&». Как называется эта закорючка – «&», так часто используемая даже в русском языке? Где и с какой целью пишут этот знак? Кто и зачем придумал символ «&»? Какой союз можно заменять знаком «&» и все поймут, что вы имели ввиду?
Знак «&» называется красивым словом — «амперсанд». Образовано от английского «and per se and», что в переводе обозначает «как таковой и».
Символ & — используется в качестве дубля союза «и» или английского «and». Несколько сотен лет назад, амперсанд был последней буквой английского алфавита и являлся полноправным союзом-буквой, обозначающим соединение чего-либо.
Зачем используют амперсанд «&» в современное время – история возникновения
Ответ на этот вопрос лежит в далеком прошлом. Первостепенно, знак «&» появился в языке программирования на заре развития века технологий. Он нес исключительно практичную миссию – сокращение союза «and» — пер. «и». Зачем?

Все дело в том, что английский союз «И» состоит из трех букв «AND». Такое длинное слово было крайне непрактично использовать в написании кодов программирования, учитывая его частоту употребления – больше, чем любое другое слово. Для экономии места (уменьшения веса кода) – и был придуман забавный символ «&».
В современность амперсанд «зашел» исключительно из-за своего внешнего вида. Как утверждают дизайнеры, он наиболее гармонично вписывается в любую рекламную вывеску, коллаж.
Правдивая история возникновения амперсанда – откуда «&» появился на самом деле
Еще одна теория возникновения чудного значка «&» амперсанд — отдана секретарю древнеримского политического деятеля Цицерона – Марку Туллию Тирону. Как гласит история, Марк решил сократить латинский союз «ET», в переводе означающий «И», таким неприметным знаком из-за большого объема письма.
Подобная закорючка не выделялась из общего текста, так как вся древнеримская письменность имела подобный внешний вид.
Историки утверждают, что эта теория возникновения амперсанда наиболее верная, т.к. была замечена ранее. Лишь в последствии, знак «пришелся кстати» и его стали использовать в программировании и дизайне рекламы.
Кто использует амперсанд в имени бренда – типографический знак в жизни
Как уже было написано ранее, после постоянного написания символа амперсанд в программировании, он стал широко использоваться в типографии. И действительно, символ имеет стильный, мягкий и лаконичный внешний вид. Отлично вписывается между любых слов и выражений.
Именно так подумали создатели брендов: M&M, Dolce&Gabbana, Mark & Spenser и т.д.

Теперь вы знаете, как называется знак & — расскажите об этом друзьям! Кстати, амперсанд есть на клавиатуре почти каждого компьютера. Она расположен на цифре 7, используя английскую раскладку.
kak-nazyvaetsya.ru