Какие силы действуют на автомобиль: Силы действующие на автомобиль при движении

Содержание

Силы действующие на автомобиль при движении

На движущийся автомобиль действует ряд сил, часть из которых направлена по оси движения автомобиля, а часть — под углом к этой оси. Условимся называть первые из этих сил продольными, а вторые боковыми.

Продольные силы могут быть направлены как по ходу, так и против хода движения автомобиля. Силы, направленные по ходу движения, являются движущимися и стремятся продолжить движение. Силы, направленные против хода движения, являются силами сопротивления и стремятся остановить автомобиль.

На автомобиль, движущийся по горизонтальному и прямому участку дороги, действуют следующие продольные силы:

При движении автомобиля в гору возникает сила сопротивления подъему, а при разгоне автомобиля—сила сопротивления разгону (сила инерции).

Тяговая сила

Развиваемый двигателем автомобиля крутящий момент передается на ведущие колеса.

В передаче крутящего момента от двигателя к ведущим колесам участвуют механизмы трансмиссии. Крутящий момент на ведущих колесах зависит от крутящего момента двигателя и передаточных чисел коробки передач и главной передачи. В точке касания колес с поверхностью дороги крутящий момент вызывает окружную силу. Противодействие дороги этой окружной силе выражается реактивной силой, передаваемой от дороги на ведущее колесо. Эта сила направлена в сторону движения автомобиля и называется толкающей или тяговой силой. Тяговая сила от колес передается на ведущий мост и далее на раму, заставляя автомобиль двигаться. Величина тяговой силы тем больше, чем больше крутящий момент двигателя и передаточные числа коробки передач и главной передачи. Тяговая сила на ведущих колесах достигает наибольшей величины при движении автомобиля на низшей передаче, поэтому низшую передачу используют при трогании с места автомобиля с грузом, при движении автомобиля по бездорожью. Величина тяговой силы на ведущих колесах автомобиля ограничивается сцеплением шин с поверхностью дороги.

Сила сцепления колес с дорогой

Трение, возникающее между ведущими колесами автомобиля и дорогой, называется силой сцепления. Сила сцепления равна произведению коэффициента сцепления на сцепной вес, т. е. вес, приходящийся на ведущие колеса автомобиля. Величина коэффициента сцепления шин с дорогой зависит от качества и состояния дорожного покрытия, формы и состояния рисунка протектора шины, давления воздуха в шине.

У легковых автомобилей полный вес распределяется по осям примерно поровну. Поэтому сцепной вес его можно принять равным 50% полного веса. У грузовых автомобилей при полной их нагрузке сцепной вес (вес, приходящийся на заднюю ось) составляет примерно 60—70% полного веса.

Величина коэффициента сцепления имеет большое значение для эксплуатации автомобиля и безопасности движения, так как от него зависят проходимость автомобиля, тормозные качества, возможность, пробуксовки и заноса ведущих колес. При незначительном коэффициенте сцепления трогание автомобиля с места сопровождается пробуксовкой, а торможение — скольжением колес. В результате автомобиль иногда не удается тронуть с места, а при торможении происходит резкое увеличение тормозного пути и возникновение заноса.

На асфальтобетонных покрытиях в жаркую погоду на поверхность выступает битум, делая дорогу маслянистой и более скользкой, что снижает коэффициент сцепления. Особенно сильно снижается коэффициент сцепления при смачивании дороги первым дождем, когда образуется еще не смытая пленка жидкой грязи. Заснежённая или обледенелая дорога особенно опасна в теплую погоду, когда поверхность подтаивает.

При увеличении скорости движения коэффициент сцепления снижается, в особенности на мокрой дороге, так как выступы рисунка протектора шины не успевают продавливать пленку влаги.

Исправное состояние рисунка протектора шины имеет большое значение при движении по грунтовым дорогам, снегу, песку, а также по дорогам с твердым покрытием, по покрытым пленкой грязи или воды. Благодаря наличию выступов рисунка опорная площадь шины уменьшается и, следовательно, возрастает удельное давление на поверхность дороги. При этом легче продавливается грязевая пленка и восстанавливается контакт с дорожным покрытием, а на легком грунте происходит непосредственное зацепление выступов рисунка за грунт.

Повышенное давление воздуха в шине уменьшает ее опорную поверхность, вследствие чего удельное давление возрастает настолько, что при трогании с места и при торможении может произойти разрушение резины и сцепление колес с дорогой уменьшается.

Таким образом, величина коэффициента сцепления зависит от многих условий и может изменяться в довольно значительных пределах. Так как много дорожно-транспортных происшествий происходит из-за плохого сцепления, то водители должны уметь приблизительно оценивать величину коэффициента сцепления и выбирать скорость движения и приемы управления в соответствии с ним.

Сила сопротивления воздуха

При движении автомобиль преодолевает сопротивление воздуха, которое складывается из нескольких сопротивлений:

лобового сопротивления (около 55—60% всего сопротивления воздуха)
создаваемого выступающими частями—подножками автобуса или автомобиля, крыльями (12—18%)
возникающего при прохождении воздуха через радиатор и подкапотное пространство (10—15%) и др.

Передней частью автомобиля воздух сжимается и раздвигается, в то время как в задней части автомобиля создается разрежение, которое вызывает образование завихрений.

Сила сопротивления воздуха зависит от величины лобовой, поверхности автомобиля, его формы, а также от скорости движения. Лобовую площадь грузового автомобиля определяют как произведение колеи (расстояние между шинами) на высоту автомобиля. Сила сопротивления воздуха возрастает пропорционально квадрату скорости движения автомобиля (если скорость возрастает в 2 раза, то сопротивление воздуха увеличивается в 4 раза).

Для улучшения обтекаемости и уменьшения сопротивления воздуха ветровое стекло автомобиля располагают наклонно, а выступающие детали (фары, крылья, ручки дверей) устанавливают заподлицо с внешними очертаниями кузова. У грузовых автомобилей можно уменьшить силу сопротивления воздуха, закрыв грузовую платформу брезентом, натянутым между крышей кабины и задним бортом.

Сила сопротивления качению

На каждое колесо автомобиля постоянно действует вертикальная нагрузка, которая вызывает вертикальную реакцию дороги.

При движении автомобиля на него действует сила сопротивления качению, которая возникает вследствие деформации шин и дороги и трения шин о дорогу.

Сила сопротивления качению равна произведению полного веса автомобиля на коэффициент сопротивления качению шин, который зависит от давления воздуха в шинах и качества дорожного покрытия. Вот- некоторые значения коэффициента сопротивления качению шин:

для асфальтобетонного покрытия— 0,014—0,020
для гравийного покрытия—0,02—0,025
для песка—0,1—0,3

Сила сопротивления подъему

Автомобильная дорога состоит из чередующихся между собой подъемов и спусков и редко имеет горизонтальные участки большой длины.

При движении на подъем автомобиль испытывает дополнительное сопротивление, которое зависит от угла наклона дороги к горизонту. Сопротивление подъему тем больше, чем больше вес автомобиля и угол наклона дороги.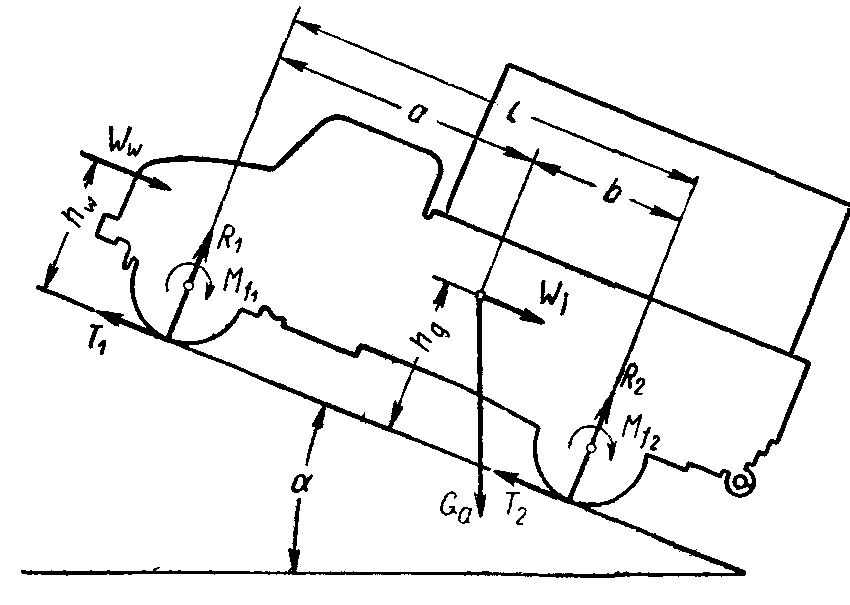 При подъезде к подъему необходимо правильно оценить возможности преодоления подъема. Если подъем непродолжительный, его преодолевают с разгоном автомобиля перед подъемом. Если подъем продолжительный, его преодолевают на пониженной передаче, переключившись на нее у начала подъема.

При движении автомобиля на спуске сила сопротивления подъему направлена в сторону движения и является движущей силой.

Сила сопротивления разгону

Часть тяговой силы при разгоне затрачивается на ускорение вращающихся масс, главным образом маховика коленчатого вала двигателя и колес автомобиля. Для того чтобы автомобиль начал двигаться с определенной скоростью, ему необходимо преодолеть силу сопротивления разгону, равную произведению массы автомобиля на ускорение. При разгоне автомобиля сила сопротивления разгону направлена в сторону, обратную движению. При торможении автомобиля и замедлении его движения эта сила направлена в сторону движения автомобиля.

Бывают случаи, когда при резком разгоне груз или пассажиры падают из открытого кузова, с сидений мотоцикла, а при резком торможении пассажиры ударяются о лобовое стекло или о передний борт автомобиля. Для того чтобы таких случаев не было, необходимо, плавно увеличивая частоту вращения коленчатого вала двигателя, преодолевать силу сопротивления разгону и плавно осуществлять торможение автомобиля.

Центр тяжести

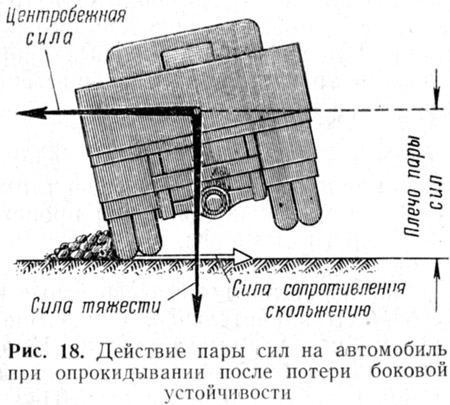
На автомобиль, как и на любое другое тело, действует сила тяжести, направленная вертикально вниз. Центром тяжести автомобиля называют такую точку автомобиля, от которой вес автомобиля распределяется равномерно во всех направлениях. У автомобиля центр тяжести располагается между передней и задней осью на высоте около 0,6 м для легковых и 0,7—1,0 м для грузовых. Чем ниже расположен центр тяжести, тем устойчивее автомобиль против опрокидывания. При загрузке автомобиля грузом центр тяжести поднимается у легковых автомобилей примерно на 0,3—0,4 м, а у грузовых на 0,5 м и более в зависимости от рода груза.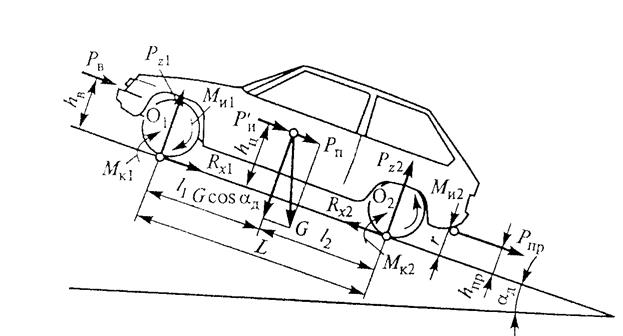 При неравномерном укладывании груза центр тяжести может также сместиться вперед, назад или в сторону, при этом будут нарушаться устойчивость автомобиля и легкость управления.

Силы, действующие на автомобиль

Кимстач В.В. 1

1ГБПОУ ЛО «Мичуринский многопрофильный техникум»

Козырева А.Г. 1

1ГБПОУ ЛО «Мичуринский многопрофильный техникум»

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение

Нашу современную жизнь трудно представить без автомобиля. Нет такой профессии на Земле, представитель которой не нуждался бы в автомобиле. На автомобиле или на автобусе мы добираемся до места назначения. Когда выходишь из дома, то почти сразу мы видим автомобиль.

Первый автотранспорт был изобретен много лет назад. Он восхищал своей эксклюзивностью и новаторством. Сейчас в мире представлены тысячи различных моделей машин, которые рассчитаны на разных потребителей. Но часто ли водители задумываются над следующими вопросами.

Каковы причины движения автомобиля? Какие силы действуют на автомобиль?

В нашей работе мы попытаемся ответить на это вопросы, используя специальную литературу. Рассмотрим какие внешние силы действуют на автомобиль во время движения по прямой и наклонной поверхности. Определим какие силы препятствуют, а какие способствуют движению автомобиля. Отдельное внимание уделим процессу торможения, так как с помощью тормозов можно не только остановить и удержать машину на месте, но и преодолеть скользкий участок, опасный поворот, развернуться и даже перескочить неширокую канаву или выбоину.

Силы, действующие на автомобиль

Автомобиль, преодолевающий подъем, одновременно движется вверх и вперед. В общем случае на подъеме при ускоренном перемещении автомобиля на него действуют силы, движущие его, силы оказывающие сопротивление движению автомобиля, и силы, составляющие нормальные реакции дороги на передние Z_п и задние Z_з колеса, вызванные перпендикулярной плоскости дороги составляющей силы тяжести автомобиля.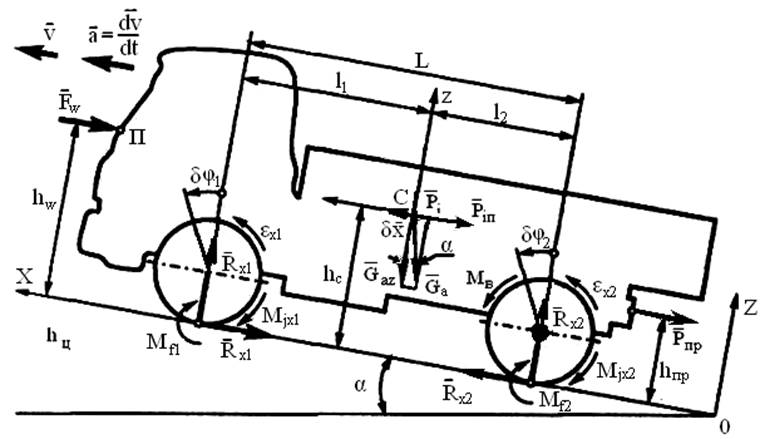

Покрышка соприкасается с дорогой бесконечно большим числом точек. В каждой из этих точек на покрышку действует бесконечно малая сила — элементарная реакция дороги. Равнодействующую элементарных сил, которая действует со стороны дороги на колесо в области контакта, называют реакцией дороги.

Силы, движущие автомобиль, возникают в результате взаимодействия ведущих колес автомобиля с дорогой и называются силами тяги F_т (рис. 1).

К силам, оказывающим сопротивление движению автомобиля, относятся силы сопротивления качению передних Р_ск.п. и задних Р_ск.з. колес, действующие в плоскости дороги; сила сопротивления подъему Р_сп, сила сопротивления воздуха F_св, сила инерции F_и, приложенная к центру масс ЦМ автомобиля и называемая силой сопротивления разгону.

Силы Z_п и Z_з составляют нормальные реакции дороги на передние и задние колеса соответственно. Они вызваны перпендикулярной плоскости дороги, составляющей GN силы тяжести G автомобиля с полной нагрузкой.

Рис.1

Рис.1. Внешние силы, действующие на автомобиль во время движения: ЦМ- центр масс; G — Сила тяжести автомобиля с полной нагрузкой;

GN — составляющая силы тяжести, перпендикулярная плоскости дороги; Р_сп^_ сила сопротивления подъему; Р_ск.п, Р_ск.з— сила сопротивления качению передних и задних колес; F_св — сила сопротивления воздуха; F_т — сила тяги; F_и^—сила инерции; a — угол, характеризующий крутизну подъема; Н- превышение дороги; S- заложение дороги; Zn, Z_з— нормальные реакции дороги на передние и задние колеса.

Сила сопротивления качению

Сила сопротивления качениюР_ск постоянно мешает движению и представляет собой целую совокупность сил. Это силы, деформирующие и перемещающие грунт; деформирующие шины; силы трения колес о колею; силы, образующиеся при преодолении выбоин, и т.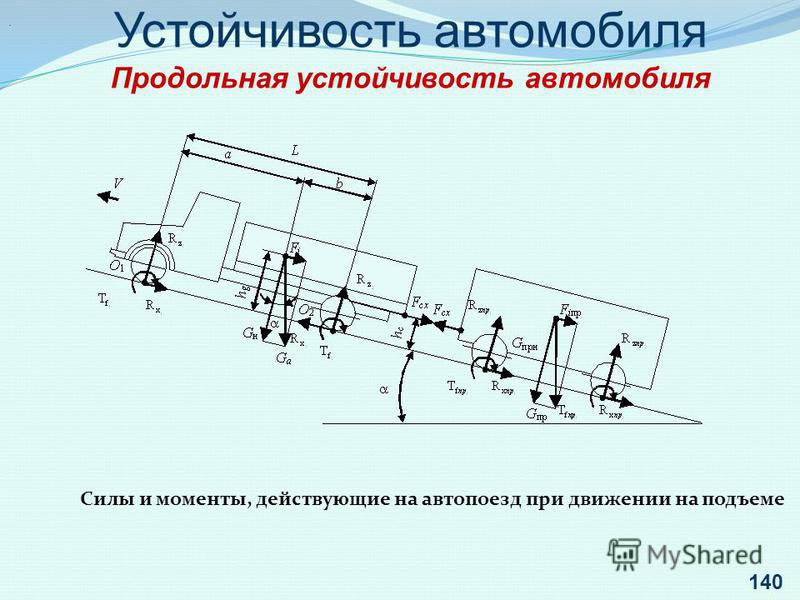 п.

Принято считать, что:

Р_ск = f·G,

где: Р_ск — сила сопротивления качению;

f = 0,015 — 0,3 — коэффициент сопротивления качению, учитывающий состояние дороги, давление в шинах и пр.;

G — сила тяжести автомобиля.

Сила сопротивления качению Р_ск составляет подобающую долю от силы тяжести автомобиля.

Сила сопротивления подъему

Сила сопротивления подъемуР_сп— Крутизну подъема охарактеризовывают углом в градусах (см. рис. 1) или же уклоном дороги i, который представляет собой отношение превышения Н дороги к заложению S, т. е. Силу тяжести G автомобиля, преодолевающего подъем, можно разложить на две составляющие: на силу Р_сп, параллельную дороге, и силу Gn=G-cosα, перпендикулярную ей.

Силу Р_сп= G-sinα, называют силой сопротивления подъему, где

Также силу сопротивления подъему выражают формулой

При перемещении на спуске сила Р_сп ориентирована в сторону перемещения автомобиля и, следовательно, меняет свой знак (рис.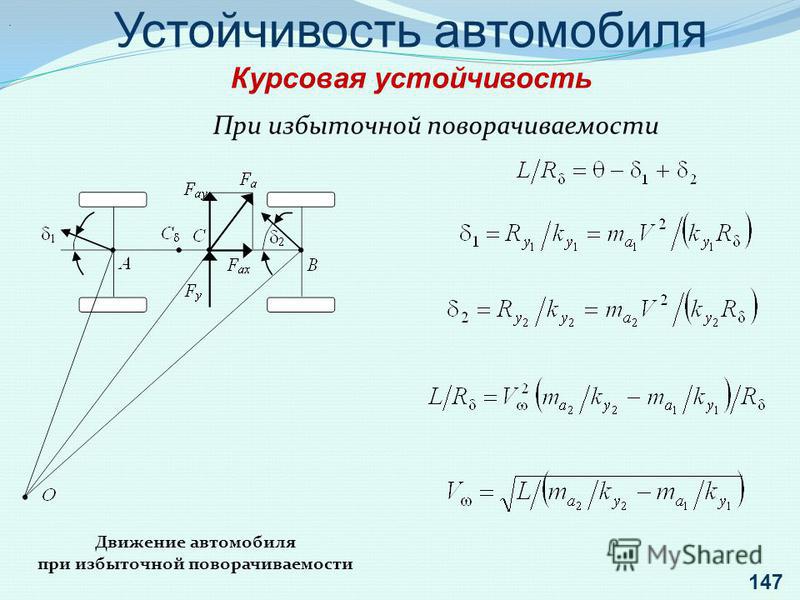 1, в) и, в отличие от силы сопротивления качению, может стать и движущей. Вследствие этого угол а и уклон дороги i считают положительными при перемещении автомобиля на подъеме и отрицательными при его перемещении на спуске.

При перемещении автомобиля на подъеме силу Р_сп можно объединить с Р_ск, а поскольку обе эти силы пропорциональны силе тяжести автомобиля, то:

При перемещении автомобиля под уклон

Сила сопротивления воздуха (аэродинамическое сопротивление)

Сила сопротивления воздуха F_св— данная сила считается следствием давления встречных частиц воздуха на движущийся автомобиль, разрежения, образующегося позади автомобиля, завихрения воздуха вокруг автомобиля и трения воздуха о поверхность автомобиля. В каждой точке поверхности автомобиля в итоге соприкосновения его с воздушной средой появляются элементарные силы, нормальные к поверхности и касательные к ней. Для упрощения расчетов элементарные силы сопротивления воздуха, распределенные по всей поверхности автомобиля, заменяют сосредоточенной силой сопротивления воздуха F_CB. Опытным путем установлено, что сила сопротивления воздуха равна

k_в — коэффициент сопротивления воздуха, зависящий от формы и качества отделки поверхности автомобиля 0,20 — 0,30H·m⁴;

S_л — лобовая площадь автомобиля;

V — скорость движения автомобиля.

Из формулы видно, что сопротивление воздуха находится в зависимости от скорости автомобиля, его обтекаемости, величины площади поперечного сечения, плотности воздуха. Существенное значение F_св приобретает только при высоких скоростях, так как зависит от квадрата скорости.

Сила, разгоняющая автомобиль.

Для автомобиля характерным считается неравномерное движение. Показателями разгона являются ускорение, время и путь разгона. В общем случае перемещения автомобиля сила тяги F_т уравновешивается силами сопротивления перемещения:

При разгоне автомобиля, т. е. при перемещении автомобиля с ускорением а, появляется сила инерции F_и автомобиля, противодействующая разгону, равная

где m — масса автомобиля;

а — ускорение автомобиля.

Влияние инерционного момента вращающихся масс учитывается коэффициентом  относительного увеличения массы автомобиля, предусматривающим воздействие вращающихся масс, показывающим, во сколько раз сила, необходимая для ускорения автомобиля, больше силы инерции его поступательно движущейся массы.

В соответствии с этим общая сила сопротивления разгону

Величина ≈1,05 + 0,05·n_кп,

n_кп — передаточное число коробки передач, на которой производится разгон.

Мощность, которая имеется для обеспечения ускорения, представляет собой разность между мощностью, требующейся при данных условиях для преодоления сопротивления движения, и мощностью, подводимой к ведущим колесам.

Мощность, важная для перемещения автомобиля с ускорением

V — скорость автомобиля.

Из приведенной формулы видно, что чем автомобиль легче, тем большее ускорение получится развить при схожей мощности мотора.

В случае если автомобиль движется без разгона (Fp = 0 и F_и = 0), вся сила тяги тратится на преодоление сил сопротивления, и равна:

В случае, когда автомобиль замедляет ход, сила тяги становится меньше суммарной величины сил, препятствующих перемещению.

Сила тяги автомобиля.

Энергия от мотора к ведущим колесам передается через трансмиссию: сцепление, коробку передач, карданную передачу, главную передачу, дифференциал и полуоси. Благодаря наличию в трансмиссии коробки передач и главной передачи, суммарный крутящий момент М_кр на ведущих колесах автомобиля больше момента мотора М_дв.

Крутящий момент М_кр вызывает в месте контакта колеса с дорогой касательную реакцию дороги, движущую автомобиль, т. е. силу тяги. На теоретическом уровне ведущее колесо взаимодействует с дорогой в одной точке (практически же — в «пятне контакта»). Активной в этой точке является сила, с которой колесо «толкает» дорогу. Вот тут-то и появляется ответная (реактивная) сила F_T реакции дороги, которая «толкает» машину. Величина силы тяги равна отношению крутящего момента на полуосях к радиусу ведущих колес, т. е., М_кр -крутящий момент на колесе,

R — статический радиус колеса.

Таким образом, для определения силы тяги необходимо знать радиус R ведущего колеса и момент М_кр. Так как на колеса автомобиля установлены эластичные пневматические шины, то радиус колеса во время движения изменяется под влиянием действующих на колесо сил. Различают статический радиус колеса ( расстояние от поверхности дороги до оси неподвижного колеса, значение которого приводится в технической характеристике шины), динамический радиус колеса (расстояние от поверхности дороги до оси катящегося колеса) и радиус качения колеса (радиус условно недеформирующегося кольца, имеющего с данным эластичным колесом схожую угловую и линейную скорости). Для простоты расчетов силы тяги считают радиус колеса постоянным и равным статическому радиусу колеса.

Сила сцепления шины с дорогой

Сила сцепления покрышки с дорогой Р_сц.Для того чтобы автомобиль имел возможность стабильно ехать, тормозить и поворачивать, необходимо надежное сцепление покрышек с дорогой. Сила сцепления Р_сц находится в зависимости от сцепного веса автомобиля и скорости перемещения автомобиля, а также от состояния дороги и покрышек: где:

G_сц — сцепной вес автомобиля,

ᵠ_сц^— коэффициент

Коэффициент сцепления покрышек с дорогой определяет проходимость автомобиля при перемещении по влажному грунту и по скользкой дороге.

Сцепной вес автомобиля возможно, увеличить, увеличивая количество ведущих колес или смещая центр тяжести в сторону ведущего моста.

От сцепления колес с дорогой зависят максимально вероятные силы тяги и торможения, а также боковая устойчивость автомобиля.

Если сила тяги приложенная к колёсам превышает силу сцепления, то при попытке тронуться с места ведущие колеса автомобиля пробуксовывают. Если тормозная сила колеса больше силы сцепления, колесо блокируется. И в том и в ином случаях возникает юз — проскальзывание колеса относительно опоры. Юз наступает тогда, когда скорость точки касания колеса с дорогой не равна нулю относительно дороги. В случае если эта точка неподвижна относительно дороги, колесо не будет проскальзывать до тех пор, пока действующие на него в точке касания силы не превысят силы трения покоя.

Автомобиль движется благодаря наличию силы трения покоя. Ведь, если бы этого трения не было, колеса всегда проскальзывали бы относительно опоры, т. е. прокручивались бы при попытке разогнать автомобиль и блокировались бы при попытке его остановить. И если на льду колесо буксует или скользит, это означает, что соответственно силы тяги или торможения превышают силу трения (Р_сц применительно к автомобилям). Очевидно, что условием движения автомобиля без юза являются соотношения:

F_T < Р_сц— для движения под действием силы тяги;

Р_торм < Р_сц— для движения под действием тормозной силы.

При полной загрузке автомобиля положение улучшается, зато при уменьшении значения коэффициента сцепления ᵠ_сц, а оно может уменьшиться в 10 раз (например, в гололед), максимально допустимая сила тяги также уменьшается в 10 раз. Значение коэффициента сцепления зависит прежде всего от типа и состояния дороги, рисунка и степени износа протектора покрышек, давления в шинах и скорости вращения колес. При управлении автомобилем следует учитывать все эти факторы.

Торможение.

Торможение это процесс, во время которого кинетическая энергия движущегося автомобиля в результате трения преобразуется в теплоту и рассеивается в окружающем пространстве. Трение создается тормозными механизмами, установленными на каждом колесе.

Во время торможения на колесо одновременно происходят два взаимо-связанных явления: во-первых, в результате работы тормозного механизма создается тормозной момент М_т, который препятствует вращению колеса; во-вторых, в результате взаимодействия покрышки с дорогой возникает момент сцепления М_сц, стремящийся поддержать вращение колеса.

При торможении элементарные силы трения, возникающие в паре трения «колодки — тормозной барабан », создают момент трения М_т, направленный в сторону, противоположную вращению колеса, а между колесом и дорогой возникает тормозная сила Р_торм—

При полном торможении колесо блокируется и происходит рассеивание энергии в месте контакта покрышки с дорогой. В случае экстренного торможения на горизонтальной дороге, движущей силой является сила инерции автомобиля, а основной силой сопротивления движению является суммарная тормозная сила всех колес.

При рабочем торможении колесо вращается, а энергия рассеивается в тормозном механизме.

При идеальном торможении вся энергия движения автомобиля (mV²/2) превращается в тепло. Максимально возможное при торможении замедление:

g — ускорение свободного падения.

Но это лишь теоретически возможное замедление. Реально же значение замедления а меньше по многим причинам.

Во время экстренного торможения тормозной путь окажется равен:

V — скорость автомобиля, измеряемая в м/с, в момент начала торможения;

а — максимально возможное замедление автомобиля при торможении.

Формулы наглядно демонстрируют, что, если в результате изменения дорожных или погодных условий значение ᵠ_сц упало, во столько же раз снижаются максимально возможные сила торможения и замедление автомобиля.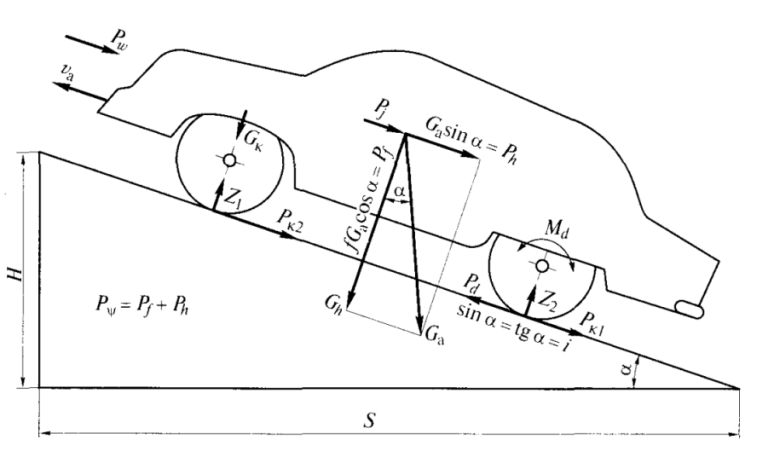

Длина тормозного пути прямопропорциональна квадрату скорости автомобиля в момент начала торможения.

Из практики известно, что юз задних колес наступает чаще юза передних так как при торможении у автомобиля опускается передняя часть.

Это объясняется тем, что при торможении автомобиля сила инерции F_H, которая приложена к ЦМ, действуя на плече Н (рис. 2, б), и тормозные силы Р_торм, лежащие в плоскости дороги, образуют относительно ЦМ тормозной момент М_торм, который вызывает перераспределение нормальных нагрузок между передним и задним мостами. При этом нагрузка на передние колеса увеличивается, а на задние уменьшается. Поэтому нормальные реакции Z_п и Z_з, действующие соответственно на передние и задние колеса автомобиля во время торможения, значительно отличаются от нагрузок G_п и G_з, которые они воспринимают в статическом состоянии

Во время резкого торможения автомобиля реакция на переднюю ось у легковых автомобилей может возрасти в 1,5 — 2 раза, а на заднюю ось уменьшиться в 0,5 — 0,7 раза.

Степень распределения суммарной нагрузки по осям при торможении зависит от высоты расположения центра масс и от расстояния между осями. С уменьшением нагрузки на заднюю ось допустимые тормозные усилия на задних колесах уменьшаются, а на передних — увеличиваются; следовательно, при торможении задние колеса более склонны к юзу.

Рис.2

Рис.2. Силы, действующие на автомобиль при торможении и остановке: ЦМ — центр масс; Н — расстояние между ЦМ и плоскостью дороги; Р_торм — тормозная сила; М_торм — тормозной момент; G — вес автомобиля;G_сц — сцепной вес автомобиля

Рис.3

Рис.3. Силы сцепления колеса с дорогой, действующие в пятне контакта колеса: F_т-сила тяги; F́_т— сила тяги при интенсивном разгоне; Р_торм -сила торможения;

Р́_торм — сила торможения при интенсивном замедлении; Р́_бок.сц. — поперечная сила сцепления при интенсивном разгоне или торможении; Р_{бок. сц.}— поперечная сила сцепления; Р_сц — сила сцепления.

В процессе торможения реакция на передние колеса увеличивается, а на задние уменьшается. Поэтому для полной реализации силы сцепления при экстренном торможении необходимо, чтобы тормозные силы были пропорциональны нормальным реакциям. Исходя из этого делают так, чтобы передние колеса тормозили настолько сильнее, насколько больше при торможении они прижимаются к дороге. Это позволяет при торможении получить наибольшую тормозную силу, поскольку сила сцепления каждого колеса пропорциональна приходящейся на него нагрузке.

Для того чтобы предотвратить блокировку задних колёс применяется регулирование давления в тормозном приводе, которое обеспечивает ограничение роста давления в тормозных механизмах задних колес при уменьшении реакции на задние колеса автомобиля. Клапан регулятора давления перекрывает подвод жидкости к тормозным механизмам задних колес в случае, когда давление в ее тормозном контуре возрастает до предельного, угрожающего блокировкой колес. Более совершенные антиблокировочные системы с электронными датчиками скорости вращения колес предотвращают блокировку колес при любых значениях коэффициента сцепления.

Заключение

В настоящей работе были рассмотрены силы, действующие на автомобиль. К ним относятся:

Сила сопротивления качению, которая всегда препятствует движению и возникает вследствие деформации шин и поверхности дороги;

Сила сопротивления подъему может быть направлена как в сторону движения, так и против него. В процессе подъема она действует в направлении, противоположном движению, и является силой сопротивления движению. При спуске эта сила, направленная в сторону движения, становится движущей;

Сила сопротивления воздуха зависит от коэффициента сопротивления воздуха, лобовой площади и скорости движения автомобиля;

Сила разгоняющая автомобиль, которая зависит от ускорения, времени и пути разгона;

Сила тяги автомобиля возникает при передачи крутящего момента с двигателя на колеса и для её определения необходимо знать радиус ведущего колеса;

Сила сцепления шины с дорогой зависит от сцепного веса автомобиля и скорости движения, она нужна для того, чтобы автомобиль мог устойчиво двигаться, тормозить и поворачивать.

Эти силы, действующие на автомобиль во время движения, влияют на изменения показателей эффективности работы автомобиля. К этим показателям можно отнести скоростные свойства автомобиля, топливная экономичность, износ деталей автомобиля, аэродинамические свойства.

Учет этих показателей позволит повысить эффективность использования автомобильного транспорта, и сократить число дорожно-транспортных происшествий.

Литература

Ваганов В.И. Вождение автотранспортных средств / Ваганов В.И., Рывкин А.А. — М.:Транспорт, 1990 – 224 с.

Горбачев М.Г. Безопасное вождение современного автомобиля / Горбачев М.Г. – м.: Рипол Классик, 2007 — 232

Калисский В.С. Автомобиль: Учебник водителя третьего класса / Калиссий В.С., Манзон А.И., Нагула Г.Е. – 5-е изд.,стереотип. – М.: Транспорт, 1980. – 368 с.

Николенко В.В. Вождение автомобиля. Практическое пособие / Николенко В.В. – 1991 — 62 с.

Тимовский А. А. Основы управления автомобилем и безопасность дорожного движения / Тимовский А.А., Нестеренко В.Б. – Арий, — 2009, 146 с.

Шухман Ю.И. Основы управления автомобилем и безопасность движения / Шухман Ю.И. – м,: ООО «Книжное издательство «За рулем», 2006.-160 с.

Интернет-источники

https://www.nkj.ru/archive/articles/9606/ (Наука и жизнь, О ТОРМОЗАХ И ТОРМОЖЕНИИ)

https://www.auto.sumy.ua/autofirm/advance/1

Силы действующие на автомобиль при движении

http://www.znaypdd.ru/forces.php

Просмотров работы: 7979

Силы, действующие на автомобиль во время его движения

Во время движения, на автомобиль действуют разные силы. Внешними силами, на преодоление которых расходуется тяговое усилие, полученное от двигателя на ведущих колесах автомобиля при его движении по горизонтальной плоскости с равномерной скоростью, являются силы сопротивления качению и сила сопротивления воздуха. При движении на подъем дополнительно надо преодолевать силу сопротивления вертикальному перемещению центра тяжести автомобиля, при ускоренном движении – силу сопротивления инерции автомобиля.

На автомобиль, как при движении, так и в неподвижном состоянии действует сила тяжести. Силой тяжести автомобиля является его масса, измеряется она в килограммах и действует параллельно по вертикали вниз, прижимая колеса к дороге (рис.1).

Рис.1. Силы, действующие на автомобиль при движении на подъем.

Сила тяжести автомобиля, стоящего неподвижно на горизонтальной плоскости, направлена вертикально вниз и распределяется по осям и колесам. Эти составляющие силы по своей величине обратно пропорциональны расстояниям между точками их приложения и точкой приложения силы тяжести автомобиля (центра тяжести). Определим центр тяжести автомобиля ЗИЛ-130. Собственная масса автомобиля ЗИЛ-130 составляет 4300 кг и распределяется по его осям: на переднюю – 2120 кг, заднюю – 2180 кг, при расстоянии между осями 3,8 м. Расстояние от центра тяжести до передней оси будет равно 2120×3,8/430 = 1,8 м, до задней оси: 2180×3,8/4300 = 2 м.

Для того чтобы узнать, как распределяется масса автомобиля на колеса, надо силу тяжести, приходящуюся на каждую ось, разделить на количество колес. Следовательно, на каждое переднее колесо будет действовать сила тяжести, равная 2120/2 = 1010 кг, на каждое заднее колесо: 2180/4 = 540,5 кг.

Как видно, колеса автомобиля могут быть прижаты к дороге с различной силой, что зависит от массы груза и его распределения в кузове. Чем ниже расположен центр тяжести, тем устойчивее автомобиль против опрокидывания. При неравномерном укладывании груза центр тяжести может сместиться вперед, назад или в сторону, при этом нарушается устойчивость и управляемость автомобиля. Положение центра тяжести некоторых автомобилей приведено в таблице:

Марка автомобиля	Высота расположения центра тяжести, мм		Расстояние от центра тяжести до передней оси, мм
	без нагрузки	с полной нагрузкой
«Москвич-412» ГАЗ-24 «Волга» ГАЗ-51А ГАЗ-53А ЗИС-130 МАЗ-500 Урал-375 ЗИЛ-157 ЗИЛ-131 КрАЗ-219 КрАЗ-222	475 615 954 820 855 1050 865 720 830 951 980	445 714 1252 1000 1200 1450 1126 1040 1165 1380 1342	1287 1380 1655 2100 1830 1860 2305 – – – –

Сила сцепления колес с дорогой возникает между ведущими колесами автомобиля и дорогой. Она равна произведению коэффициента сцепления на сцепную массу, то есть на массу автомобиля, приходящуюся на его ведущие колеса. В автомобиле со всеми ведущими осями сцепной массой является полная масса автомобиля.

Коэффициент сцепления – это отношение силы сцепления колеса с дорогой к массе, приходящейся на данное колесо, и он будет равен:

φ = Рсц / Gк,

где φ – коэффициент сцепления;
Рсц – сила сцепления колеса с дорогой;
Gк – масса, которая прижимает колесо к дороге.

Коэффициент сцепления имеет решающее значение при торможении автомобиля. Чем выше коэффициент сцепления, тем больше может быть интенсивность торможения автомобиля.

Величина коэффициента сцепления колес автомобиля с дорогой имеет существенное значение для эксплуатации транспортных средств и безопасности дорожного движения. При низком коэффициенте сцепления – в этом случае трогание автомобиля с места очень затруднено, так как оно будет сопровождаться пробуксовкой, а в свою очередь торможение – скольжением колес. В результате автомобиль не всегда удается тронуть с места, а при необходимости торможения происходят резкое значительное увеличение тормозного пути и не исключено возникновение заноса. Среднее значение коэффициента сцепления шин, имеющих неизношенный дорожный рисунок протектора, с дорогой приведено в таблице:

Покрытие дороги	Коэффициент сцепления
Покрытие дороги	на сухой поверхности	на мокрой поверхности
Цементобетон и асфальтобетон Щебеночное шоссе Каменные торцы Грунтовая дорога Утрамбованный шлак Глина Песок Уплотненный снег Обледеневая дорога Гололедица	0,7-0,8 0,6-0,7 0,5-0,6 0,5-0,6 0,5-0,6 0,4-0,5 0,2-0,3 0,2-0,3 0,12-0,15 0,08-0,10	0,3-0,4 0,3-0,4 0,3-0,35 0,2-0,4 – 0,2-0,4 0,4-0,5 – – –

Особенно сильно снижается коэффициент сцепления на дороге после первого дождя, когда образуется еще не смытая пленка жидкой грязи. Заснеженная или обледенелая дорога особенно опасна в теплую погоду, когда поверхность проезжей части подтаивает.

Повышенное давление воздуха в шинах уменьшает их опорную поверхность, вследствие чего давление возрастает настолько, что при трогании с места и при торможении сцепление колес с дорогой уменьшается.

В связи с тем, что много дорожно-транспортных происшествий происходит из-за плохого сцепления, водители при управлении автомобилем должны уметь оценивать величину коэффициента сцепления и выбирать скорость движения и приемы управления в соответствии с дорожными и погодными условиями.

Тяговая сила на ведущие колеса (Рт) расходуется на отдельные виды сопротивления движению и может быть выражена следующей формулой:

Рт = Рк + Рв ± Рп + Ри,

где Рк – сила сопротивления качения автомобиля, кг;
Рв – сила сопротивления воздуха, кг;
Рп – сила сопротивления подъему, кг;
Ри – сила инерции автомобиля, кг.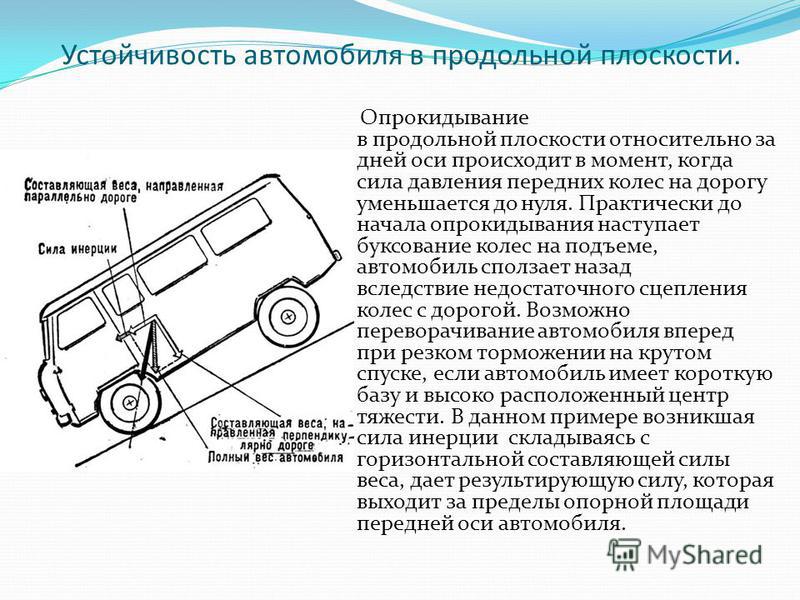

Сила сопротивления качению колес автомобиля складывается из деформации шин и грунта, трения шин о дорогу, трения в подшипниках передних колес, в рессорах и рессорных серьгах или в амортизаторах подвески автомобиля. Определение всех этих сил в различных условиях движения автомобиля очень сложно. Поэтому все эти сопротивления учитываются общим коэффициентом, установленным экспериментальным путем. Этот коэффициент называется коэффициентом сопротивления качению автомобиля.

Коэффициент сопротивления качению шин на асфальтированном покрытии равен 0,019-0,020; на гравийном покрытии – 0,02-0,025; на песке – 0,1-0,3.

Сила сопротивления воздуха слагается из любого движения встречного воздуха, разрежения за движущимся автомобилем, трения частиц воздуха о поверхность кузова автомобиля. Силу сопротивления воздуха можно определить приближенно перемножением площади проекции автомобиля на коэффициент сопротивления воздуха и скорость движения автомобиля. Коэффициент сопротивления воздуха определяется в килограммах на 1 м² площади проекции автомобиля при скорости движения 1 м/сек. Сила сопротивления воздуха зависит от величины лобовой поверхности автомобиля, его формы, а также скорости движения. С увеличением скорости автомобиля сила сопротивления воздуха возрастает пропорционально квадрату скорости движения, то есть если скорость возрастает в два раза, то сопротивление воздуха увеличивается в четыре раза.

Мощность, затрачиваемая на сопротивление воздуха, с увеличением скорости движения автомобиля возрастает пропорционально кубу скорости. Из этого следует, что груз на грузовых автомобилях надо распределять равномерно по поверхности платформы, а также не развивать высоких скоростей.

Сила, затрачиваемая автомобилем на преодоление подъема, равна массе автомобиля, умноженной на величину угла подъема.

Чем круче подъем, тем больше сила, затрачиваемая на его преодоление. При движении автомобиля под уклон, наоборот, возникает сила, способствующая ускорению движения автомобиля. При подъезде к подъему необходимо правильно оценить возможность преодоления подъема.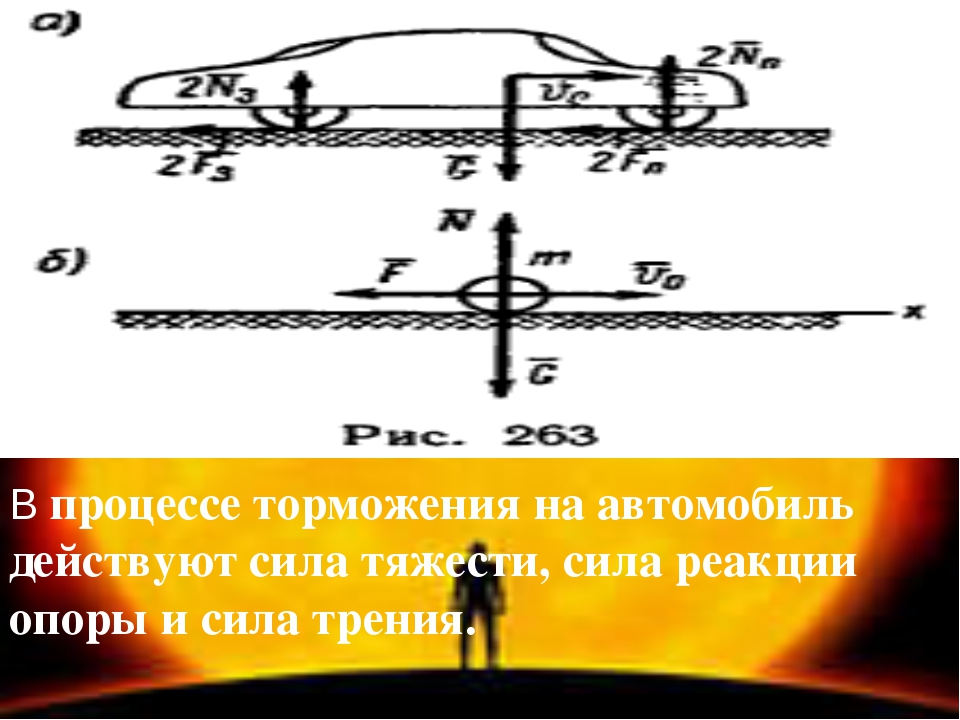 Если подъем продолжительный, его преодолевают на пониженной передаче, переключившись на нее в начале подъема. При движении автомобиля под уклон, наоборот, возникает сила, способствующая ускорению движения автомобиля. Вследствие этого на крутых спусках рекомендуется включить ту передачу, на которой можно осуществить подъем.

автомобиль, движение, дорога, колесо, коэффициент, сила, сопротивление, сцепление

Смотрите также:

7. Силы, действующие на автомобиль при прямолинейном движении.

Силы, действующие на автомобиль – внешние и массовые. Силы взаимодействия механизмов и узлов – это внутренние(не оказывают влияния на движение).

Внешние: Реакции дороги и аэродинамические реакции

Массовые(приложены к центру масс): составляющие силы тяжести, инерционная сила(разгон), центробежная(поворот), вертикальная(инерционная) сила(на вогнутых и выпуклых участках дороги).

Реакции дороги приложены к контактным поверхностям колес. Заменяют равнодействующей реакцией.

При изучении прямолинейного движения учитывают только продольные и нормальные составляющие.

Аэродинамические реакции заменяют результирующими силами P_в и P_в_Z, прилож. к ц. масс и M_в_Y

Массовые силы к центру масс.

Снаряженная(заправлен и тд) и полная(с людьми и грузом) масса авто

Вес автомобиля полной массы G_a=m_ag

К центру масс приложена также сила сопротивления подъему, поскольку она является составляющей силы тяжести:

P_п=G_asinα=G_ai α – угол продол. наклона дороги(рад), i – угол продол. наклона(%)

8. Внешняя скоростная характеристика двс. Хар. Точки, методы построения.

9. Силы сопротивления движению автомобиля(качения, подъему, дороги)

Уравнение проекций всех сил, действ. на ось X авто

Окончательное ур-ние прямолинейного движения автомобиля

Сила сопротивлению качению Рк автомобиля, движущегося по плоской поверхности, является суммой сил сопротивления качению, приложенной ко всем колесам на поверхностях их контакта с дорогой

= + = f*cosα, где f -коэффициент сопротивления качению, – вес автомобиля

Сила сопротивления подъему Pп : Рп= *sinα=*i

i=tgα – эта сила приложена к центру масс

i – уклон дороги, для спуска «+», для подъема «-»

На спуске явл-ся движущей силой(способствующей разгону)

Сила сопротивления дороги Рд – это сумма сил сопротивления качению и подъему: Рд= Рк+Рп=(f+i)+Ψ*

Ψ = f + i – суммарное дорожное сопротивление

Она определяется суммой двух Р, зависящих от рельефа и покрытия дороги

Ψ = f + i/100

10. Сила сопротивления воздуха. Коэф. Лобового сопротивления. Коэф. Обтекаемости.

Лобовая площадь.

Сила сопротивления воздуха Рв(вдоль оси х) является составляющей полной аэродинамической силы, приложенной к центру лобовой площади:

𝑃в=0,5∗ ∗𝐹∗=∗𝐹∗=

Cх – коэффициент аэродинамического сопротивления вдоль оси Х

𝜌в — плотность воздуха, F – лобовая площадь обтекания воздухом автомобиля

v – скорость обтекания воздухом автомобиля

Кв – коэффициент обтекаемости воздухом

Wв – фактор обтекаемости воздуха

Для грузовых автомобилей F=BHг, для легковых F=0,8B_гН_г

В – колея, Нг – габаритная высота, Вг –габаритня ширина авто

Скорость обтекания воздухом : 𝑉= при угле между направлением ветра и продольной осью авто

Рв – результирующая сила элементарных аэродинамических сил. Состоит из: сопротивления формы( обусловл. разностью между повышенным фронтальным и пониженным давлением позади авто)(50-60% от Рв), внутреннего сопротивления(проходящ. внутри авто потоки, охлаждение двигателя, вентиляция)(10-15% от Рв), сопротивления поверхности трения(в пограничном слое, зависит от шероховатости пов-ти)(5-10% от Рв), индуктируемое сопротивление(вызвано взаимодейств. сил, действ. в направлении продольн. оси авто, и перпендикулярное ей)(5..10% от РВ), дополнительное сопротивления(выступы)(15% от Рв)

На коэф. C_X оказывают влияние различные мелкие изменения формы автомобиля. Уменьшение C_X и лобовой площади имеет наибольшее значение для автомобилей, часто используемых при высоких скоростях движения. Заметное влияние оказывают многие геометрические параметры.

Силы, действующие на электромобиль (автомобиль)

Эта статья является первой из серии, посвященным теоретическим расчетам параметров электромобилей. Серия статей найдет свое логическое завершение в калькуляторе электромобиля, подобное уже произошло с калькулятором аккумуляторных батарей. Поскольку большинство приведенных расчетов будут справедливы и для автомобиля, и, в то же время, многие электромобили являются переделками серийных автомобилей, далее будет описана методика, справедливая также и для расчета автомобиля.

Для того, чтобы начать расчеты, надо определиться с основными силами, действующими на электромобиль. В дальнейших расчетах определимся со следующими обозначениями:

F_тяги – сила тяги на ведущих колесах
F_тр. – сила трения в трансмиссии
F_кач. – сила трения качения колес
F_под. – сила сопротивления подъему
F_возд. – сила сопротивления воздуха
F_ин. – сила сопротивления разгону (сила инерции)

Для того, чтобы электромобиль начал движение, сила тяги на ведущих колесах должна превысить сумму остальных сил – сил сопротивления движению.

Так как сила тяги на ведущих колесах может быть выражена через крутящий момент на двигателе, учитывая передаточные числа главной передачи и коробки передач, а также потери мощности в трансмиссии и радиус колес электромобиля. Можно записать следующее выражение:

F_тяги = (η_тр. * M_е * u_кп * u_гп)/r

Где:

F_тяги – сила тяги на ведущих колесах, Н
η_тр. – коэффициент потери мощности в трансмиссии электромобиля (в автомобильной трансмиссии для легкового авто η_тр.=0,9-0,92)
M_е – эффективный крутящий момент двигателя, Н*м
u_кп – передаточное число коробки передач
u_гп – передаточное число главной передачи
r – радиус ведущего колеса, м

Для расчета скорости движения электромобиля, в зависимости от частоты вращения вала двигателя, применяется следующая формула:

ν = (2*π*r*n*3,6)/(u_кп*u_гп)

Где:

ν – скорость электромобиля, км/ч
3,6 – коэффициент перевода скорости из м/с в км/ч
r – радиус ведущего колеса, м
n – частота вращения вала двигателя, Гц
u_кп – передаточное число коробки передач
u_гп – передаточное число главной передачи

Для расчета силы сопротивления качению требуется учитывать деформацию шины, деформацию дороги, силу трения шины об дорогу и силу трения в подшипниках колеса. Так как расчет влияния данных величин является достаточно сложным, на практике пользуются эмпирически полученным коэффициентом трения качения, который, в дальнейшем, участвует в расчете силы сопротивления качению.

**Таблица для определения коэффициента трения качения (взята из книги «Я строю автомобиль»)**
Дорога	Коэффициент трения качения, ƒ
Дорога	При скорости 50км/ч	Среднее значение
С асфальтобетонным или цементнобетонным покрытием в отличном состоянии	0,014	0,014-0,018
С асфальтобетонным или цементнобетонным покрытием в удовлетворительном состоянии	0,018	0,018-0,020
Булыжная мостовая	0,025	0,023-0,030
С гравийным покрытием	0,020	0,020-0,025
Грунтовая: сухая, укатанная	–	0,025-0,035
Грунтовая после дождя	–	0,050-0,150
Песок	–	0,100-0,300
Укатанный снег	–	0,070-0,100

Приведу формулу для расчета силы сопротивления качению:

F_кач. = ƒ*m*g*cosα

Где:

F_кач. – сила сопротивления качению, Н
ƒ – коэффициент трения качения
m – масса электромобиля, кг
g – ускорение свободного падения, м/с²
α – угол уклона дороги, °

При движении электромобиля (автомобиля) под уклон, на него действует сила сопротивления подъему:

F_под. = m*g*sinα

Где:

F_под. – сила сопротивления подъему, Н
m – масса электромобиля, кг
g – ускорение свободного падения, м/с²
α – угол уклона дороги, °

При движении электромобиля (автомобиля) на скоростях, превышающих скорость пешехода, заметное влияние оказывает сила сопротивления воздуха. Для расчета силы сопротивления воздуха используют следующую эмпирическую формулу:

F_возд. = C_x*S*ρ*ν²/2

Где:

F_возд. – сила сопротивления воздуха, Н
C_x – коэффициент сопротивления воздуха (коэффициент обтекаемости), Н*с²/(м*кг). C_x определяется эксперементально для каждого кузова.
ρ – плотность воздуха (1,29кг/м³ при нормальных условиях)
S – лобовая площадь электромобиля (автомобиля), м². S является площадью проекции кузова на плоскость, перпендикулярную продольной оси.
ν – скорость электромобиля (автомобиля), км/ч

Для расчета разгонных характеристик электромобиля (автомобиля) следует учитывать силу сопротивления разгону (силу инерции). Причем, нужно учитывать не только инерцию самого электромобиля, но и влияние момента инерции вращающихся масс внутри электромобиля (ротор, коробка передач, кардан, колеса). Далее приведена формула расчета силы сопротивления разгону:

F_ин. = m*a*σ_вр

Где:

F_ин. – сила сопротивления разгону, Н
m – масса электромобиля, кг
a – ускорение электромобиля, м/с²
σ_вр – коэффициент учета вращающихся масс

Приблизительно коэффициент учета вращающихся масс σ_вр можно рассчитать по формуле:

σ_вр=1,05 + 0,05*u²_кп

Где u_кп – передаточное число коробки передач

Осталось описать силу сцепления колес с дорогой. Однако, данная сила в дальнейших расчетах малоприменима, поэтому пока оставим ее на-потом.

И вот, мы уже имеем представление об основных силах, действующих на электромобиль (автомобиль). Знание этого теоретического вопроса вскоре сподвигнет нас на изучение следующего вопроса – вопроса расчета характеристик электромобиля, необходимых для обоснованного выбора двигателя, аккумуляторной батареи и контроллера.

Специальные термины и обозначения для ходовой части автомобиля Volkswagen

Современные автомобили имеют всё более сложные и качественные шасси, которые должны соответствовать как требованиям по комфортабельности и спортивности, так и, в особой степени, требованиям безопасности движения.

Для того, чтобы требования к ходовой части выполнялись в течение всей «жизни автомобиля», а также после возможных аварий, сегодня существуют отличные возможности по проверке геометрии ходовой части и корректировке неправильных настроек.

Ходовая часть является связующим звеном между автомобилем и дорожным полотном. Как силы, действующие на опорную поверхность колеса и силы тяги, так и возникающие при прохождении поворотов силы бокового увода передаются ходовой частью на дорогу через колёса автомобиля.

Ходовая часть подвергается воздействию множества сил и моментов. Увеличивающаяся мощность автомобилей, а также возросшие требования к их комфортабельности и безопасности ведут к постоянному росту требований к ходовой части.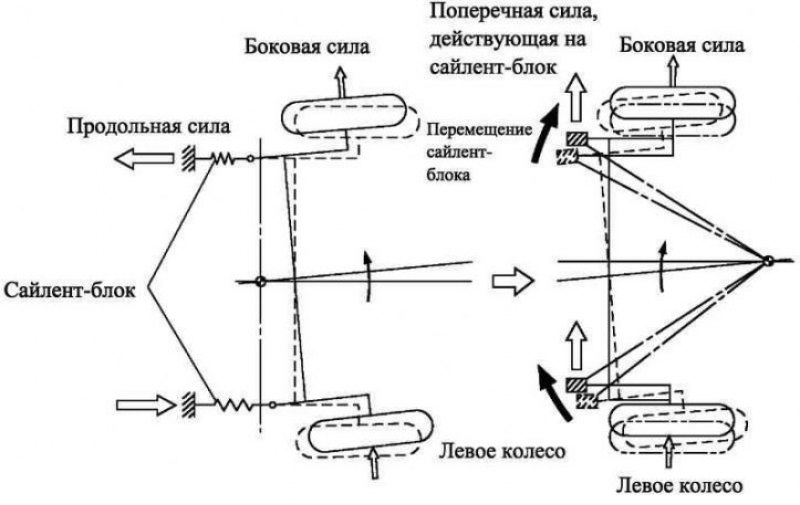

По мере усложнения конструктивного исполнения кинематики ходовой части с течением времени трудоёмкость регулировки постоянно увеличивалась, а допуски при регулировке постоянно уменьшались.

Для проверки и, при необходимости, регулировки кинематики ходовой части необходимо проверить или отрегулировать ходовую часть на специальных измерительных стендах. При этом необходимо учитывать, что регулировать ходовую часть следует только после проведённого ремонта, или возникновения проблем в этой ходовой части.

К ходовой части автомобиля относятся:

подвеска колёс,

колёса,

пружины,

амортизаторы,

передняя/задняя подвески,

рулевое управление,

тормоза, включая элементы управления,

подрамник.

Точка опоры колеса — это расположенная в средней плоскости колеса точка пересечения перпендикуляра, проходящего через ось вращения колеса, с плоскостью дорожного полотна.

Средняя плоскость колеса проходит перпендикулярно оси вращения колеса по центру шины колеса.

Колёсная база — это расстояние между центрами колёс передней и задней оси.

Ширина колеи — это расстояние между серединами шин колёс каждой оси.

В случае независимой подвески колёс с поперечными или диагональными рычагами при сжатии и отбое упругих элементов подвески ширина колеи меняется.

Геометрическая ось движения представляет собой биссектрису суммарного угла схождения колёс задней оси.

Задняя ось является осью, определяющей курсовое направление автомобиля. Поэтому все измерения для колёс передней оси, а также некоторых вспомогательных систем водителя выполняются относительно геометрической оси движения. В оптимальном состоянии геометрическая ось движения лежит в продольной средней плоскости автомобиля.

Продольная средняя плоскость автомобиля представляет собой рассекающую автомобиль неподвижную плоскость, перпендикулярную дорожному полотну и проходящую через середину колеи передних и задних колёс (плоскость X-Z).

Угол тяги представляет собой угол между продольной средней плоскостью автомобиля (2) и геометрической осью движения (1). Он образуется из геометрической оси движения, бокового смещения и перекоса задней подвески. Если биссектриса угла направлена влево вперёд, то угол тяги называется положительным. Если она направлена вправо вперёд, то угол называется отрицательным.

Положение прямолинейного движения. Это положение колёс является вспомогательным положением, при котором индивидуальные углы схождения колёс относительно продольной средней плоскости у обоих передних колёс одинаковые. В этом положении осуществляется измерение углов установки колёс задней оси.

Оптимальный угол тяги. Индивидуальный угол схождения колёс задней оси представляет собой угол между продольной средней плоскостью автомобиля и секущей средней плоскости отдельного колеса.

Угол тяги положительный (положительное схождение), когда передняя часть колеса обращена в сторону продольной средней плоскости автомобиля. Угол тяги отрицательный (отрицательное схождение), когда передняя часть колеса обращена в сторону от продольной средней плоскости автомобиля.

Суммарное схождение получают путём сложения индивидуальных углов схождения левого и правого колёс одной оси, причём необходимо учитывать знаки значений индивидуальных углов схождения.

Индивидуальный угол схождения колёс передней оси представляет собой угол между геометрической осью движения и секущей средней плоскости отдельного колеса.

Отрицательное схождение. Он положительный (положительное схождение), когда передняя часть колеса обращена в сторону геометрической оси движения. Он отрицательный (отрицательное схождение), когда передняя часть колеса обращена в сторону от геометрической оси движения.

Развал — это угол между средней плоскостью колеса и вертикалью к точке пересечения средней плоскости колеса с опорной поверхностью. Различают положительный и отрицательный развал:

положительный (+) — когда верхняя часть колеса наклонена от средней плоскости колеса наружу;

отрицательный (–) — когда верхняя часть колеса наклонена от средней плоскости колеса внутрь.

Поперечный наклон оси поворота — это наклон оси поворота (b) относительно перпендикуляра (a) (в плоскости, параллельной продольной средней плоскости автомобиля) к дорожному полотну. Благодаря поперечному наклону оси поворота при повороте управляемых колёс кузов автомобиля приподнимается, вследствие чего возникают силы, стремящиеся вернуть колесо в прямолинейное положение.

Различают положительное (+), отрицательное (–) и нулевое плечо обкатки. Плечо обкатки определяется развалом, поперечным наклоном оси поворота и вылетом колёсного диска.

Плечо обкатки — это расстояние между точкой опоры колеса и точкой пересечения продолжения оси поворота колеса (называемой также осью поворота) с опорной поверхностью колеса.

Плечо обкатки — динамическая стабилизация автомобиля. При отрицательном плече обкатки колесо с большим коэффициентом сцепления сильнее отклоняется внутрь — колесо самостоятельно стремится повернуться в сторону, противоположную развороту, — водитель должен просто удерживать рулевое колесо. При нулевом плече обкатки предупреждается передача посторонних сил на рулевое управление при подтормаживании тормозов с одной стороны автомобиля и при повреждении шины.

Продольный наклон оси поворота (кастер). Продольный наклон оси поворота — это наклон оси поворота в направлении продольной оси автомобиля относительно вертикали к плоскости дорожного полотна.

Различают положительный и отрицательный угол продольного наклона оси поворота:

положительный — «точка опоры колеса следует за точкой пересечения оси поворота колеса с опорной поверхностью» — колёса стремятся к положению прямолинейного движения => динамическая стабилизация;

отрицательный — «точка опоры колеса опережает точку пересечения оси поворота колеса с опорной поверхностью» — колёса волочатся.

Обратное схождение в повороте представляет собой разницу углов поворота колеса, движущегося по внешнему радиусу поворота (меньший угол) и колеса, движущегося по внутреннему радиусу поворота (больший угол).

Обратное схождение в повороте задаётся рулевой трапецией. Таким образом оно даёт представление о принципе работы рулевой трапеции при соответствующем повороте управляемых колёс — влево или вправо.

Передняя подвеска, рычаги рулевых тяг и рулевой механизм с рулевыми тягами в совокупности образуют рулевую трапецию. С помощью рулевой трапеции обеспечиваются разные углы поворота управляемых колёс, необходимые для движения в поворотах. Поворотный кулак и рычаги рулевой тяги расположены относительно друг друга не под углом 90°. Из этого вытекают неравные расстояния перемещения концов обоих рычагов рулевой тяги при повороте управляемых колёс. Это приводит к повороту управляемых колёс на разные углы.

Максимальный угол поворота — это угол средней плоскости колеса, движущегося по внутреннему радиусу поворота (B), и колеса, движущегося по внешнему радиусу поворота (A) относительно продольной средней плоскости автомобиля при повороте рулевого колеса влево-вправо до упора.

Максимальные углы поворота в обе стороны должны быть одинаковыми. Это обеспечивает одинаковые диаметры разворота.

Угол бокового увода колеса — это угол, образуемый плоскостью колеса к направлению движения (направлению движения колеса). Угол бокового увода возникает в том случае, когда на катящийся автомобиль действуют посторонние боковые силы, такие, как сила ветра и центробежная сила. При этом колёса меняют направление своего движения и движутся под определённым углом к прежнему направлению движения.

Если угол бокового увода передних и задних колёс одинаков, автомобиль обладает нейтральной поворачиваемостью. Если угол бокового увода передних колёс больше, возникает недостаточная поворачиваемость. Если угол бокового увода больше у задних колёс, возникает избыточная поворачиваемость.

Угол бокового увода зависит от нагрузки на колесо, посторонней силы, конструкции шины, профиля шины, давления воздуха в шине и силы трения сцепления.

Угол смещения колеса представляет собой угол между линией, соединяющей точки опоры колёс, и линией, проходящей под углом 90° к геометрической оси движения. Различают положительный и отрицательный угол смещения колеса:

положительный — правое колесо смещено вперёд;

отрицательный — правое колесо смещено назад.

Разница колёсной базы — это угол между соединительными линиями точек опоры передних и задних колёс. Различают положительный и отрицательный угол:

положительный — колёсная база с правой стороны автомобиля больше колёсной базы с левой стороны;

отрицательный — колёсная база с правой стороны автомобиля меньше колёсной базы с левой стороны.

Боковое смещение — это угол между линией, соединяющей точки опоры переднего левого (правого) и заднего левого (правого) колёс и геометрической осью движения. Боковое смещение позволяет сделать вывод о возможных повреждениях кузова.

Разница ширины колеи представляет собой угол между линией, соединяющей точки опоры левого переднего и левого заднего колёс и линией, соединяющей точки опоры правого переднего и правого заднего колёс. Разница ширины колеи определяется как положительная, когда ширина колеи задних колёс больше ширины колеи передних колёс.

Смещение оси считается положительным, когда задняя ось, соотнесённая с геометрической осью движения, смещена относительно передней оси вправо. Смещение оси позволяет сделать вывод о возможных повреждениях кузова.

Вылет колёсного диска — это расстояние от середины обода до внутренней плоскости прилегания колёсного диска к ступице («x»).

Вылет колёсного диска влияет на ширину колеи и плечо обкатки. Различают три варианта вылета колёсного диска:

нулевой — когда внутренняя плоскость прилегания расположена точно посередине колеса;

положительный — когда внутренняя плоскость прилегания смещена к внешней стороне колеса относительно середины колеса — уменьшение ширины колеи;

отрицательный — когда внутренняя плоскость прилегания смещена к внутренней стороне колеса относительно середины колеса — увеличение ширины колеи.

Расчётное положение

При разработке автомобиля вначале определяется расчётное положение. Это положение описывается системой осей координат X-Y-Z.

При этом оси Z и X проходят через центр передней подвески, ось Y в большинстве случаев проходит точно через центры передних колёс. Расчётное положение соответствует положению автомобиля при номинальной установочной высоте расположения кузова.

Все номинальные значения, указанные производителем автомобиля, относятся к расчётному положению.

Таким образом, при определении и сравнении данных в процессе проверки углов установки колёс всегда учитывается расчётное положение — это касается и описываемых далее терминов и обозначений для ходовой части.

Установочная высота

Установочная высота, или высота уровня оказывает решающее влияние на результаты проверки углов
установки колёс. На неё влияет загрузка, степень заправки топливного бака или других ёмкостей с жидкостью,
а также перепад температур, вследствие чего могут изменяться такие параметры ходовой части, как развал,
схождение и угол продольного наклона оси поворота управляемых колёс.

Полная информация в .pdf доступна здесь.

Автоцентр Сити — Каширка Volkswagen

Москва, Внешняя сторона МКАД, 23 км

ежедневно: 08:00-21:00

Программа помощи на дорогах «Гарантия Мобильности» от Volkswagen в России

В случае если вы не можете устранить неисправность самостоятельно, в том числе следуя инструкциям, полученным при технической консультации по телефону круглосуточной помощи, к вам будет отправлена мобильная группа для оказания технической помощи.
Мобильная техническая группа выезжает круглосуточно, включая выходные и государственные праздничные дни. Для удобства проводится СМС-информирование о статусе процесса оказания технической помощи*.

Ориентировочные сроки** прибытия мобильной группы с момента звонка по телефону круглосуточной помощи 8-800-700-70-11:

В пределах города
(для Москвы — в пределах МКАД)
до 60 минут**
До 100 км от административных границ города
(для Москвы — от границ МКАД)
до 2 часов**
До 200 км от административных границ города
(для Москвы — от границ МКАД)
до 3 часов**
До 300 км от административных границ города
(для Москвы — от границ МКАД)
до 5 часов**

Примеры услуг, оказываемых мобильной группой:

Подзарядка аккумулятора на месте, запуск двигателя.
Вскрытие автомобиля (например, если вы потеряли ключи или случайно закрыли их в автомобиле или если на морозе замёрзли замки).
Замена колеса после прокола или повреждения шины на запасное колесо (при его наличии) или доставка колеса в шиномонтаж и обратно (при отсутствии колеса; при этом стоимость работ по ремонту шины/колеса или приобретение шины/колеса вы оплачиваете отдельно).
Подвоз топлива в количестве, необходимом для того, чтобы доехать до ближайшей АЗС (максимальное количество — 10 литров), стоимость топлива оплачивается отдельно.

_{*Устранение неисправности на месте и эвакуация автомобиля не производятся в следующих случаях: если работы имеют характер регламентных, связанных с регулярным ТО (например, замена тормозных колодок, масла, технических жидкостей и пр.), если клиент находится в состоянии алкогольного или наркотического опьянения.
**Срок прибытия мобильной группы может быть увеличен с учётом пробок.}

2} {r} $$

Если вы увеличиваете скорость, горизонтальная составляющая нормальной силы должна увеличиваться, чтобы машина продолжала совершать круговое движение. Это условие, наложенное дорогой. Но, Нормальная сила всегда перпендикулярна поверхности. Итак, $ N_ \ mathrm {vertical} $ также должно увеличиваться таким образом, что если угол наклона (не показан на рисунке) равен $ \ theta $,

$$ \ cot \ theta = \ frac {N_ \ mathrm {vertical}} {N_ \ mathrm {horizontal}} $$

Поскольку $ \ cot \ theta $ постоянна, вертикальная сила должна увеличиваться пропорционально увеличению горизонтальной силы.

$ {N_ \ mathrm {vertical}} $ — это сила, которая заставляет машину двигаться вверх.

РЕДАКТИРОВАТЬ: $ —

На поверхности дороги нет составляющей нормальной силы. $ N_ \ mathrm {horizontal} $ и $ N_ \ mathrm {vertical} $ являются компонентами $ N $. Вы не можете взять компонент векторной составляющей. См. «Компонент компонента вектора».

Нельзя увеличить скорость «Автомобиля» нажатием на педаль газа. Чтобы увеличить его скорость, вы должны либо поставить уже движущуюся машину с необходимой скоростью, либо прикрепить что-то вроде вентилятора или ракетного ускорителя позади машины, чтобы увеличить ее скорость.

Трасса или дорога круговая. Итак, как только вы увеличиваете скорость автомобиля с помощью какого-либо механизма, передняя часть колес или автомобиль ударится с большей силой о изогнутую поверхность, что приведет к большей нормальной силе (помните, что скорость автомобиля на дорога без трения не связана с угловой скоростью колес.)

Кажущаяся радиально наружу сила — это сила, прикладываемая для увеличения скорости автомобиля. Смотрите изображение

Если сила приложена к $ \ mathrm {A} $, приближаясь к $ \ mathrm {B} $, сила будет иметь компонент вдоль $ \ mathrm {OB} $.Это увеличит нормальную силу, которая, в свою очередь, подтолкнет автомобиль вверх. $ \ mathrm {O} $ — это центр круга дороги с насыпью (извините, я не смог включить это в рисунок).

ДИНАМИКА АВТОМОБИЛЯ

Динамика автомобиля — сложный аналитический и экспериментальная технология, которая используется для изучения и понимания откликов автомобиль в различных ситуациях движения. В сфере обучения водителей нет необходимости иметь дело с особенности этой технологии, а скорее с некоторыми из основных физических принципы, вовлеченные в это.В В этом модуле будут обсуждаться следующие принципы.

И. Кинетическая энергия

II. Центробежная сила

III. Инерция

IV. Трение

В. Тяга

Есть не имеет намерения дать полное техническое определение каждого принципа, но представьте их так, чтобы было полезно понять, почему автомобиль действует так, как это делает.

Кинетическая энергия — это термин, описывающий энергию a автомобиль имеет благодаря своей массе и скорости. Его формула проста, но говорит о многом.

Кинетическая энергия = (масса) x (скорость) ²

Это показывает, что кинетическая энергия транспортного средства увеличивается как квадрат скорости. Это означает, что при удвоении скорости энергия увеличивается в четыре раза. раз.Это увеличение энергии не вызывает проблема, если ее не нужно быстро рассеять или перенаправить.

Один способ, которым кинетическая энергия может рассеиваться очень быстро, — это когда автомобиль сталкивается с твердый объект. В этом случае, когда скорость увеличивается вдвое, в четыре раза больше энергии, доступной для повреждения транспортного средства и травмировать пассажиров. Кинетический Энергия автомобиля весом 4000 фунтов, движущегося со скоростью 100 миль в час, равна 1,36 миллиона фут-фунтов достаточно, чтобы поднять мужчину весом 175 фунтов 1.5 миль. Чтобы остановить этот автомобиль, необходима огромная энергия. рассеиваться. Это можно сделать ударом или тормозами. Остановка расстояние связано с квадратом скорости; следовательно, для скорости 30 миль в час требуется четыре умноженное на расстояние до остановки, превышающее 15 миль в час. Многие водители никогда не задумываются о последствиях увеличения скорости, но они должны осознавать связанные с этим риски.

ЦЕНТРОБЕЖНАЯ СИЛА

Когда автомобиль поворачивается, центробежная сила действует на автомобиль и пытается толкнуть его вне кривой.Формула это:

Центробежная сила = (масса) X (скорость) ² / радиус поворота

Это показывает, что центробежная сила увеличивается как квадрат скорости. Также при заданной скорости малый (узкий) радиус повороты производят больше силы, чем повороты с большим радиусом. Большое количество центробежной силы требует одинаково больших количеств противодействующей силы от шин, если автомобиль должен оставаться на Дорога.Шины можно рассматривать как струны от каждого конца транспортного средства к центру поворота. Если центробежная сила выше, чем шины могут противодействовать, одна или обе струны порвутся. После этого автомобиль покинет поворот.

ИНЕРЦИЯ

Инерция сопротивление изменению направления или скорости тела в состоянии покоя. или в движении. В данном случае это связанные с изменением курса или направления транспортного средства; то есть изменение от движения прямо до поворота.

важность инерции и распределения веса, поскольку они связаны с вождением, заключается в том, что они влияют на количество времени, необходимое для перехода от прямого к поворот или наоборот. Хотя эти изменения при обычной загрузке транспортного средства невелики, водителю следует распознавать необычную загрузку транспортного средства, например, размещение большого груза на задней двери универсала (или добавление тяжелого груза на крыша транспортного средства) вызовет изменения в способе движения транспортного средства и регулировки должно производиться в управлении автомобилем соответственно.

С инерция диктует, что движущееся тело будет продолжать движение по прямой линии, необходимо приложить силу, чтобы заставить автомобиль повернуть. Эта сила называется Центростремительная сила , и возникает в результате растяжения шин при движении автомобиля с прямой дороги. Центробежная сила должна превышать центробежную. усилие для поворота автомобиля.

МОМЕНТЫ ИНЕРЦИИ:

А. Шаг силы, ощущаемой при ускорении или торможении, вокруг (Горизонтальная ось) автомобиля

Б. Сила ощущается при повороте, движение из стороны в сторону (Боковое ось) автомобиля

С. Рыскание сила, ощущаемая при вращении вокруг (вертикальная ось) автомобиль

ПОЛЯРНЫЙ МОМЕНТ ИНЕРЦИИ

Очень важная концепция обращения, которая диктует готовность автомобиля изменить направление движения, если это называется полярным моментом. инерции.Полюса инерции просто другой способ сказать центр концентрации веса. Момент в этой концепции определяется расположением центра тяжести спереди назад. Автомобиль поворачивает (меняет направление) вокруг своего центр тяжести в углу, поэтому чем дальше центры тяжести концентрации расположены от центра тяжести (что является их общим центр), тем больше момент.

Высокий полярный момент инерции присутствует, когда весовые концентрации велики и далеко друг от друга.Низкий полярный момент инерции обнаруживается, когда вес концентрации невелики и близки друг к другу. Другими словами, легче управлять транспортным средством с низкой полярностью. момент инерции.

Автомобиль с низким полярным моментом инерции дает быстрое реагирование на команды рулевого управления. А автомобиль с высоким полярным моментом имеет высокую курсовую устойчивость (т.е. сопротивляется изменению своего направления).

Трение определяется как сопротивление движению между двумя поверхностями.Есть четыре основных типа трения.

А. Статическая удерживающая сила между двумя неподвижными поверхностями

Б. Скольжение сопротивления движению между двумя поверхностями, которые перемещаются друг через друга

С. Rolling Сопротивление движению катящегося объекта, как мяча, цилиндр или колесо

Д. Внутреннее сопротивление движению в упругих объектах (шины получают нагреваются от внутреннего трения при изгибе)

величина трения между двумя поверхностями зависит от:

1) вещество материала

2) Шероховатость поверхностей

3) величина силы, прижимающей поверхности друг к другу

4) наличие смазочных материалов

величина трения между двумя поверхностями называется коэффициентом трения .

КОЭФФИЦИЕНТ ТРЕНИЯ

Термин «коэффициент трения» определяется как максимальная сила, которую может создать шина на заданном дорожном покрытии состояние, разделенное на вес шины. Его формула:

Максимально возможное усилие

Коэффициент трения = вес шины

ИЛИ

Максимальное доступное усилие = коэффициент трения X Вес нагрузки на колесо

Таким образом, маневренность автомобиля на сухой Дорога зависит в первую очередь от дорожного покрытия и веса транспортного средства.На мокрой дороге другие факторы, например, шина состояние также необходимо учитывать.

По мере ускорения или замедления автомобиля больше быстро, или когда автомобиль поворачивает на более высоких скоростях, он требует большего тяговые силы от автопоезда. Комбинация шины и дороги будет создавать эти силы вплоть до предел трения.

Тяга определяется как сцепление шины с поверхностью дороги.Силы тяги три:

1) Привод тяги Для ускорения автомобиля

2) Тормозная тяга Для замедления или остановки автомобиля

3) Тяга на повороте Поворот автомобиля

при каждый раз, когда сила тяги становится больше, чем коэффициент трения, автомобиль выйдет из-под контроля.

А водитель может задействовать три силы. Для любой ситуации существует определенный уровень трения. (коэффициент) для приложения этих сил и, следовательно, для маневрирования автомобиль. Когда водитель напрягает либо тормозная сила, либо сила ускорения при одновременном приложении силу поворота, вы должны добавить силы, учитывая доступные трение. Другими словами, сумма тяга при вождении или торможении и тяга на поворотах не должны на превышать предел трения, иначе автомобиль выйдет из-под контроля.По возможности избегайте торможения или ускоряется при прохождении поворотов. Этот позволяет использовать все имеющееся трение при прохождении поворотов.

А вращающаяся шина не может обеспечить полное сцепление с дорогой при ускорении. Если водитель вызывает пробуксовку ведущего колеса при при прохождении поворотов автомобиль может выйти из-под контроля.

А заблокированная шина обеспечивает сцепление на поворотах без и пониженное торможение тяга. Когда водитель блокирует колеса в повороте, не будет реагировать на рулевое управление .При торможении максимальный коэффициент трение; следовательно, максимальная тормозная способность — это когда водитель применяет тормоза на уровне 15% пробуксовки.

GCSE Forces | Пересмотрите трение и сопротивление при торможении

В этом тесте по физике GCSE рассматриваются силы и торможение. Понимание тормозных сил — важная часть умения управлять автомобилем. Знание примерно того, сколько вам потребуется до остановки, важно не только для вас, но и для безопасности других участников дорожного движения.

Прежде чем мы рассмотрим тормозную силу, действующую на транспортное средство, необходимо понять, какие силы действуют на транспортное средство. Движущая сила исходит от двигателя, и он движется вперед. Вес создается силой тяжести, действующей на массу транспортного средства, удерживая его на земле. Сила противодействия действует в направлении, противоположном весу. Противодействуют движущей силе две силы: трение с дорогой и сопротивление воздуха. Сопротивление воздуха намного больше, чем трение о дорогу, когда автомобиль находится в движении.

Когда автомобиль находится в состоянии покоя, все силы, действующие на него, уравновешиваются. Когда водитель запускает двигатель и включает передачи, движущая сила передается на ведущие колеса. Силы теперь неуравновешены, и автомобиль движется вперед (или назад, если, конечно, включена задняя передача !!). После этого автомобиль разгонится. По мере того, как транспортное средство набирает скорость, сопротивление воздуха увеличивается, и когда оно становится той же величины, что и движущая сила, транспортное средство больше не будет ускоряться, поскольку силы снова уравновешиваются.Если водитель снимает ногу с педали акселератора, движущая сила уменьшается, и автомобиль замедляется, пока не наступит момент, когда сопротивление воздуха снова уравновесит движущую силу.

Полагаться на сопротивление воздуха для замедления транспортного средства можно только в том случае, если вы хотите контролировать скорость медленно, поэтому автомобили оснащены тормозными системами. Тормозная сила действует против движущей силы и сама по себе намного превышает сопротивление воздуха, а это означает, что водитель может остановить свой автомобиль намного быстрее.

Расстояние, необходимое для остановки автомобиля или любого другого транспортного средства, зависит от двух факторов — расстояния, на которое способен мыслить водитель, и тормозного пути. И то, и другое зависит от скорости движения автомобиля. Если транспортное средство движется с низкой скоростью, обе они короче, но они значительно увеличиваются, если транспортное средство движется с большей скоростью.

Водителю требуется всего доли секунды, чтобы отреагировать на ситуацию и задействовать тормоза, но в течение этого периода времени транспортное средство все еще движется со скоростью.Чем быстрее он движется, тем дальше он проедет — это называется «дистанцией размышлений», и для каждого водителя оно разное. Для отдельного водителя на определенной скорости время реакции и, следовательно, расстояние мышления увеличивается с усталостью, если он употреблял алкогольные напитки, принимал наркотики или отвлекался, например, слушая громкую музыку или разговаривая по мобильному телефону.

После того, как водитель отреагировал и нажал на педаль тормоза, расстояние, необходимое для его остановки, зависит не только от скорости транспортного средства, но и от того, насколько сильно тормоза задействованы, состояния тормозов, состояния шин. , погодные условия и состояние дорожного покрытия.

Глава 4 Концепции

Глава 4

Концептуальные вопросы: 5, 6, 10, 24

| ВЕРНУТЬСЯ К ДОМАШНЕМУ ЗАДАНИЮ |

5. Пытаясь затянуть ослабленную стальную головку молотка, плотник держит молоток вертикально, поднимает его, а затем быстро опускает, ударяя нижним концом деревянной ручки о доску. Объясните, как это прижимает голову к ручке.

Пока рукоятка и головка молотка движутся вниз, они оба имеют движение. Это кажется очевидным и избыточным заявлением, но это важная часть этой головоломки. Сила прилагается к рукоятке (доской), поэтому она ускоряется до остановки, но головка молота все еще движется. Он продолжает двигаться, пока ручка не ускоряет его до остановки, что происходит только при движении головки вниз.

6. Какая сила заставляет автомобиль двигаться вперед? Помните, что это должна быть внешняя сила , сила — все внутренние силы складываются в ноль.Как двигатель способствует движущей силе?

Чтобы что-то разогнать, нужна сила извне. Единственное, что действует на машину, ускоряющуюся из состояния покоя, в прямом направлении — это трение о землю. Это кажется обратным — как трение может вызвать движение , если оно всегда действует против движения вещей? Хитрость здесь в том, что шина отталкивается от дороги, поэтому дорога должна автоматически подталкивать шину вперед.Это 3-й закон Ньютона. Подумав об этом, вы увидите множество примеров того, как трение толкает предметы вперед, когда они толкаются назад: ходьба, выталкивание себя из кровати, толкание велосипеда вперед и т. Д.

Ой, двигатель. Все, что делает двигатель, — это заставляет штуковину двигаться, заставляя вращаться шестеренку, заставляя вращаться ось, заставляя вращаться шину. Итак, внутри машины действует множество других сил. Но сила, непосредственно ответственная за ускорение автомобиля, — это трение дороги.

Итак, что делать, когда машина останавливается?

10. Грузовой поезд состоит из паровоза и нескольких одинаковых вагонов на ровной поверхности. Определите, является ли каждое из этих утверждений правильным или неправильным, и объясните, почему:

а. Если поезд движется с постоянной скоростью, двигатель должен тянуть с силой, превышающей вес поезда.
Это ЛОЖЬ. Если поезд движется с постоянной скоростью, он должен тянуть в прямом направлении с некоторой силой, достаточной только для уравновешивания сил, тянущих в противоположном направлении, таких как трение.Его не нужно сравнивать с весом поезда, и ему не нужно тянуть сильнее, чем какая-либо конкретная сила, потому что он не ускоряется.

г. Если поезд движется с постоянной скоростью, тяговое усилие двигателя на первом вагоне должно превышать td обратное усилие этого вагона на двигателе.
ЛОЖНЫЙ. Не требуется, чтобы тяга вперед на превышала силы, тянущей назад. Он должен балансировать только с силой, чтобы получить нулевую чистую силу и нулевое ускорение.

г. Если поезд движется накатом, его инерция заставляет его замедляться и в конечном итоге останавливаться.
ЛОЖНЫЙ. «Инерция» ничего не делает — это не сила. Это просто свойство объектов оставаться в движении, что они и делают все, и бывает труднее изменить движение, когда объект имеет большую массу (часто это считается способом количественной оценки инерции). Если когда-либо происходит толчок, притяжение и т. Д., Это должно быть вызвано внешней силой к объекту. В этом случае это, вероятно, трение, но это также может быть сила тяжести, тянущая вниз с холма, сопротивление воздуха и т. Д.

24. Вы решили проверить свои знания физики во время перелета через водопад в бочке. Вы берете с собой бейсбольный мяч в бочку и, падая вертикально вниз, отпускаете мяч. Что вы ожидаете увидеть при движении шара относительно ствола? . . .

Ясно, что это вопрос с подвохом. Вы ничего не увидите, потому что внутри бочки темно !!

Но, если бы вы, , могли видеть внутри бочки, вы бы воссоздали сценарий, который мы разыгрываем в задаче с лифтом в классе.Во-первых, вы знаете, что все объекты падают с постоянной скоростью ускорения -g . Итак, вы идете вперед и вытаскиваете лист бумаги, пока падаете в ba

SPASH!

Ой, слишком поздно. Но предположим, что вы выполнили расчет до того, как попали в ствол, что всегда является хорошей идеей. Вы заметите, что сила, действующая на бейсбольный мяч — это его вес ( мг, ) и ваша рука, толкающая вверх. Как мы уже упоминали, ускорение мяча составляет -g .Итак, когда вы дойдете до линии:

N — мг = m (-g)

и решите для Н , вы получите результат, что эта сила контакта равна нулю! Это означает, что вам не нужно удерживать мяч, он просто парит там!

Другой способ представить это — знать, что все объекты падают с одинаковой скоростью, включая бочку, вас и ваш бейсбольный мяч. Если вы все падаете одинаково, никто из вас ничего не догонит, поэтому ничто не будет давить ни на что другое.

Но почему это это? Почему все падает с одинаковой скоростью? И почему такая скорость разгона -g? Итак, теперь, когда вы знаете кое-что о гравитации, составьте уравнение, в котором результирующая сила, действующая на объект, является результатом гравитационной силы здесь, на Земле, F = GMm / r ² (где «M» — масса Земли а «m» — это масса вас или любого другого объекта, притягиваемого Землей). Это должно быть равно вашей массе, умноженной на ускорение, или мА . Когда вы настраиваете это, вы замечаете, что м с каждой стороны компенсируются, и у вас есть уравнение для ускорения.Угадайте, чему равно это ускорение, если вы введете правильные значения G, M и r? И тот факт, что m компенсирует, означает, что это ускорение , а не , зависит от массы падающего объекта. Это то, что открыл Галилей, и это то, что мы использовали в нескольких главах. Это объясняет, почему это работает.

| ВЕРНУТЬСЯ К ДОМАШНЕМУ ЗАДАНИЮ |

5.3 Второй закон Ньютона | University Physics Volume 1

Второй закон Ньютона тесно связан с его первым законом.Он математически показывает причинно-следственную связь между силой и изменениями в движении. Второй закон Ньютона является количественным и широко используется для расчета того, что происходит в ситуациях с применением силы. Прежде чем мы сможем записать второй закон Ньютона в виде простого уравнения, которое дает точное соотношение силы, массы и ускорения, нам нужно отточить некоторые идеи, о которых мы упоминали ранее.

Сила и ускорение

Во-первых, что мы подразумеваем под изменением движения? Ответ заключается в том, что изменение движения эквивалентно изменению скорости.Изменение скорости по определению означает ускорение. Первый закон Ньютона гласит, что чистая внешняя сила вызывает изменение движения; таким образом, мы видим, что чистая внешняя сила вызывает ненулевое ускорение .

В разделе «Силы» мы определили внешнюю силу как силу, действующую на объект или систему, которая возникает вне объекта или системы. Давайте рассмотрим эту концепцию дальше. Интуитивное представление о внешних верно — это вне интересующей нас системы. Например, на (Рисунок) (а) интересующая система — это автомобиль плюс человек в нем.Две силы, проявленные двумя учениками, — это внешние силы. Напротив, между элементами системы действует внутренняя сила. Таким образом, сила, с которой человек в автомобиле держится за рулевое колесо, представляет собой внутреннюю силу между элементами интересующей системы. Согласно первому закону Ньютона, только внешние силы влияют на движение системы. (Внутренние силы нейтрализуют друг друга, как объясняется в следующем разделе.) Следовательно, мы должны определить границы системы, прежде чем мы сможем определить, какие силы являются внешними.Иногда система очевидна, тогда как в других случаях определение границ системы более тонкое. Концепция системы является фундаментальной для многих областей физики, как и правильное применение законов Ньютона. Эта концепция многократно пересматривается при изучении физики.

Рисунок 5.10 Различные силы, действующие на одну и ту же массу, вызывают разное ускорение. (а) Два студента толкают заглохшую машину. Показаны все внешние силы, действующие на автомобиль. (b) Силы, действующие на автомобиль, переносятся на координатную плоскость (диаграмма свободного тела) для упрощения анализа.(c) Эвакуатор может создавать большую внешнюю силу при той же массе и, следовательно, большее ускорение.

Из этого примера вы можете видеть, что разные силы, действующие на одну и ту же массу, вызывают разное ускорение. На (Рис.) (А) двое учеников толкают машину с водителем. Показаны стрелки, представляющие все внешние силы. Интересующая система — это автомобиль и его водитель. Вес [латекс] \ overset {\ to} {w} [/ latex] системы и основание [латекс] \ overset {\ to} {N} [/ latex] также показаны для полноты и предполагается отменить (потому что не было вертикального движения и дисбаланса сил в вертикальном направлении, чтобы создать изменение в движении).Вектор [latex] \ overset {\ to} {f} [/ latex] представляет трение, действующее на автомобиль, и действует влево, противодействуя движению автомобиля. (Мы обсудим трение более подробно в следующей главе.) На (Рисунок) (b) все внешние силы, действующие на систему, складываются вместе, образуя результирующую силу [латекс] {\ overset {\ to} {F}} _ {\ text {net}}. [/ latex] Диаграмма свободного тела показывает все силы, действующие на интересующую систему. Точка представляет собой центр масс системы. Каждый вектор силы простирается от этой точки.{\ prime}}> \ overset {\ to} {a}) [/ latex], когда эвакуатор тянет машину.

Кажется разумным, что ускорение будет прямо пропорционально чистой внешней силе, действующей на систему, и в том же направлении. Это предположение было проверено экспериментально и проиллюстрировано на (Рисунок). Чтобы получить уравнение для второго закона Ньютона, сначала запишем соотношение ускорения [латекс] \ overset {\ to} {a} [/ latex] и чистой внешней силы [латекс] {\ overset {\ to} {F}} _ {\ text {net}} [/ latex] как пропорциональность

[латекс] \ overset {\ to} {a} \ propto {\ overset {\ to} {F}} _ {\ text {net}} [/ latex]

, где символ [латекс] \ propto [/ latex] означает «пропорционально.”(Напомним из книги« Силы », что чистая внешняя сила является векторной суммой всех внешних сил и иногда обозначается как [латекс] \ sum \ overset {\ to} {F}. [/ Latex]) Эта пропорциональность показывает то, что мы сказали на словах — ускорение прямо пропорционально чистой внешней силе. После выбора интересующей системы определите внешние силы и игнорируйте внутренние. Было бы огромным упрощением игнорировать многочисленные внутренние силы, действующие между объектами внутри системы, такие как мышечные силы в телах учеников, не говоря уже о бесчисленных силах между атомами в объектах.Тем не менее, это упрощение помогает нам решать некоторые сложные проблемы.

Также кажется разумным, что ускорение должно быть обратно пропорционально массе системы. Другими словами, чем больше масса (инерция), тем меньше ускорение, создаваемое данной силой. Как показано на (Рисунок), та же самая чистая внешняя сила, приложенная к баскетбольному мячу, вызывает гораздо меньшее ускорение, когда она применяется к кроссоверу. Пропорциональность записывается как

[латекс] a \ propto \ frac {1} {m}, [/ latex]

, где м, — масса системы, а — — величина ускорения.Эксперименты показали, что ускорение прямо обратно пропорционально массе, так же как оно прямо пропорционально чистой внешней силе.

Рисунок 5.11 Одна и та же сила, действующая на системы разной массы, вызывает разное ускорение. (a) Баскетболист толкает баскетбольный мяч, чтобы сделать передачу. (Игнорируйте влияние силы тяжести на мяч.) (B) Тот же игрок оказывает идентичную силу на остановившийся внедорожник и производит гораздо меньшее ускорение. (c) Диаграммы свободного тела идентичны, что позволяет напрямую сравнить две ситуации.По мере того, как вы решите больше задач и научитесь рисовать их в Рисование диаграмм свободного тела, появится серия шаблонов для диаграмм свободного тела.

Было обнаружено, что ускорение объекта зависит только от чистой внешней силы и массы объекта. Комбинирование двух только что приведенных соотношений дает второй закон Ньютона .

Второй закон движения Ньютона

Ускорение системы прямо пропорционально чистой внешней силе, действующей на систему, и в том же направлении, и обратно пропорционально ее массе.В форме уравнения второй закон Ньютона равен

[латекс] \ overset {\ to} {a} = \ frac {{\ overset {\ to} {F}} _ {\ text {net}}} {m}, [/ latex]

где [latex] \ overset {\ to} {a} [/ latex] — это ускорение, [latex] {\ overset {\ to} {F}} _ {\ text {net}} [/ latex] — это чистая сила, а м — масса. Это часто записывается в более привычной форме

[латекс] {\ overset {\ to} {F}} _ {\ text {net}} = \ sum \ overset {\ to} {F} = m \ overset {\ to} {a}, [/ латекс ]

, но первое уравнение дает больше понимания того, что означает второй закон Ньютона.Если рассматривать только величину силы и ускорения, это уравнение можно записать в более простой скалярной форме:

[латекс] {F} _ {\ text {net}} = ma. [/ латекс]

Закон — это причинно-следственная связь между тремя величинами, которая не просто основана на их определениях. Справедливость второго закона основана на экспериментальной проверке. Диаграмма свободного тела, которую вы научитесь рисовать в «Рисование диаграмм свободного тела», является основой для написания второго закона Ньютона.

Пример

Какое ускорение может дать человек, толкая газонокосилку?

Предположим, что чистая внешняя сила (толчок минус трение), действующая на газонокосилку, составляет 51 Н (около 11 фунтов) параллельно земле ((Рисунок)). Масса косилки 24 кг. Какое у него ускорение?

Рисунок 5.12 (a) Полезное усилие на газонокосилке составляет 51 Н. вправо. С какой скоростью газонокосилка ускоряется вправо? (б) Показана диаграмма свободного тела для этой задачи.

Стратегия

Эта проблема связана только с движением в горизонтальном направлении; нам также дана чистая сила, обозначенная одним вектором, но мы можем подавить векторную природу и сосредоточиться на применении второго закона Ньютона. Поскольку даны [latex] {F} _ {\ text {net}} [/ latex] и m , ускорение можно рассчитать непосредственно из второго закона Ньютона как [latex] {F} _ {\ text {net} } = ma. [/ латекс]

Решение

Величина ускорения a равна [latex] a = {F} _ {\ text {net}} \ text {/} m [/ latex].{2}. [/ латекс]

Значение

Направление ускорения совпадает с направлением результирующей силы, параллельной земле. Это результат векторной связи, выраженной во втором законе Ньютона, то есть вектор, представляющий чистую силу, является скалярным кратным вектору ускорения. В этом примере нет информации об отдельных внешних силах, действующих на систему, но мы можем кое-что сказать об их относительных величинах.Например, сила, прикладываемая человеком, толкающим косилку, должна быть больше, чем трение, препятствующее движению (поскольку мы знаем, что косилка движется вперед), а вертикальные силы должны нейтрализоваться, потому что в вертикальном направлении не происходит ускорение (косилка движется только по горизонтали). Обнаруженное ускорение достаточно мало, чтобы быть приемлемым для человека, толкающего косилку. Такое усилие не продлится слишком долго, потому что человек скоро наберет максимальную скорость.

Проверьте свое понимание

На момент запуска HMS Titanic был самым массивным из когда-либо построенных мобильных объектов с массой [латекс] 6.{2} [/ латекс]

В предыдущем примере мы имели дело с чистой силой только для простоты. Однако на газонокосилку действует несколько сил. Вес [латекс] \ overset {\ to} {w} [/ latex] (подробно описанный в разделе «Масса и вес») тянет газонокосилку вниз к центру Земли; это создает контактное усилие на земле. Земля должна оказывать на газонокосилку направленную вверх силу, известную как нормальная сила [латекс] \ overset {\ to} {N} [/ latex], которую мы определяем в «Общих силах». Эти силы уравновешены и поэтому не вызывают вертикального ускорения.В следующем примере мы показываем обе эти силы. Продолжая решать проблемы, используя второй закон Ньютона, не забудьте показать множественные силы.

Пример

Какая сила больше?

(a) Автомобиль, показанный на (Рисунок), движется с постоянной скоростью. Какая сила больше, [латекс] {\ overset {\ to} {F}} _ {\ text {engine}} [/ latex] или [latex] {\ overset {\ to} {F}} _ {\ text {трение}} [/ латекс]? Объяснять.

(b) Эта же машина сейчас ускоряется вправо. Какая сила больше, [латекс] {\ overset {\ to} {F}} _ {\ text {engine}} [/ latex] или [latex] {\ overset {\ to} {F}} _ {\ text {трение}}? [/ latex] Объясните.

Рисунок 5.13 Автомобиль показан (а) движущимся с постоянной скоростью и (б) ускоряющимся. Как соотносятся силы, действующие на автомобиль в каждом конкретном случае? а) Что знание того, что автомобиль движется с постоянной скоростью, говорит нам о чистой горизонтальной силе, действующей на автомобиль, по сравнению с силой трения? б) Что знание того, что автомобиль ускоряется, говорит нам о горизонтальной силе, действующей на автомобиль, по сравнению с силой трения?

Стратегия

Мы должны рассмотреть первый и второй законы Ньютона, чтобы проанализировать ситуацию.Нам нужно решить, какой закон применяется; это, в свою очередь, расскажет нам о соотношении сил.

Решение

Силы равны. Согласно первому закону Ньютона, если результирующая сила равна нулю, скорость постоянна.
В этом случае [латекс] {\ overset {\ to} {F}} _ {\ text {engine}} [/ latex] должен быть больше, чем [латекс] {\ overset {\ to} {F}} _ {\ text {friction}}. [/ latex] Согласно второму закону Ньютона, для ускорения требуется чистая сила.

Значение

Эти вопросы могут показаться тривиальными, но обычно на них отвечают неверно. Чтобы автомобиль или любой другой объект двинулся с места, его нужно разогнать до желаемой скорости; для этого требуется, чтобы сила двигателя была больше силы трения. Когда автомобиль движется с постоянной скоростью, результирующая сила должна быть равна нулю; в противном случае автомобиль будет ускоряться (набирать скорость). Чтобы решить проблемы, связанные с законами Ньютона, мы должны понимать, применять ли первый закон Ньютона (где [latex] \ sum \ overset {\ to} {F} = \ overset {\ to} {0} [/ latex]) или второй закон Ньютона. закон (где [латекс] \ sum \ overset {\ to} {F} [/ latex] не равен нулю).Это станет очевидным, когда вы увидите больше примеров и попытаетесь решить проблемы самостоятельно.

Пример

Какая ракетная тяга ускоряет этот снегоход?

До пилотируемых космических полетов ракетные сани использовались для испытания самолетов, ракетного оборудования и физиологических воздействий на людей на высоких скоростях. Они состояли из платформы, которая была установлена на одной или двух направляющих и приводилась в движение несколькими ракетами.

Рассчитайте величину силы, прилагаемой каждой ракетой, которая называется ее тягой T , для четырехракетной двигательной установки, показанной на (Рисунок).{2} [/ latex], масса системы 2100 кг, сила трения, препятствующая движению, 650 Н.

Рис. 5.14 Салазки испытывают ракетную тягу, которая ускоряет их вправо. Каждая ракета создает одинаковую тягу T. Система здесь представляет собой салазки, их ракеты и их всадник, поэтому никакие силы между этими объектами не учитываются. Стрелка, обозначающая трение [латекс] (\ overset {\ to} {f}) [/ latex], нарисована больше, чем масштаб.

Стратегия

Хотя силы действуют как вертикально, так и горизонтально, мы предполагаем, что вертикальные силы компенсируются, потому что нет вертикального ускорения.Это оставляет нам только горизонтальные силы и более простую одномерную задачу. Направления указываются знаками плюс или минус, при этом вправо принимается за положительное направление. См. Диаграмму свободного тела на (Рисунок).

Решение

Поскольку ускорение, масса и сила трения даны, мы начнем со второго закона Ньютона и ищем способы найти тягу двигателей. Мы определили направление силы и ускорения как действующее «вправо», поэтому в расчетах нам нужно учитывать только величины этих величин.Следовательно, мы начинаем с

[латекс] {F} _ {\ text {net}} = ma [/ latex]

где [латекс] {F} _ {\ text {net}} [/ latex] — чистая сила в горизонтальном направлении. Из рисунка видно, что тяга двигателя увеличивается, а трение противодействует. В форме уравнения чистая внешняя сила равна

[латекс] {F} _ {\ text {net}} = 4T-f. [/ латекс]

Подставляя это во второй закон Ньютона, получаем

[латекс] {F} _ {\ text {net}} = ma = 4T-f. [/ латекс]

Используя небольшую алгебру, мы решаем общую тягу 4 T :

[латекс] 4T = ma + f.{2} [/ latex].) Хотя живые предметы больше не используются, с помощью ракетных саней была получена сухопутная скорость 10 000 км / ч.

В этом примере, как и в предыдущем, интересующая система очевидна. В последующих примерах мы увидим, что выбор интересующей системы имеет решающее значение, и этот выбор не всегда очевиден.

Второй закон Ньютона — это больше, чем определение; это соотношение между ускорением, силой и массой. Это может помочь нам делать прогнозы. Каждую из этих физических величин можно определить независимо, поэтому второй закон говорит нам что-то основное и универсальное о природе.{2} [/ латекс]

Составная форма второго закона Ньютона

Мы разработали второй закон Ньютона и представили его в виде векторного уравнения (рисунок). Это векторное уравнение можно записать в виде трехкомпонентных уравнений:

[латекс] \ sum {\ overset {\ to} {F}} _ {x} = m {\ overset {\ to} {a}} _ {x}, \, \ sum {\ overset {\ to} {F}} _ {y} = m {\ overset {\ to} {a}} _ {y}, \, \ text {and} \, \ sum {\ overset {\ to} {F}} _ { z} = m {\ overset {\ to} {a}} _ {z}. [/ латекс]

Второй закон — это описание того, как тело механически реагирует на окружающую среду.Влияние окружающей среды — это чистая сила [латекс] {\ overset {\ to} {F}} _ {\ text {net}}, [/ latex], реакция тела — ускорение [латекс] \ overset {\ to } {a}, [/ latex] и сила отклика обратно пропорциональна массе м . Чем больше масса объекта, тем меньше его реакция (его ускорение) на влияние окружающей среды (заданная результирующая сила). Следовательно, масса тела является мерой его инерции, как мы объясняли в Первом законе Ньютона.

Пример

Сила на футбольном мяче

А 0.{2}. [/ latex] Найдите (а) результирующую силу, действующую на мяч, и (б) величину и направление результирующей силы.

Стратегия

Векторы в формате [latex] \ hat {i} [/ latex] и [latex] \ hat {j} [/ latex], которые указывают направление силы по оси x и оси y , соответственно, поэтому мы применяем второй закон Ньютона в векторной форме.

Решение

Применяем второй закон Ньютона:
[латекс] {\ overset {\ to} {F}} _ {\ text {net}} = m \ overset {\ to} {a} = (0.{-1} (\ frac {2.80} {1.20}) = 66,8 \ text {°}. [/ латекс]

Значение

Мы должны помнить, что второй закон Ньютона является векторным уравнением. В (а) мы умножаем вектор на скаляр, чтобы определить результирующую силу в векторной форме. Хотя векторная форма дает компактное представление вектора силы, она не говорит нам, насколько он «большой» или куда он идет, в интуитивно понятных терминах. В (b) мы определяем действительный размер (величину) этой силы и направление, в котором она движется.{2} [/ латекс].

Стратегия

Векторное деление не определено, поэтому [latex] m = {\ overset {\ to} {F}} _ {\ text {net}} \ text {/} \ overset {\ to} {a} [/ latex] не может быть выполнено. Однако масса m является скаляром, поэтому мы можем использовать скалярную форму второго закона Ньютона, [latex] m = {F} _ {\ text {net}} \ text {/} a [/ latex].

Решение

Мы используем [latex] m = {F} _ {\ text {net}} \ text {/} a [/ latex] и подставляем величины двух векторов: [latex] {F} _ {\ text {net }} = 600.{2}} = 3000 \, \ text {кг}. [/ латекс]

Значение

Сила и ускорение были даны в формате [latex] \ hat {i} [/ latex] и [latex] \ hat {j} [/ latex], но ответ, масса m , является скаляром и, следовательно, не указывается в формах [латекс] \ шляпа {i} [/ латекс] и [латекс] \ шляпа {j} [/ латекс].

Пример

Несколько сил на частицу

На частицу массы [латекс] m = 4.0 \, \ text {kg} [/ latex] действуют четыре силы величин. [латекс] {F} _ {1} = 10.0 \, \ text {N}, \, {F} _ {2} = 40.0 \, \ text {N}, \, {F} _ {3} = 5.0 \, \ text {N}, \, \ text {and} \, {F} _ {4} = 2.0 \, \ text {N} [/ latex], с направлениями, показанными на диаграмме свободного тела на (Рисунок). Что такое ускорение частицы?

Рис. 5.15 Четыре силы в плоскости xy действуют на частицу массой 4,0 кг.

Стратегия

Поскольку это двумерная задача, мы должны использовать диаграмму свободного тела. Во-первых, [latex] {\ overset {\ to} {F}} _ {1} [/ latex] необходимо разделить на компоненты x и y .Затем мы можем применить второй закон в каждом направлении.

Решение

Рисуем диаграмму свободного тела, как показано на (Рисунок). Теперь применим второй закон Ньютона. Мы рассматриваем все векторы, разделенные на компоненты x и y :

[латекс] \ begin {array} {cccc} \ sum {F} _ {x} = m {a} _ {x} \ hfill & & & \ sum {F} _ {y} = m {a} _ {y} \ hfill \\ {F} _ {1x} — {F} _ {3x} = m {a} _ {x} \ hfill & & & {F} _ {1y} + {F} _ {4y } — {F} _ {2y} = m {a} _ {y} \ hfill \\ {F} _ {1} \, \ text {cos} \, 30 \ text {°} — {F} _ { 3x} = m {a} _ {x} \ hfill & & & {F} _ {1} \ text {sin} \, 30 \ text {°} + {F} _ {4y} — {F} _ { 2y} = m {a} _ {y} \ hfill \\ (10.{2} [/ latex] направлен на [латекс] 276 \ text {°} [/ latex] к положительной оси x .

Значение

В повседневной жизни можно найти множество примеров, когда три или более сил действуют на один объект, например, кабели, идущие от моста Золотые Ворота, или футболиста, которого атакуют три защитника. Мы видим, что решение этого примера является просто продолжением того, что мы уже сделали.

Проверьте свое понимание

На автомобиль действуют силы, как показано ниже.Масса автомобиля 1000,0 кг. Дорога скользкая, поэтому трение можно не учитывать. а) Какова чистая сила, действующая на машину? б) Какое ускорение у машины?

Покажи ответ

а. [латекс] 159.0 \ hat {i} +770.0 \ hat {j} \, \ text {N} [/ latex]; б. [латекс] 0,1590 \ hat {i} +0,7700 \ hat {j} \, \ text {N} [/ latex]

Второй закон и импульс Ньютона

Ньютон фактически сформулировал свой второй закон в терминах количества движения: «Мгновенная скорость изменения количества движения тела равна чистой силе, действующей на тело.»(« Мгновенная скорость »подразумевает, что задействована производная.) Это может быть задано векторным уравнением

[латекс] {\ overset {\ to} {F}} _ {\ text {net}} = \ frac {d \ overset {\ to} {p}} {dt}. [/ латекс]

Это означает, что второй закон Ньютона обращается к центральному вопросу движения: что вызывает изменение движения объекта? Импульс был описан Ньютоном как «количество движения», способ объединения скорости объекта и его массы. Мы посвящаем линейный импульс и столкновения изучению импульса , импульса .

На данный момент достаточно определить импульс [латекс] \ overset {\ to} {p} [/ latex] как произведение массы объекта m и его скорости [латекс] \ overset {\ to} {v} [/ latex]:

[латекс] \ overset {\ to} {p} = m \ overset {\ to} {v}. [/ латекс]

Поскольку скорость — вектор, импульс тоже.

Импульс легко визуализировать. Поезд, движущийся со скоростью 10 м / с, имеет больше импульса, чем поезд, движущийся со скоростью 2 м / с. В повседневной жизни мы говорим об одной спортивной команде как о «имеющей импульс», когда она набирает очки против команды соперника.

Если подставить (рисунок) в (рисунок), то получим

[латекс] {\ overset {\ to} {F}} _ {\ text {net}} = \ frac {d \ overset {\ to} {p}} {dt} = \ frac {d (m \ overset {\ to} {v})} {dt}. [/ латекс]

Когда м постоянный, мы имеем

[латекс] {\ overset {\ to} {F}} _ {\ text {net}} = m \ frac {d (\ overset {\ to} {v})} {dt} = m \ overset {\ to} {a}. [/ латекс]

Таким образом, мы видим, что импульсная форма второго закона Ньютона сводится к форме, приведенной ранее в этом разделе.

Физика гонок, часть 1: Перенос веса

От: Dr.Брайан Бекман «Физика гонок»

Поймите обоснование

Большинство автокроссеров и гонщиков рано осознают важность балансировки автомобиля. Научиться делать это последовательно и автоматически — одна из важнейших составляющих того, чтобы стать по-настоящему хорошим водителем. В то время как навыки балансировки автомобиля обычно преподаются в школах водителей, их обоснование обычно не объясняется должным образом. Это обоснование исходит из простой физики. Понимание физики вождения не только помогает стать лучше водителем, но и увеличивает удовольствие от вождения.Если вы знаете глубинные причины, по которым вам следует делать определенные вещи, вы лучше запомните их и быстрее продвинетесь к полной усвоению навыков.

Балансировка

Балансировка автомобиля — это управление переносом веса с помощью газа, тормозов и рулевого управления. В этой статье объясняется физика переноса веса. Вы часто слышите, как тренеры и водители говорят, что при торможении вес переносится на переднюю часть автомобиля и может вызвать чрезмерную поворачиваемость. Точно так же при ускорении вес смещается назад, вызывая недостаточную управляемость, а при прохождении поворотов вес смещается в противоположную сторону, разгружая внутренние шины.Но почему при этих маневрах смещается вес? Как можно сместить вес, если в машине все прикручено и привязано? Вкратце, причина в том, что инерция действует через центр тяжести (CG) автомобиля, который находится над землей, а силы сцепления действуют на уровне земли через пятна контакта шин. Эффект переноса веса пропорционален высоте ЦТ над землей. Более плоский автомобиль с более низким CG управляется лучше и быстрее, потому что перенос веса не такой резкий, как в высоком автомобиле.

Остальная часть этой статьи объясняет, как силы инерции и адгезии вызывают перенос веса по законам Ньютона. Статья начинается с элементов и сводится к некоторым простым уравнениям, которые можно использовать для расчета переноса веса в любом автомобиле, зная только колесную базу, высоту ЦТ, статическое распределение веса и колею или расстояние между шинами в поперечном направлении. машина. Эти цифры приводятся в инструкциях по эксплуатации и в большинстве журналистских обзоров автомобилей.

Законы Ньютона

Большинство людей помнят законы Ньютона из школьной физики.Это фундаментальные законы, которые применимы ко всем большим объектам во Вселенной, например, к автомобилям. В контексте нашего гоночного приложения это:

Первый закон: автомобиль, движущийся по прямой с постоянной скоростью, будет продолжать движение до тех пор, пока на него не будет действовать внешняя сила. Единственная причина, по которой автомобиль на нейтрали не будет двигаться по инерции вечно, заключается в том, что трение, внешняя сила, постепенно замедляет автомобиль. Трение возникает от шин о землю и обтекающего машину воздуха. Тенденция автомобиля продолжать движение так же, как он движется, — это инерция автомобиля, и эта тенденция сосредоточена в точке ЦТ.

Второй закон: Когда к автомобилю прилагается сила, изменение движения пропорционально силе, деленной на массу автомобиля. Этот закон выражается знаменитым уравнением F = ma, где F — сила, m — масса автомобиля, а a — ускорение или изменение движения автомобиля. Большая сила вызывает более быстрые изменения в движении, а более тяжелый автомобиль медленнее реагирует на силы. Второй закон Ньютона объясняет, почему быстрые автомобили мощные и легкие. Чем больше F и меньше m у вас есть, тем больше a вы можете получить. Третий закон: Каждой силе, действующей на автомобиль со стороны другого объекта, например земли, соответствует равная и противоположная сила, действующая на объект со стороны автомобиля. Когда вы нажимаете на тормоза, вы заставляете колеса толкаться вперед по земле, а земля толкается назад. Пока шины остаются на машине, земля, давящая на них, замедляет машину.

Анализ торможения

Перенос веса при ускорении и прохождении поворотов — всего лишь вариации на тему. Пока не будем рассматривать такие тонкости, как подвеска и прогиб шин.Эти эффекты очень важны, но второстепенны. На рисунке показан автомобиль и силы, действующие на него во время маневра торможения «один g». Один g означает, что общая тормозная сила равна весу автомобиля, скажем, в фунтах.

На этом рисунке черно-белая «круговая тарелка» в центре — это ЦТ. G — это сила тяжести, которая тянет автомобиль к центру Земли. Это вес машины; вес — это просто другое слово для обозначения силы тяжести. Это факт природы, полностью объясненный только Альбертом Эйнштейном, что гравитационные силы действуют через ЦТ объекта, как и инерция.Этот факт можно объяснить на более глубоком уровне, но такое объяснение уведет нас слишком далеко от темы переноса веса.

Lf — это подъемная сила, оказываемая землей на переднюю шину, а Lr — подъемная сила на заднюю шину. Эти подъемные силы столь же реальны, как и те, которые удерживают самолет в воздухе, и они не дают автомобилю провалиться сквозь землю к центру Земли.

Мы не часто замечаем силы, которые земля оказывает на объекты, потому что они такие обычные, но они лежат в основе динамики автомобиля.Причина в том, что величина этих сил определяет способность шины заедать, а дисбаланс между передней и задней подъемными силами приводит к недостаточной и избыточной поворачиваемости. На рисунке показаны только силы, действующие на автомобиль, а не силы, действующие на землю и ЦТ Земли. Третий закон Ньютона требует, чтобы эти равные и противоположные силы существовали, но нас беспокоит только то, как земля и гравитация Земли влияют на машину.

Если бы автомобиль стоял на месте или двигался по инерции, а его распределение веса было бы 50-50, то Lf было бы таким же, как Lr.Всегда бывает, что Lf плюс Lr равняется G, весу автомобиля. Почему? Из-за первого закона Ньютона. Автомобиль не меняет своего движения в вертикальном направлении, по крайней мере, до тех пор, пока он не поднимается в воздух, поэтому общая сумма всех сил в вертикальном направлении должна быть равна нулю. G указывает вниз и противодействует сумме Lf и Lr, которые указывают вверх.

Торможение приводит к тому, что Lf становится больше Lr. Буквально «загорается задняя часть», как часто приходится слышать от гонщиков. Рассмотрим на диаграмме передние и задние тормозные силы Bf и Br.Они толкают назад шины, которые толкают колеса, которые толкают детали подвески, которые толкают остальную часть автомобиля, замедляя его. Но эти силы действуют на уровне земли, а не на уровне ЦТ. Тормозные силы косвенно замедляют автомобиль, толкая его на уровне земли, в то время как инерция автомобиля «пытается заставить его двигаться вперед как единое целое на уровне CG».

Тормозные силы создают тенденцию к вращению или крутящий момент относительно ЦТ. Представьте, что вы вытаскиваете скатерть из-под очков и канделябров.Эти предметы будут иметь тенденцию опрокидываться или поворачиваться, и эта тенденция тем больше для более высоких предметов, и тем сильнее, чем сильнее вы тянете за ткань. Тенденция вращения автомобиля при торможении обусловлена идентичной физикой.
Тормозной момент действует таким образом, что автомобиль ставится на нос. Поскольку машина на самом деле не едет на носу (мы надеемся), по первому закону Ньютона этой тенденции должны противодействовать другие силы. G не может этого делать, поскольку проходит прямо через центр тяжести.Единственными силами, которые могут противодействовать этой тенденции, являются подъемные силы, и единственный способ, которым они могут это сделать, — это сделать Lf больше, чем Lr. Буквально во время торможения земля сильнее давит на передние колеса, чтобы машина не опрокидывалась вперед.

Если у вас есть цифры ускорения в единицах ge, скажем, от G-аналитика или другого устройства, просто умножьте их на вес автомобиля, чтобы получить силы ускорения (второй закон Ньютона!). Перенос веса во время поворота можно проанализировать аналогичным образом, когда колея автомобиля заменяет колесную базу, а d всегда составляет 50% (если вы не учитываете вес водителя).Те из вас, у кого есть научное или инженерное образование, могут получить удовольствие от самостоятельного вывода этих уравнений. Уравнения для автомобиля, выполняющего комбинацию торможения и прохождения поворота, как в маневре торможения по бездорожью, намного сложнее и требуют некоторых математических уловок для получения.

Теперь вы знаете, почему происходит перенос веса. Следующая тема, которая приходит на ум, — это физика сцепления шин, которая объясняет, как перенос веса может привести к недостаточной и избыточной поворачиваемости.

Артикул:
Dr.Брайан Бекман — Физика гонок

Автомобиль-разгонщик

Автомобиль с передним приводом ускоряется из состояния покоя так, что все колеса катятся без пробуксовки. В каком направлении действует сила трения на передние колеса? Это статическое трение или кинетическое трение?

Мы также должны ответить на этот вопрос — в каком направлении действует сила трения на задних колесах, статическая или кинетическая? Сила на задние колеса составляет:

кинетическое трение, действующее в направлении вашего движения.
кинетическое трение, действующее противоположно направлению вашего движения.
статическое трение, действующее в направлении вашего движения.
Статическое трение, действующее противоположно направлению вашего движения.

Помните, что этот анализ предполагает, что автомобиль ускоряется вперед. Самый простой способ выяснить, что происходит с трением, — это посмотреть, что происходит, когда вы выключаете трение.

При полном отсутствии трения и остановке автомобиля нажатие на педаль акселератора заставляет передние колеса вращаться по часовой стрелке.Они крутятся по поверхности без трения, задние колеса ничего не делают, и машина никуда не едет.

Трение передних колес препятствует вращению, поэтому оно должно указывать в том направлении, в котором автомобиль хочет ехать. Чтобы передние колеса катились без пробуксовки, трение должно быть статическим.

Если включить трение только по передним колесам, машина разгоняется вперед, а задние колеса волочатся по дороге без пробуксовки.

Силы действующие на автомобиль при движении

Тяговая сила

Сила сцепления колес с дорогой

Сила сопротивления воздуха

Сила сопротивления качению

(adsbygoogle=window.adsbygoogle||[]).push({}); Сила сопротивления разгону

Центр тяжести

Силы, действующие на автомобиль

Силы, действующие на автомобиль

Силы, действующие на автомобиль во время его движения

Смотрите также:

7. Силы, действующие на автомобиль при прямолинейном движении.

8. Внешняя скоростная характеристика двс. Хар. Точки, методы построения.

9. Силы сопротивления движению автомобиля(качения, подъему, дороги)

10. Сила сопротивления воздуха. Коэф. Лобового сопротивления. Коэф. Обтекаемости.

Силы, действующие на электромобиль (автомобиль)

Специальные термины и обозначения для ходовой части автомобиля Volkswagen

Расчётное положение

Установочная высота

Программа помощи на дорогах «Гарантия Мобильности» от Volkswagen в России

ДИНАМИКА АВТОМОБИЛЯ

ЦЕНТРОБЕЖНАЯ СИЛА

ИНЕРЦИЯ

GCSE Forces | Пересмотрите трение и сопротивление при торможении

Глава 4 Концепции

Глава 4

5.3 Второй закон Ньютона | University Physics Volume 1

Сила и ускорение

Второй закон движения Ньютона

Пример

Какое ускорение может дать человек, толкая газонокосилку?

Стратегия

Решение

Значение

Проверьте свое понимание

Пример

Какая сила больше?

Стратегия

Решение

Значение

Пример

Какая ракетная тяга ускоряет этот снегоход?

Стратегия

Решение

Составная форма второго закона Ньютона

Пример

Сила на футбольном мяче

Стратегия

Решение

Значение

Стратегия

Решение

Значение

Пример

Несколько сил на частицу

Стратегия

Решение

Значение

Проверьте свое понимание

Второй закон и импульс Ньютона

Физика гонок, часть 1: Перенос веса

Поймите обоснование

Балансировка

Законы Ньютона

Анализ торможения

Автомобиль-разгонщик

Автор: alexxlab

Добавить комментарий Отменить ответ

Рубрики

Сила сопротивления разгону