Геометрические размеры кузова Daewoo.
Информация о геометрических размерах и параметрах кузова, с фотографиями контрольных точек кузовов продукции компании DAEWOO.
Геометрические размеры кузова 2000г. Daewoo Lanos.
СКАЧАТЬГеометрические размеры кузова 2000г. Daewoo Leganza.
СКАЧАТЬГеометрические размеры кузова 2000г. Daewoo Nubira.
СКАЧАТЬГеометрические размеры кузова Daewoo.
Контрольные точки геометрии кузова.
Геометрические размеры DAEWOO ARCADIA SEDAN модель WA19 (1994—г.)
СКАЧАТЬГеометрические размеры DAEWOO ESPERO NOTCHBACK TYPE JF19 (1990-1995г.)
СКАЧАТЬГеометрические размеры DAEWOO ESPERO 4-DOOR SEDAN (1995-2001г.)
СКАЧАТЬГеометрические размеры DAEWOO NEXIA, CIELO, RACER 3-дверный HATCHBACK (1995—г.)
СКАЧАТЬГеометрические размеры DAEWOO NEXIA, CIELO, RACER 4-дверный SEDAN (1995—г.)
СКАЧАТЬГеометрические размеры DAEWOO NEXIA, CIELO, RACER 5-дверный HATCHBACK (1995—г.
Геометрические размеры DAEWOO ESPERO 4 -дверный SEDAN (1995—г.)
СКАЧАТЬГеометрические размеры DAEWOO ESPERO NOTCHBACK модель JF19 (1990—г.)
СКАЧАТЬГеометрические размеры DAEWOO EVANDA 4-дверный SEDAN (2003-2004г.)
СКАЧАТЬГеометрические размеры DAEWOO LANOS 3-дверный HATCHBACK (1997—г.)
СКАЧАТЬГеометрические размеры DAEWOO LANOS 4-дверный SEDAN (1997—г.)
СКАЧАТЬГеометрические размеры DAEWOO LANOS 5-дверный HATCHBACK (1997—г.)
СКАЧАТЬГеометрические размеры DAEWOO LACETTI 5-дверный HATCHBACK (2004—г.)
СКАЧАТЬГеометрические размеры DAEWOO LEMANS 4-дверный SEDAN модель TF19 (1986—г. )
СКАЧАТЬГеометрические размеры DAEWOO LEGANZA 4-дверный SEDAN (1997—г.)
СКАЧАТЬГеометрические размеры DAEWOO LUBLIN II TRUCK (1998—г.)
СКАЧАТЬГеометрические размеры DAEWOO LUBLIN II VAN (1998—г.)
СКАЧАТЬГеометрические размеры DAEWOO KALOS 4-дверный SEDAN (2003-2004г.)
СКАЧАТЬГеометрические размеры DAEWOO KALOS 5-дверный HATCHBACK (2003-2004г. )
)
Геометрические размеры DAEWOO KORANDO 4WD WAGON (1997-2002г.)
СКАЧАТЬГеометрические размеры DAEWOO MATIZ 5-дверный (1998—г.)
СКАЧАТЬГеометрические размеры DAEWOO NUBIRA 4-дверный SEDAN (1997—г.)
СКАЧАТЬГеометрические размеры DAEWOO NUBIRA 5-дверный HATCHBACK (1997—г.)
СКАЧАТЬГеометрические размеры DAEWOO NUBIRA 5-дверный WAGON (1997—г. )
СКАЧАТЬГеометрические размеры DAEWOO NUBIRA 4-дверный SEDAN. (1999-2003г.)
СКАЧАТЬГеометрические размеры DAEWOO NUBIRA 5-дверный WAGON. (2000-2004г.)
СКАЧАТЬГеометрические размеры DAEWOO NUBIRA 5-дверный WAGON.. (2004—г.)
СКАЧАТЬГеометрические размеры DAEWOO NUBIRA LACETTI 4-дверный SEDAN (2003-2004г.)
СКАЧАТЬГеометрические размеры DAEWOO TICO 5-дверный HATCHBACK (1992—г.)
Геометрические размеры DAEWOO TACUMA, REZZO 5-дверный WAGON, MPV (2000-2004г.)
СКАЧАТЬИздательство: Третий Рим
Автор: Погребной С.Н.
Страниц: 384 Год: 2009
Размер: 40Мб.
Для работников СТО и автосервисов. Поддерживать машину в надлежащем рабочем состоянии, экономить время и деньги. Мануал содержит более 2000 цветных снимков, досконально отображающих процесс пошагового ремонта Дэу Нексия, в том числе ремонта двигателя, технические характеристики автомобиля, перечни возможных неисправностей и рекомендации по их устранению.
СКАЧАТЬ
Запросы: Геометрические размеры кузова DAEWOO, геометрия кузова DAEWOO, кузовные размеры DAEWOO, контрольные кузовные размеры DAEWOO, геометрия контрольных точек DAEWOO, размеры кузова и контрольные точки DAEWOO, размеры DAEWOO, body dimensions DAEWOO.
Проверка геометрии кузова автомобиля. Подробно об измерении
В общем процессе ремонта кузова автомобиля очень важную роль играет процесс измерения геометрических параметров структурных элементов. Машину нельзя правильно отремонтировать без возврата контрольных точек кузова в первоначальное положение, определённое производителем. Для этого нужно делать измерения точно и по нескольку раз в процессе ремонта.
Для этого нужно делать измерения точно и по нескольку раз в процессе ремонта.
Существует несколько разновидностей измерительного оборудования. В целом, их можно разделить на 5 базовых типов:
- Линейки, рулетка, специальный циркуль
- Универсальные измерительные системы (механические)
- Специализированные системы с креплением
- Универсальные лазерные системы
- Компьютерные/электронные системы
Подробнее об измерительных системах можно прочитать здесь.
Измерения геометрии кузова автомобиля условно можно разделить на три вида:
- Измерение между контрольными точками. Осуществляется, чтобы сделать быструю проверку перед ремонтом и в процессе ремонта. Измерения производятся простой рулеткой, а также линейкой для проверки геометрии кузова.
- Сравнительное (сравниваются расстояния симметричных точек на разных сторонах кузова).
 Сравнительное измерение является универсальным самым быстрым и лёгким методом проверки геометрии повреждённого кузова. Производятся сравнения диагональных расстояний между симметричными точками. Можно измерять, сравнивая повреждённую часть автомобиля с неповреждённой.
Сравнительное измерение является универсальным самым быстрым и лёгким методом проверки геометрии повреждённого кузова. Производятся сравнения диагональных расстояний между симметричными точками. Можно измерять, сравнивая повреждённую часть автомобиля с неповреждённой. - 3‑х мерное измерение (определяется пространственное положение контрольных точек относительно базовых плоскостей при помощи специального оборудования).
Измерения позволяют определить степень главных повреждений, выявить второстепенные повреждения и определить план восстановления.
Контрольные точки геометрии кузова автомобиля
Большинство контрольных точек представляют собой отверстия в структурных элементах кузова. Вообще, в качестве контрольных точек могут выступать любые стационарные точки на структурных элементах кузова. Можно мерить , к примеру, между симметричными углами.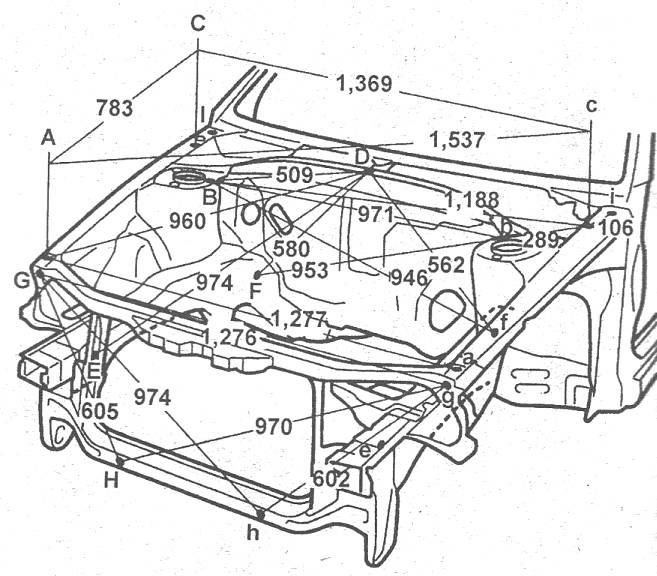
Контрольные точки располагаются в вертикальной или горизонтальной плоскостях. Их места варьируются в зависимости от модели машины. В руководствах по ремонту указывается местоположение конкретных точек и расстояния между ними.
Измерения производятся между центрами контрольных отверстий или между их краями.Обычно измеряются расстояния от центра до центра этих отверстий, расположенных в противоположных сторонах автомобиля. Отверстия контрольных точек обычно имеют больший диаметр, чем кончики измерительной линейки. В этом случае нужно делать измерение от края до края отверстий.
При необходимости измеряются места крепления элементов подвески, так как они влияют на развал-схождение. Можно также измерять положение колёс.
В случае аварийной деформации, контрольные точки можно использовать для определения центральной плоскости машины, опираясь на его неповреждённую часть. Далее центральная плоскость поможет узнать степень отклонения повреждённой части или правильность ремонта.
Далее центральная плоскость поможет узнать степень отклонения повреждённой части или правильность ремонта.
При использовании измерительной линейки, желательно иметь в наличии информацию о заводских параметрах расстояний между контрольными точками. Сверяясь с этими параметрами, нужно учитывать, какие расстояния указаны (от центра к центру или от края к краю). Если нет информации о заводских геометрических параметрах кузова, то можно использовать неповреждённый автомобиль той же модели для сравнения расстояний. Также используется сравнительное измерение противоположной, неповреждённой части.
Правила измерения геометрии кузова автомобиля
- Перед проверкой геометрии автомобиль должен стоять ровно. Колёса должны быть накачены с одинаковым давлением. В конструкции некоторых линеек присутствует уровень, для удобства расположения линейки параллельно плоскости машины.
 Это бывает необходимым, когда есть конкретные данные расстояний между контрольными точками для измерительной линейки. Нужно учитывать, что в некоторых руководствах по ремонту показаны расстояния для измерительной линейки (значениями на шкале линейки), а в других расстояния от точки к точке (фактическое расстояние). Это могут быть разные значения.
Это бывает необходимым, когда есть конкретные данные расстояний между контрольными точками для измерительной линейки. Нужно учитывать, что в некоторых руководствах по ремонту показаны расстояния для измерительной линейки (значениями на шкале линейки), а в других расстояния от точки к точке (фактическое расстояние). Это могут быть разные значения. - Таким образом, для правильного измерения, линейка должна располагаться параллельно кузову, иначе показания будут некорректными (опять же, если осуществляется сравнение с данными расстояний для её шкалы). Для этого иногда указатели линейки должны быть выдвинуты на разную длину. В этом случае показания на шкале линейки могут не совпадать с реальным расстоянием и требуют дополнительного замера рулеткой между указателями. Когда указатели выдвинуты на одинаковую длину, то значение на шкале совпадает с фактическим.

- Измерения делаются по фиксированным точкам кузова, таким как болты, разъёмы или отверстия и пр.
- Каждое измерение должно проверяться с помощью двух дополнительных контрольных точек.
- Лучше измерять более длинные расстояния. Так можно получить наиболее достоверную картину смещения структурных элементов.
- В некоторых случаях измерение и сравнение длины двух противоположных сторон дают лучшее представление о деформации, чем диагональные измерения. Нужно использовать диагональные замеры в совокупности с замерами длины.
- При измерении и ремонте разрешается определённый допуск (суммарный допуск не более 3 мм). Допуск в 3 мм был долгие годы разрешён при производстве автомобилей. В сегодняшние дни многие производители изготавливают кузова с нулевым допуском.
- Измерение расстояния между отверстиями одинакового диаметра делаются от центра к центру, либо от края к краю.
 Расстояние между креплениями делается от центра к центру (к примеру, между центрами головок болтов).
Расстояние между креплениями делается от центра к центру (к примеру, между центрами головок болтов). - Расстояние между отверстиями разного размера производится двумя измерениями. Первый замер делается между внутренними краями отверстий, второй делается между наружными краями отверстий. Далее два получившиеся значения суммируются и сумма делится на 2. Результатом будет расстояние между центрами отверстий разного размера.
Проверка геометрии кузова рулеткой
Рулетка используется, когда нет препятствий между измеряемыми точками. При измерении рулеткой нужно, чтобы лента не была изогнута. Смотреть на шкалу нужно только под углом 90 градусов и каждый раз с одинакового места, чтобы не ошибиться в значении. Нужно, чтобы фиксатор ленты не имел излишнего люфта. Лента рулетки должна лежать ровно между точками, чтобы измерение было корректным. Для удобства работы с небольшими отверстиями, фиксатор ленты можно доработать (см. рисунок).
Для удобства работы с небольшими отверстиями, фиксатор ленты можно доработать (см. рисунок).
Линейка для измерения геометрии кузова автомобиля
Раскладная измерительная линейка является наиболее часто применяемым устройством для проверки геометрии кузова.
Измерительная линейка способна мерить расстояние между двумя точками. Каждое расстояние должно проверяться двумя дополнительными контрольными точками.
Современная линейка для измерения геометрии кузова является телескопическим устройством с регулируемыми по высоте указателями. Даже при раскладывании на полную длину, она не даёт погрешности. В зависимости от типа используемой линейки может потребоваться дополнительный замер между указателями. К дополнительным аксессуарам относятся насадки и расширения для плотного размещения в отверстиях.
Линейка позволяет производить измерения при наличии препятствий между измеряемыми точками.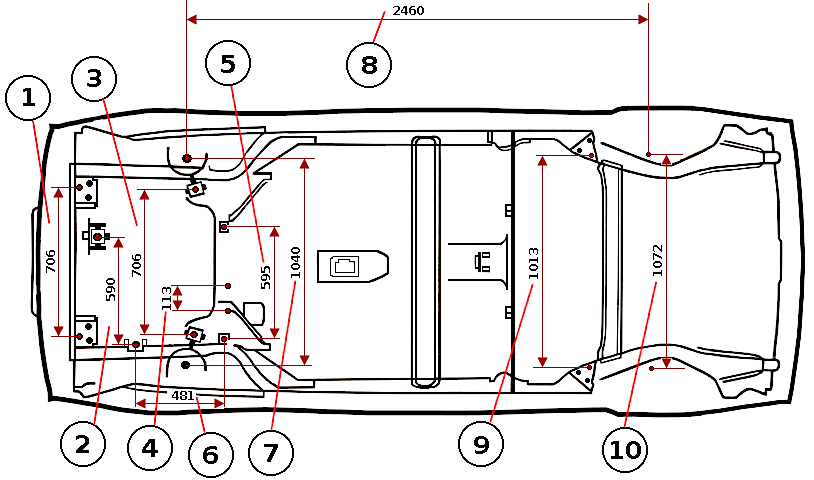
Все автомобили симметричны относительно воображаемой центральной плоскости, расположенной вдоль центра машины. Однако, бывает несколько точек на некоторых авто, которые, по разным причинам, не симметричны, но они не делают всю машину ассиметричной. Без симметрии автомобиль было бы очень сложно изготовить, да и продать.
Важно, чтобы указатели были плотно вставлены в отверстия.
Как было упомянуто ранее, если указатели были выставлены на разную высоту, то значение на шкале линейки может отличаться от фактического расстояния между измеряемыми точками. Для корректного значения нужно дополнительно мерить расстояние между указателями рулеткой.
Линейка и указатели должны быть ровными. Указатели должны располагаться на 90 градусов относительно линейки и не иметь люфта.
Важно, чтобы при измерении длина указателей была выставлена на одинаковом расстоянии.
Если не требуется получить точные значения, а производится сравнение одной стороны с другой, то линейка не обязательно должна располагаться параллельно плоскости машины. Можно сравнивать расстояния с противоположной частью, а также с подобными точками такого же целого авто.
Указатели не нужно надавливать при измерении, чтобы они не гнулись и показания не искажались. Данную линейку можно изготовить самому (см. статью).
В дополнение к диагональным измерениям необходимо делать замеры длины и ширины. Это даст более точное представление о правильности расположения контрольных точек. Диагональные измерения могут совпадать, даже если есть смещение обеих сторон.
Сравнительное измерение геометрии кузова автомобиля
Самый быстрый метод измерения повреждённой части кузова – сравнительное измерение. Для этих целей хорошо подходит специальный циркуль, но также можно использовать и измерительную линейку.
Циркуль для сравнительного измерения геометрии кузова
Циркуль для сравнительного измерения геометрии кузова напоминает по конструкции обычный циркуль. Два указателя соединены вместе и не имеют какой-либо шкалы. Для сравнительного замера необходимо каждый из указателей поместить в отверстие контрольных точек, расстояние между которыми необходимо проверить.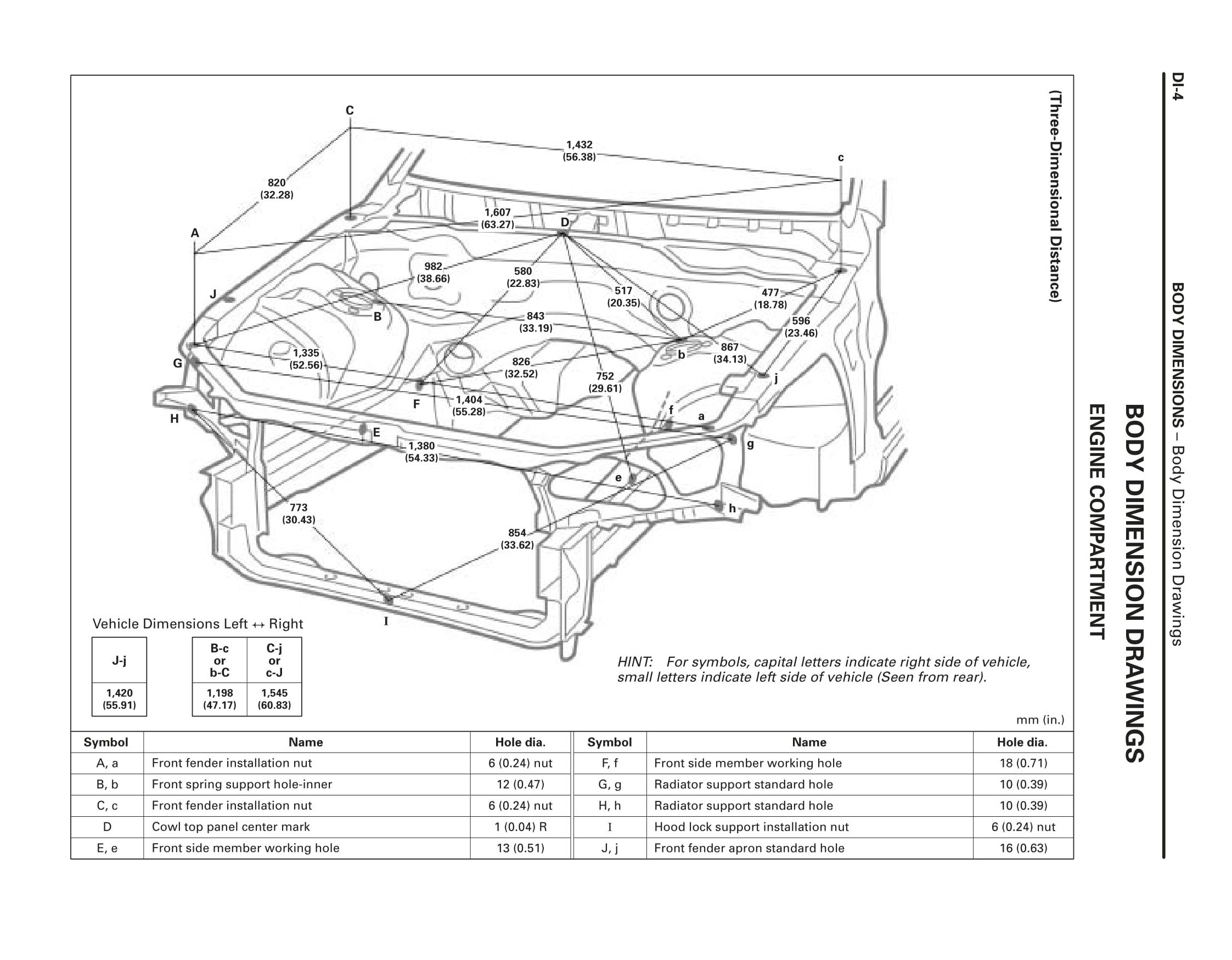
Трёхмерное измерение кузова автомобиля
Трёхмерное измерение включает в себя измерение длины, ширины и высоты структурных элементов кузова. Оно осуществляется трёхмерными измерительными системами.
Принцип таков, что при помощи измерительной системы получают расстояние от воображаемых основных плоскостей кузова: центральной, основной и нулевой (см. иллюстрацию).
Эти плоскости является воображаемыми. Такие плоскости устанавливаются и используются трёхмерной измерительной системой.
Ширина измеряется от центральной плоскости автомобиля, длина от нулевой плоскости, а высота от основной (расположенной параллельно днищу).
Центральная плоскость
Центральная плоскость или центральная линия делит автомобиль на две одинаковых половины вдоль. На некоторых машинах существуют метки, показывающие центр автомобиля. Такие метки отштампованы на металле кузова как в верхней, так и в нижней его части. Этим можно воспользоваться при замере простой измерительной линейкой или рулеткой. Они помогают сохранить время при проведении замеров. Расстояние от центра до конкретной точки справа будет таким же, что и расстояние от центральной линии к такой же точки слева. Большинство автомобилей сделаны симметричными за исключением некоторых точек.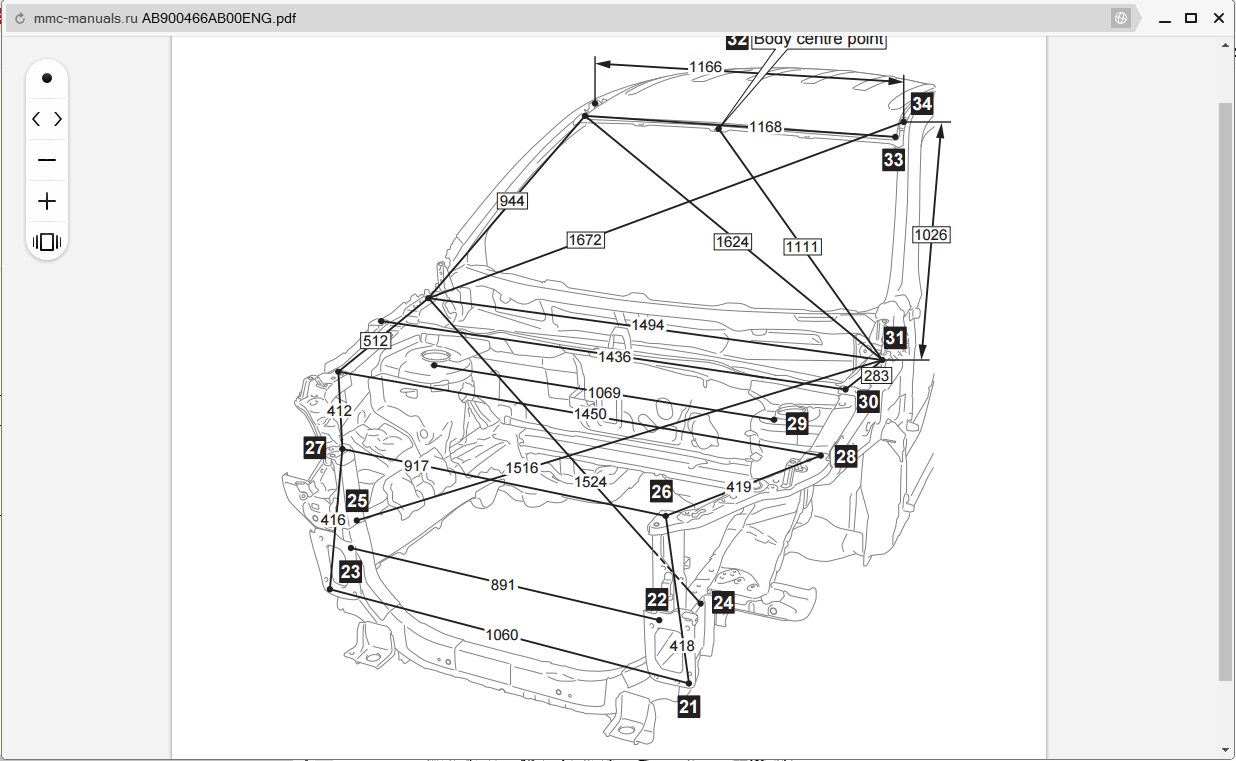 Одна часть кузова должна быть зеркальной противоположной стороне.
Одна часть кузова должна быть зеркальной противоположной стороне.
Измерение днища кузова
На днище производятся как диагональные измерения, так и проверка на скручивание и смещение относительно центральной линии.
Скручивание или смещение относительно центра можно проверить на центральной секции кузова.
Для такой проверки существует метод подвешивания центрирующих линеек в контрольные отверстия на днище. Места, на которые подвешиваются линейки, не должны быть деформированы. Подвешивается несколько линеек вдоль силовых элементов днища. Если они параллельны, то скручивания нет, если не параллельны, то скручивание присутствует. Центр линеек также должен совпадать, иначе существует смещение относительно центральной плоскости.
Печатать статью
Ещё интересные статьи:
Контрольные точки геометрии кузова ваз 2110
Контрольные точки геометрии кузова ВАЗ 2110, 2111, 2112
Автомобили, которые только что сошли с конвейера, имеют строго выверенные кузовные размеры. Имея под рукой эти размеры можно определить, попадал ли автомобиль в ДТП. Также контрольные размеры кузова пригодятся в случае ремонта и восстановительных работ после такой аварии. Имея под рукой эти размеры можно определить, попадал ли автомобиль в ДТП. Также контрольные размеры кузова пригодятся в случае ремонта и восстановительных работ после такой аварии. |
- вытяжкой;
- рихтовкой;
- правкой с усадкой металла;
- вырезкой участков, не поддающихся ремонту;
- изготовлением ремонтных вставок из выбракованных деталей кузова или листового металла с приданием им формы восстанавливаемой детали.

Деформированные места панелей выправляют, как правило, вручную при помощи специального инструмента (металлических, пластмассовых, деревянных молотков и различных оправок) и приспособлений. Правку с нагревом используют для осаживания (стягивания) сильно растянутых поверхностей панелей. Для предотвращения резкого вспучивания и ухудшения механических свойств панели нагревают до 600-650°С (вишнево-красный цвет). Диаметр нагретого пятна должен быть не более 20-30 мм.
Дополнительно можете скачать электронный документ в формате PDF «КУЗОВА АВТОМОБИЛЕЙ LADA, технические требования при приемке в ремонт, ремонте и выпуске из ремонта предприятиями сервисно-сбытовой сети ОАО АвтоВАЗ» (Пароль на архив: lada2111.ru).В этом руководстве можно найти:- Размеры проемов и зазоры сопрягаемых деталей кузова ВАЗ 2110, 2111, 2112 и 21123
- Точки крепления двигателя и подвесок на кузовах ВАЗ 2110, 2111, 2112
- Требования к окрашенной поверхности отремонтированного кузова
- Классификацию перекосов кузова
- и многое другое
 После восстановления геометрии кузова его необходимо покрасить. Читайте, как это сделать своими руками.
После восстановления геометрии кузова его необходимо покрасить. Читайте, как это сделать своими руками.Приходилось ли Вам пользоваться геометрическими размерами кузова ВАЗ? |
Интересный сайт? Поделись с друзьями
Геометрические размеры кузова Ваз 2110 согласно контрольным точкам
Геометрические размеры кузова Ваз 2110 и как их снимать»>
Как снимать кузовные размеры ваз 2110 по инструкцииГеометрические размеры могут нарушиться, если автомашина побывала в ДТП. Автокатастрофа может подразумевать крушение двух ТС, столкнувшихся вместе, наскок на препятствие или залет колеса в ямку. Из статьи вы узнаете, как проводится измерение геометрии кузова «десятки», какие методы позволяют дать точное заключение деформациям и повреждениям, а также многое другое.
Кузовная геометрия и ее диагностика
Важнейшие составляющие кузовной геометрии называются контрольными точками. Именно знание их месторасположения и умение грамотно измерять расстояния между ними, определяет структуру проверки кузова на деформации. О контрольных точках подробно можно узнать из техдокументации по каждой модели автомобиля.
О контрольных точках подробно можно узнать из техдокументации по каждой модели автомобиля.
Целостность кузова после определения повреждений, как правило, восстанавливают в специальных мастерских. Опытные рихтовщики в кратчайшие сроки приводят кузов в норму, если только деформации несут среднюю или незначительную степень тяжести. Кузов, побывавший в серьезной аварии и получивший много деформаций, как правило, легче заменить на новый.
Какие могут быть деформации на Ваз 2110
Ваз 2110 контрольные размеры кузова«Десятка», участвовавшая в аварии, будет иметь определенные отклонения от стандартных позиций, помеченных на заводе. И деструкции в данном случае подразумевают следующее:
- Отклонения в плане стандартного расположения колес, чему свидетельствует плохая устойчивость автомашины и увеличенный износ шин;
- Нарушаются диагонали, опять же, стандартно установленные на заводе. Особенно часто страдают дверные проемы, стойки и другие зоны кузова, так или иначе, сопряженные с зоной удара.

В большинстве случаев деструкция функциональных элементов сопрягается с появлением складок пола или других составляющих кузова. Кроме того, внешние удары вызывают существенное увеличение детали в дальних от места воздействия зонах.
Примечание. К таким, конструктивно слабым зонам, относятся пустые места между сварными швами, лонжероны и другие элементы, где наблюдается свободное взаимное движение металлических листов.
Несколько способов проверки кузова на деформации
Определить деформацию кузова, побывавшего в аварии средней тяжести, можно с первого взгляда. Напротив, если удар был слабый, то определить повреждения на глаз бывает крайне сложно. В этом случае приходится тщательным образом проводить диагностику, измерять соответствия и так далее.
Ваз 2110 геометрия кузова размеры и инструментГидравлический домкрат помогает осуществить первичный осмотр автомобиля. Благодаря подъемнику можно изучить состояние пола, прощупать те места кузова, которые недоступны для контроля при обычном расположении машины, на наличие складок. После обнаружения последних, как правило, их намечают маркером, что дает возможность легкого нахождения деформированных участков при последующих этапах работы.
После обнаружения последних, как правило, их намечают маркером, что дает возможность легкого нахождения деформированных участков при последующих этапах работы.
Если такая проверка не дает никаких результатов, переходят к следующему этапу обследования, подразумевающему проверку колес. Уже не домкрат, а специальный стенд помогает осуществить проверку. На таком оборудовании легко и быстрее проводить второй этап диагностики. Проверяют передние и задние колеса машины по контрольным точкам, используя штангенциркуль с особой формой профиля.
Геометрия и размеры кузова ваз 2110: измерительная установкаПроверка соответствия контрольных точек «обувки» автомобиля подразумевает верификацию (сравнение) колесных координат, расположенных по одну сторону машины с координатами на другой стороне. Деформация кузова становится очевидной, если измерения показывают значительные отклонения от заданных норм.
Еще одним методом диагностики кузова «десятки» на повреждения является сравнение диагоналей. Точные координаты основных диагоналей приведены ниже в таблице. Такая диагностика считается самой правильной, так как она осуществляется с помощью проверки симметрии.
Точные координаты основных диагоналей приведены ниже в таблице. Такая диагностика считается самой правильной, так как она осуществляется с помощью проверки симметрии.
Современные технологии позволяют осуществить с помощью различных инструментов. Хорошо помогает в этом деле компьютер, на котором проводятся соответствующие измерения. Используется также вариант проверки при помощи шаблонных инструментов и механических измерений.
Как правило, в домашних условиях на Ваз 2110 геометрические размеры кузова своими руками можно снять при помощи стандартной рулетки. А вот на СТО с этой же целью уже используется специальная телескопическая линейка, дающая более точные результаты.
Ваз 2110 размеры кузова и геометрияТолько вот оба этих способа измерения отличаются существенным недостатком. Так, они не дают возможность проведения измерения пространственных деформаций. Последние можно диагностировать только с помощью шаблонных или компьютерных методов. Это даст полную картину деформаций, что и позволит устранить повреждения наиболее эффективно. Хотя, цена такой проверки будет в разы выше.
Это даст полную картину деформаций, что и позволит устранить повреждения наиболее эффективно. Хотя, цена такой проверки будет в разы выше.
Кузов машины является замысловатой и сложной конструкцией, обладающей рядом обязательных для нормальной работы значений. Их нарушение вызывает существенные отклонения, изменяется конфигурация целостного кузова. Проводя измерения геометрии кузова, владелец автомобиля получает возможность обнаружить даже самые незначительные дефекты, могущие в дальнейшем привести к большим проблемам.
Геометрия кузова размеры ваз 2110Заводские габариты кузова Ваз 2110
| Длина | если взять конечные точки переднего и заднего бамперов, то здесь имеем 4265 мм; длина между центрами передних и задних колес, т.н. колесная база, составляет 2492 мм; от центра переднего колеса до крайней точки переднего бампера – 829 мм; от центра заднего колеса до конечной точки заднего бампера – 944 мм |
| Высота | 1420 мм |
| Ширина | спереди по крайним точкам «заводских» зеркал – 1875; спереди без учета зеркал (чисто «железо») – 1680 мм; расстояние между центрами передних колес – 1400 мм; задняя часть автомобиля имеет ширину между центрами колес 1370 мм |
Размеры диагоналей кузова Ваз 2110
| Диагональ проема передней двери от крайней точки порога снизу до верха стойки (длинная диагональ), мм | 1345 |
| Диагональ проема передней двери от крайней точки низа лобового окна до низа стойки двери (короткая диагональ), мм | 900 |
| Диагональ проема задней двери от крайней точки порога снизу до верха стойки (длинная диагональ), мм | 1040 |
| Диагональ проема передней двери от крайней точки низа заднего окна до низа стойки двери (короткая диагональ), мм | 1050 |
| Диагональ капота, мм | 1490 |
| Диагональ крышки багажника, мм | 1090 |
| Диагональ лобового окна, мм | 1365 |
| Диагональ заднего окна, мм | 1215 |
Несколько способов восстановления
кузова «десятки», в большинстве случаев, включает 6 видов работ следующего порядка:
- Диагностику кузова, его проверку на деформации и их характер, степень тяжести и так далее;
- Работы, направленные на устранение поверхностных повреждений.
 Их еще называют жестяными работами;
Их еще называют жестяными работами; - Правку и вытягивание деформированных деталей, включающую наличие специального оборудования, такого как стапель;
- Удаление слишком поврежденный составляющих кузова и его навесных деталей;
- Замену частей кузова на оригинальные элементы;
- Покраску и восстановление ЛКП.
В этом видео можно посмотреть, как вытягивается деталь кузова при помощи стапеля.
Кузовные особенности «десятки»
Ваз 2110 или просто «десятка» оснащена кузовом несущей конструкции. Это 4-дверный седан переднеприводного типа, перенявший от своего предшественника Ваз 21099 некоторые особенности.
Примечание. Это вовсе не означает, что «десятка» не имеет индивидуальных черт. Напротив, как и любое творение вазовского автопрома, модель отличается набором характеристик, присущим только ей.
Контрольные размеры кузова ваз 2110По сути, Ваз 2110 прочили, как модификацию «восьмерки» еще в 1983-м году. В дальнейшем эту базу использовали уже для изготовления и выпуска совершенно нового автомобиля. Пока же конструкторы решили модифицировать Ваз 2108 в 21099, оставив идею создания Ваз 2110 на будущее.
В дальнейшем эту базу использовали уже для изготовления и выпуска совершенно нового автомобиля. Пока же конструкторы решили модифицировать Ваз 2108 в 21099, оставив идею создания Ваз 2110 на будущее.
Примечание. По слухам, тогдашние работы по созданию «десятки» требовали больших изменений в конструкции и устройстве кузова, что неминуемо приводило к удорожанию. В то время АвтоВаз был к этому пока не готов.
Попадает «десятка» в серийное производство лишь в 1991-м году. Выпуск нового седана, не имеющего в отличие от своих родичей, как ни странно, собственного названия, продолжили на ВАЗ в 1995 году. Тремя годами позже наладили производство универсала.
Примечание. Ваз 2110 на тот момент – это единственная модель, кузов которой реализовали тремя способами.
К 1996-у году Ваз 2110 утрачивает свою популярность, что можно объяснить значительным прогрессом в мировом автомобилестроении. Современная и прогрессивная когда-то в плане технологичности машина в лице Ваз 2110 перестает быть таковой, утрачивает свою привлекательность. Хотя, с другой стороны, этого не сказали бы в то время про седан, который неплохо покупается и по сей день.
Хотя, с другой стороны, этого не сказали бы в то время про седан, который неплохо покупается и по сей день.
Именно с 1996 года «десятку» стали выпускать серийно в кузове типа седан. Конструкторы модернизировали целый ряд кузовных элементов, внесли различные новшества. К примеру, одним из нововведений можно назвать внедрение газовых упоров в капот автомобиля.
Ваз 2110 считался на то время дорогим автомобилем. И это неудивительно, ведь инженеры отечественного автопрома старались модернизировать этот автомобиль как можно лучше. Они даже предусмотрели возможность монтажа кондиционера в салон. Багажник вообще получился на загляденье – большой и вместительный.
Правда, с универсалом в плане вместительности багажного отсека седан тягаться не мог, но этого нельзя сказать относительно удобства пользования. Так, из-за неудачной конструкции, петли на универсале забирали немалую часть полезного объема багажника. Кроме того, неудобство загрузки в багажник универсала вещей добавляли чересчур раздутые колесные ниши.
В седане, напротив, багажник устроен хорошо. Особенно ярко выделяется место под запаску. Колесный диск можно ставить сюда в перевернутом виде, что позволяет загружать компактно различные вещи и инструменты в еще одно свободное пространство.
Что касается очередной модификации «десятки» под названием Ваз Премьер, то она – точная копия Ваз 2110, только с удлиненным кузовом. Производство этой модели подразумевало использование оригинального комплекта кузовных деталей. Они не подходят к корпусу седана. К тому же, проектируя кузов Премьер, инженеры позаботились о придании ему дополнительной жесткости.
Усилению был подвергнут в первую очередь пол. Модернизирована подвеска, обладающая большей жесткостью, чем седановская. Общий вес автомобиля увеличился на 65 кг. Что касается покраски, то она проводилась также, как и на Ваз 2110 седан.
Надеемся, что информация, приведенная в статье, поможет в конкретной ситуации. Если проверка геометрии и ее восстановление будет проводиться своими руками, рекомендуем тщательно изучить фото и видео.
Геометрические размеры кузова ВАЗ 2110.
Примеры карт геометрических размеров уменьшены для примера. Скачиваемый файл PDF. Файлы хранятся на Яндекс диске.
Заводские размеры по ГОСТ — 2.104-68. Книга содержит 38 страниц, в том числе Нива, Гранта, Нива-Шевроле, Ока, Калина, Надежда. Необходимые технические параметры для восстановления и ремонта.
Модель: ВАЗ 2110, 2111, 2112. Контрольные точки геометрии кузова. Дверные проемы, под капотные, низ кузова, самые полные размеры. СКАЧАТЬ Модель: ВАЗ 2110, 2111, 2112. Контрольные точки геометрии кузова. Дверные проемы, под капотные, низ кузова, самые полные размеры. СКАЧАТЬЦветное иллюстрированное руководство по самостоятельному тюнингу автомобиля ВАЗ 2110 и его модификаций. В книге подробно описаны тюнинговые работы по усовершенствованию конструкции автомобилей семейства ВАЗ-2110. Все операции по тюнингу двигателя, трансмиссии, ходовой части, а также оборудования кузова проиллюстрированы и снабжены подробными комментариями и рекомендациями.
Размер файла: 20.17 Mb.
СКАЧАТЬГеометрия ВАЗ 2110
22-01-2015, 17:03, посмотрело: 69732
Геометрические размеры кузова ВАЗ 2110, данные по геометрии кузова и контрольным точкам Ваз 2110 из различных ремонтных баз и заводских сервис мануалов.Скачать Геометрические размеры кузова ВАЗ 2110
Стоимость скачивания файла: 10.00 usd Ссылка будет доступна в течении 16 ч. после оплаты После оплаты на указанный емейл будет выслана ссылка на скачивание файла, либо вы можете
повторно нажать кнопку ‘Купить’ и загрузка файла начнется автоматически.
Уважаемый посетитель, Вы зашли на сайт как незарегистрированный пользователь. Мы рекомендуем Вам зарегистрироваться либо войти на сайт под своим именем.Контрольные точки геометрии кузова ВАЗ 2110, 2111, 2112
Значительная часть ремонтных работ по автомобилям, особенно поступающим после дорожно-транспортных происшествий, приходится на ремонт кузовов. В большинстве случаев при ремонте кузова требуется проверка геометрии точек крепления узлов и агрегатов шасси автомобиля.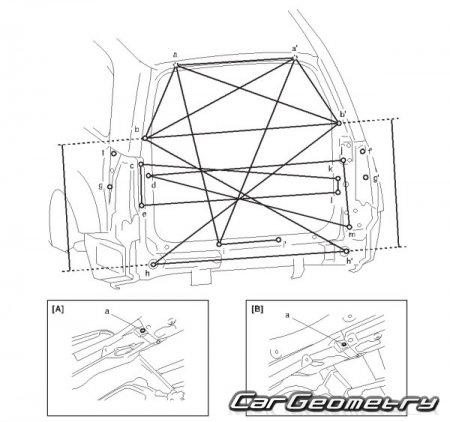 Геометрия кузова и моторного отсека ВАЗ 2110-12 на схемах:
Геометрия кузова и моторного отсека ВАЗ 2110-12 на схемах:
Если кузов сильно поврежден, рекомендуется снимать все внутренние обивочные детали, чтобы облегчить измерение, контроль и установку гидравлических и винтовых домкратов для устранения перекосов и повреждений кузова.
Выступание лицевых поверхностей и съемных деталей относительно соседних панелей, устраняется их подгонкой и регулировкой.
- вытяжкой;
- рихтовкой;
- правкой с усадкой металла;
- вырезкой участков, не поддающихся ремонту;
- изготовлением ремонтных вставок из выбракованных деталей кузова или листового металла с приданием им формы восстанавливаемой детали.
Деформированные места панелей выправляют, как правило, вручную при помощи специального инструмента (металлических, пластмассовых, деревянных молотков и различных оправок) и приспособлений. Правку с нагревом используют для осаживания (стягивания) сильно растянутых поверхностей панелей. Для предотвращения резкого вспучивания и ухудшения механических свойств панели нагревают до 600-650°С (вишнево-красный цвет). Диаметр нагретого пятна должен быть не более 20-30 мм.
Диаметр нагретого пятна должен быть не более 20-30 мм.
Дополнительно можете скачать электронный документ в формате PDF «КУЗОВА АВТОМОБИЛЕЙ LADA, технические требования при приемке в ремонт, ремонте и выпуске из ремонта предприятиями сервисно-сбытовой сети ОАО АвтоВАЗ» (Пароль на архив: lada2111.ru).
- Размеры проемов и зазоры сопрягаемых деталей кузова ВАЗ 2110, 2111, 2112 и 21123
- Точки крепления двигателя и подвесок на кузовах ВАЗ 2110, 2111, 2112
- Требования к окрашенной поверхности отремонтированного кузова
- Классификацию перекосов кузова
- и многое другое
Приходилось ли Вам пользоваться геометрическими размерами кузова ВАЗ?
Комментарии
Пожалуйста, соблюдайте простые правила:
1. Не оскорбляйте чужое достоинство;
2. Не употребляйте ненормативную лексику, проще говоря мат;
3. Реклама запрещена;
Реклама запрещена;
4. Не добавлять комментарии бессодержательного характера (флуд)
Копирование материала разрешается только с указанием ссылки на источник.
Материалы: http://xn--2111-43da1a8c.xn--p1ai/spravka/1317-control-psets-geometry-kuzov-vaz-2110-2111-2112.html
автомобилей ваз 2110 — 2112
1 — облицовка рамки радиатора; 2 — рамка радиатора; 3 — верхняя поперечина рамки радиатора; 4 — правое переднее крыло; 5 — щиток передка; 6 — петля капота; 7 — капот; 8 — правая передняя дверь; 9 — стойка ветрового окна; 10 — внутренняя панель передней двери; 11 — внутренняя панель задней двери; 12 — правая задняя дверь; 13 — рамка люка крыши; 14 — левая боковина; 15 — панель крыши; 16 — опора пружины задней подвески; 17 — крышка багажника; 18 — внутренняя панель крышки багажника; 19 — рамка окна боковины; 20 — задний бампер; 21 — задняя стойка; 22 — левая задняя дверь; 23 — арка заднего колеса; 24 — средний пол; 25 — ниша запасного колеса; 26 — центральная стойка; 27 — левая передняя дверь; 28 — передняя стойка; 29 — передний пол; 30 — левое переднее крыло; 31 — опора пружины передней подвески; 32 — кронштейн; 33 — передний лонжерон; 34 — кронштейн проушины для буксировки; 35 — панель передка; 36 — передний бампер
Ремонт поврежденного кузова ваз 2110 Значительная часть ремонтных работ по автомобилям, особенно поступающим после дорожно-транспортных происшествий, приходится на ремонт кузовов.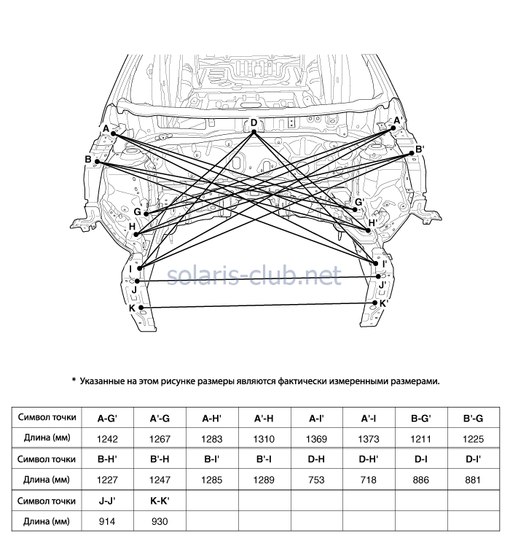 В большинстве случаев при ремонте кузова требуется проверка геометрии точек крепления узлов и агрегатов шасси автомобиля. Основные справочные размеры кузова ваз 2110 для проверки показаны на рис. 8-4.
В большинстве случаев при ремонте кузова требуется проверка геометрии точек крепления узлов и агрегатов шасси автомобиля. Основные справочные размеры кузова ваз 2110 для проверки показаны на рис. 8-4.
Повреждения кузова автомобилей ваз 2110 могут быть самыми различными. Поэтому правила ремонта в каждом отдельном случае должны быть свои, наиболее подходящие для этих повреждений, при этом необходимо максимально использовать возможности рихтовки поврежденных панелей. По возможности необходимо избегать термического воздействия на металл, чтобы не нарушать заводскую сварку и противокоррозионную защиту кузова. Лицевые панели кузова ваз 2110 следует снимать только в крайних случаях, чтобы определить места повреждений, выправить или выверить кузов.
В случаях значительных повреждений кузова автомобиля ваз 2110 рекомендуется снимать все внутренние обивочные детали, чтобы облегчить измерение, контроль и установку гидравлических и винтовых домкратов для устранения перекосов и повреждений кузова.
Выступание лицевых поверхностей и съемных деталей относительно соседних панелей, устраняется их подгонкой и регулировкой.
X, У, Z — базовые линии; 1 — верхнего крепления радиатора; 2 — поперечины передней подвески к рамке радиатора; 3 — рычагов передней подвески; 4 — правой опоры силового агрегата; 5 — левой опоры силового агрегата; 6 — базовые точки; 7 — верхней штанги подвески силового агрегата; 8 — базовые отверстия; 9 — задней подвески силового агрегата; 10 — рычага переключений передач; 11 — регулятора тормозов; 12 — рычагов задней подвески; 13 — верхних точек крепления стоек задней подвески; 14 — базовые отверстия
Деформированные места панелей выправляют, как правило, вручную при помощи специального инструмента (металлических, пластмассовых, деревянных молотков и различных оправок) и приспособлений.
Правку с нагревом используют для осаживания (стягивания) сильно растянутых поверхностей панелей. Для предотвращения резкого вспучивания и ухудшения механических свойств панели нагревают до 600-650°С (вишнево-красный цвет). Диаметр нагретого пятна должен быть не более 20-30 мм.
Диаметр нагретого пятна должен быть не более 20-30 мм.
Стягивание поверхностей производите следующим образом:
угольным электродом сварочного полуавтомата или газовой горелкой нагрейте металл от периферии к центру дефектного участка и ударами деревянной киянки и молотка осаживайте нагретые места, используя плоскую поддержку или наковальню;
повторяйте операции нагревания и осаживания до получения необходимой поверхности панели.
Неровности на панелях можно выровнять при помощи полиэфирных шпатлевок, термопластика, эпоксидных мастик холодного отвердения и при помощи припоя.
Полиэфирные шпатлевки типа «Хемпропол-П» или «ПЭ-0085» образуют надежные соединения с панелями, зачищенными до металла. Они представляют собой двухкомпонентные материалы: ненасыщенную полиэфирную смолу и отвердитель, который является катализатором быстрого отвердения смеси. Температура в рабочем помещении не должна быть ниже 18°С. Приготовленную полиэфирную шпатлевку необходимо использовать по времени не более чем за 10 мин.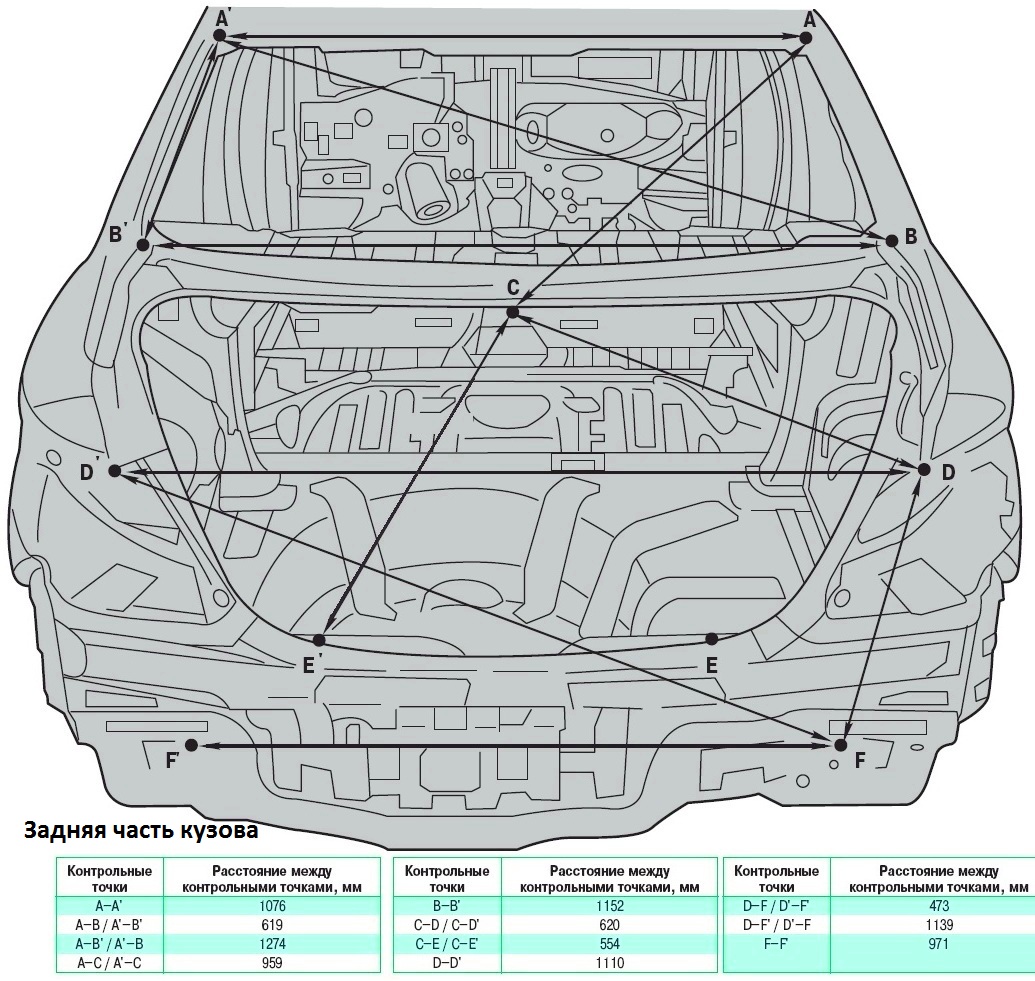 Она окончательно затвердевает через 60 мин после нанесения. Толщина слоя шпатлевки не должна превышать 2 мм.
Она окончательно затвердевает через 60 мин после нанесения. Толщина слоя шпатлевки не должна превышать 2 мм.
Термопластик выпускается в виде порошка. Эластичные свойства, необходимые для нанесения его на металлическую поверхность панели, приобретает при температуре 150-160°С. Поверхность, подлежащая заполнению, должна быть тщательно очищена от ржавчины, окалины, старой краски и других загрязнений. Адгезия термопластика лучше к шероховатой поверхности металла.
Для нанесения термопластика участок, подлежащий выравниванию, нагревают до 170-180°С и наносят первый слой порошка, который укатывают металлическим катком. Затем наносят второй слой и так далее до заполнения неровности. Каждый слой укатывают до получения монолитного слоя пластической массы. После отвердения слой обрабатывают обычными методами.
Припои типа ПОССу 18-2 или ПОССу 25-2 применяются для выравнивания участков, ранее заполненных припоем, наращивания кромок деталей и устранения зазоров.
При значительных повреждениях панели заменяют новыми с использованием электросварки в среде защитных газов.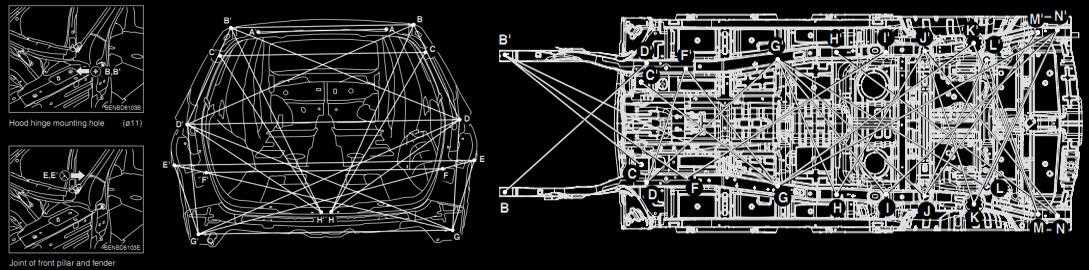
Осторожно отсоедините крыло и снимите изолирующие прокладки с мест контакта крыла с брызговиком. Снимите с крыла указатель поворота.
Установку крыла на автомобиль ваз 2110 выполняйте в обратной последовательности. Изолирующие прокладки рекомендуется устанавливать новые. Перед окончательным затягиванием винтов за счет увеличенных отверстий подгоните крыло по зазорам и выступанию с другими элементами кузова.
После замены крыла нанесите противокоррозионное покрытие на его внутреннюю поверхность. рис.8-5. Снятие переднего крыла
Материалы: http://car-exotic.com/vaz-cars/vaz-2110-car-body-2.html
Сходящие с конвейера автомобили имеют строго выверенные кузовные размеры. Как правило, при покупке нового автомобиля на это особого внимания никто не обращает.
Однако потребность измерять и сверять с руководством по эксплуатации геометрические размеры кузова у ВАЗ 2110 может возникнуть в таких случаях:
- вы покупаете автомобиль с рук, и не уверены в том, что он не побывал в аварии.
 Именно из-за этого, как правило, чаще всего нарушается геометрия ВАЗ 2110;
Именно из-за этого, как правило, чаще всего нарушается геометрия ВАЗ 2110; - вы сами попали в аварию, даже налетели на камень, бордюр и т.п., от чего машина получила серьезный удар.
Основные справочные размеры точек крепления узлов и агрегатов
- 1 Заводские габариты
- 2 Визуальная проверка
- 3 Инструментальная проверка по контрольным точкам
- 4 Тонкости кузовного ремонта
Все линейные размеры кузова ВАЗ 2110 можно найти, полистав книжку по эксплуатации или «порывшись» в интернете.
Но главные габариты таковы:
- если взять конечные точки переднего и заднего бамперов, то здесь имеем 4265 мм;
- длина между центрами передних и задних колес, т.н. колесная база, составляет 2492 мм;
- от центра переднего колеса до крайней точки переднего бампера – 829 мм;
- от центра заднего колеса до конечной точки заднего бампера – 944 мм.
Высота ВАЗ 2110 – 1420 мм.
Заводские габариты по длине и ширине
- спереди по крайним точкам «заводских» зеркал – 1875;
- спереди без учета зеркал (чисто «железо») – 1680 мм;
- расстояние между центрами передних колес – 1400 мм;
- задняя часть автомобиля имеет ширину между центрами колес 1370 мм.

Как проверить, что у ВАЗ 2110 все в порядке с геометрией кузова? Для визуального определения есть два метода, которые желательно применять оба:
Размеры проемов и зазоры сопрягаемых деталей
И все же, далеко не всегда все так просто. И даже опытный глаз не всегда заметит маленькие «несоответствия». При грамотном ремонте кузова геометрические размеры можно проверить, только произведя замеры. Профессионалы для этого используют специальные измерители.
Но для проведения данной процедуры в домашних условиях достаточно обычной рулетки. Нужно найти специальные контрольные отметки, которые находятся на днище ВАЗовского кузова. Именно от них следует производить замеры. Как и в какой последовательности – можно узнать из эксплуатационной инструкции к ВАЗ 2110.
Нужно найти специальные контрольные отметки, которые находятся на днище ВАЗовского кузова. Именно от них следует производить замеры. Как и в какой последовательности – можно узнать из эксплуатационной инструкции к ВАЗ 2110.
Если же, скажем, вам нужно убедиться, что линейные размеры именно вашей машины (например, вы меняли крылья, дверь и т.п.) совпадают, то не всегда следует доверять даже инструкции по эксплуатации, там тоже иногда можно найти ошибки.
Как контрольные габариты кузова используйте самолично снятые размеры с той стороны автомобиля, где никаких замен и рихтовок не проводилось.
Контрольные точки на кузове и днище
Снимать размеры необходимо по следующим точкам:
 Совпадают? Отлично, но на этом останавливаться не стоит;
Совпадают? Отлично, но на этом останавливаться не стоит;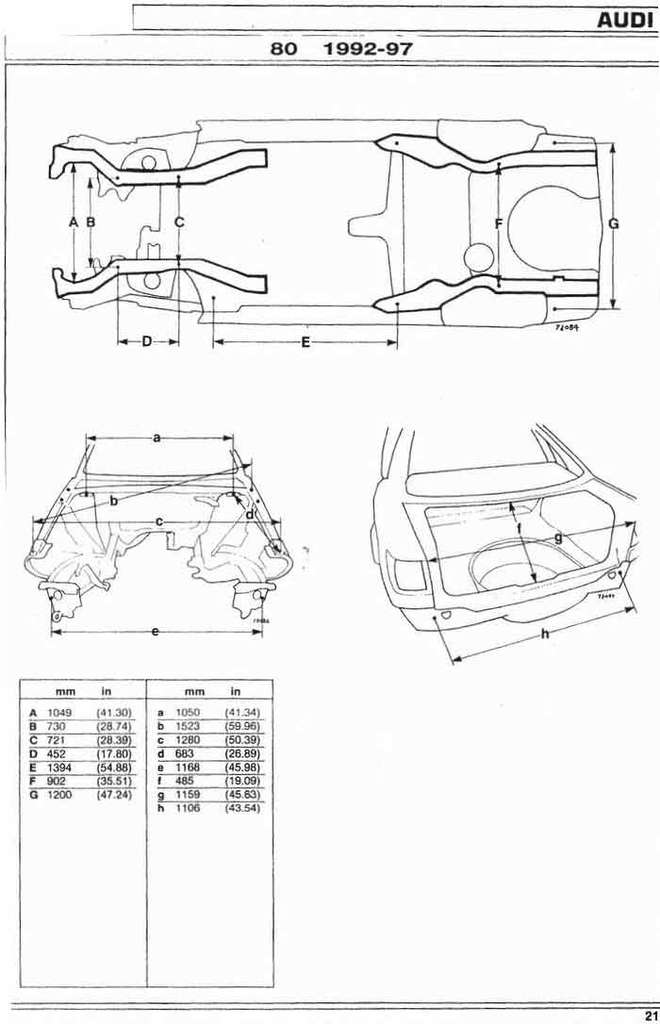
Ремонт кузова чаще всего проводится именно после ДТП, но также и в том случае, если какие-то детали проржавели. Но все же нужно стараться избегать сварочных и других работ, подразумевающих термическое нагревание металла.
По возможности старайтесь не снимать лицевых панелей. Это также может привести к изменению кузовной геометрии. И после любых ремонтных работ, связанных с кузовом, обязательно проверяйте его линейные размеры.
Материалы: http://hitmind.ru/488-gabaritnye-i-geometricheskie-razmery-kuzova-vaz-2110.html
Как проверить геометрию кузова автомобиля
Перед покупкой подержанного автомобиля важно суметь грамотно проверить (рассчитать) контрольные точки геометрии кузова. Если этого не сделать, можно получить во владение средство с деформированными кузовными элементами. На такой машине ездить очень опасно, так как снижается её пассивная безопасность, ухудшается управляемость, изменяются рабочие свойства.
Зачем проверять геометрию кузова автомобиля
Геометрическая диагностика является основной процедурой, которую рекомендуют проводить перед выбором автомобиля с вторичного рынка. Это позволяет узнать состояние машины — не попадала ли она в ДТП, как эксплуатировалась, как проверялась, проводился ли текущий ремонт.
Дополнительная причина — проверка уровня проведения рихтовки бампера, капота, крыши или другой части кузова. После столкновения автомобиль восстанавливается в сервисах. Однако мало кто из владельцев уделяет внимание качеству обслуживания, недостаткам. Со своей стороны, каждая третья СТО в Москве предлагает услугу проверки геометрии раз в 6 месяцев. Такие рекомендации являются вполне оправданными, учитывая состояние нынешних российских дорог.
Машина на стапеле для диагностики геометрии кузова
Геометрия кузова автомобиля — это система изначальной дислокации проверочных точек между собой. Её устанавливает производитель на стадии проектирования, выпуска транспортного средства. Таким образом, это точнейшая экспозиция панелей. Благодаря такой схеме гарантируется слаженная работа всех узлов, агрегатов автомобиля.
Таким образом, это точнейшая экспозиция панелей. Благодаря такой схеме гарантируется слаженная работа всех узлов, агрегатов автомобиля.
Наиболее важными считаются расстояния между самыми удалёнными точками панелей, несущих агрегаты ходовой части. Имеются в виду лонжероны, балки, подрамники, брызговики.
Тем самым, геометрия влияет на колёсную базу авто, размер колёс, а также другие характеристики, обеспечивающие безопасное и комфортное передвижение.
Причины и признаки нарушения
Кузовная геометрия может нарушиться не только после аварии. Вот несколько примеров, почему такое происходит: неровное дорожное полотно, высокая скорость езды, преграды на асфальте.
От конкретного фактора зависит и сила воздействия на панели, степень повреждения. Например, при наездах на «лежачие полицейские», корпус авто получает незначительные удары. Однако частые столкновения с барьерами со временем приводят к ощутимым изменениям, что подтверждается проверками.
Нарушение геометрии кузова заметно по различным признакам. При наличии следующих симптомов, надо поскорее отвезти машину на профессиональную диагностику:
- плохо закрывается капот, багажник, двери — при условии, что петли находятся в нормальном состоянии;
- машину уводит в сторону по трассе, она «рыскает» и вибрирует на высоких скоростях — при этом не наблюдается никаких проблем с элементами подвески.
Как определить (проверить) смещение знают только специалисты, разбирающиеся в конструкции определённой марки и модели автомобиля.
Как проверить геометрию кузова автомобиля
Проверка геометрии кузова возможна несколькими различными способами. Машина ставится обязательно ровно, воздух в колёсах — доводится до нормальных пределов (стандартные заводские значения). Замеры проводятся на основании неизменных точек остова (предпочтительно самых удалённых), с использованием не менее двух вспомогательных контрольных отверстий. Это даёт возможность получить наиболее достоверную картину смещения.
Это даёт возможность получить наиболее достоверную картину смещения.
Проверка контрольных точек на кузове
Визуально
Подобным методом сначала проверяют стёкла. Если на них имеются горизонтальные трещины, это один из явных признаков нарушения. После этого специалист приседает на корточки, осматривая борта — продольную часть машины. Таким способом лучше выявляются все зазоры и неровности, образовавшиеся между панелями. Очевидно, что визуально оценить корпус способен только мастер. Неопытный человек, даже при большом желании ничего обнаружить не сумеет.
Рулеткой
Как проверить кузов рулеткой — сначала находят заводские данные по удалённым контрольным точкам. При выполнении расчётов обязательно учитывают их диаметр, чтобы правильно провести измерение — беря за основу середину или крайние части отверстий. Если штатные величины геометрии отсутствуют, в качестве эталона используют параметры такого же автомобиля, только неповреждённого.
Инструментами
Безусловно, одним из эффективных инструментов для замера проверочных точек помимо линейки является уровень. Им оснащаются также некоторые измерительные рулетки, позволяющие одновременно диагностировать состояние плоскостей автомобиля. Также замеры осуществляются штангенциркулем и масштабной телескопической рейкой. Первый инструмент вычисляет правильность расположения колёс относительно друг друга, а второй — проверяет наличие деформации кузова.
Им оснащаются также некоторые измерительные рулетки, позволяющие одновременно диагностировать состояние плоскостей автомобиля. Также замеры осуществляются штангенциркулем и масштабной телескопической рейкой. Первый инструмент вычисляет правильность расположения колёс относительно друг друга, а второй — проверяет наличие деформации кузова.
В автосервисе
Однако какими идеальными не были инструменты, до качества стационарного оборудования им далеко.
В специализированных центрах применяют компьютеры, точно рассчитывающие малейшее смещение панелей по электронным датчикам.
Показания передаются на большой экран, где создаётся трёхмерная модель и данные сравниваются со штатными величинами. Таким способом удаётся выявить дефекты с 99-процентной точностью.
Что значат контрольные точки геометрии кузова
Контрольные мерки нужны для правильного измерения геометрии. Большая их часть — это технологические отверстия. Находятся они в тех или иных частях кузова. Часто в такой роли выступают базовые структурные элементы: рамка радиатора, фартуки, брызговики, днище, рамка номера. Главное — они должны находиться в горизонтальной или вертикальной плоскости.
Находятся они в тех или иных частях кузова. Часто в такой роли выступают базовые структурные элементы: рамка радиатора, фартуки, брызговики, днище, рамка номера. Главное — они должны находиться в горизонтальной или вертикальной плоскости.
Обычно при проверке геометрии за основу берут центры контрольных точек. Однако это касается только мелких, средних отверстий. Если же диаметр их чересчур большой, мерилом выступают крайние части. В некоторых случаях измеряют расстояние между апексами крепления элементов подвески, которые влияют на показатели развала-схождения. Для получения более точного результата возможна также фиксация углов положения колёс.
Схема контрольных точек и углов геометрии кузова автомобиля
Если кузов автомобиля после ДТП сильно деформировался, в качестве точек используют неповреждённые части автомобиля. Отталкиваясь от ровной плоскости, специалисты быстрее выявляют несоответствия, отклонения. Длина замеряется между отметками, находящимися на диаметральных зонах машины.
Эксплуатация автомобиля с нарушенной геометрией: возможные последствия
Эксплуатировать машину со смещённым корпусом опасно! Касается это повреждения лонжеронов, балки, рам, подрамников. Кроме того, что это повышает ежедневный расход владения машиной, приводя к увеличению потребления горючего, ещё существенно влияет на безопасность.
Если по кузову есть недочеты, это приводит к неравномерному износу шин. Объясняется такая ситуация тем, что шасси крепится к интегрированному силовому каркасу. Корпус, таким образом, задаёт точность расположения узлов ходовой части машины. После серьёзной аварии точки отклоняются от стандарта, что не позволяет выставить правильные углы схода/развала.
Как восстановить геометрию кузова
А возможно ли самостоятельное восстановление — ни в коем случае. Ремонт под силу только опытным кузовщикам. Если при диагностике выявляются нарушения, исправления дефектов возможно только на специальном стенде. После окончания ремонта специалист на компьютере измерит соответствие по всем точкам, отвечающим нормам производителя.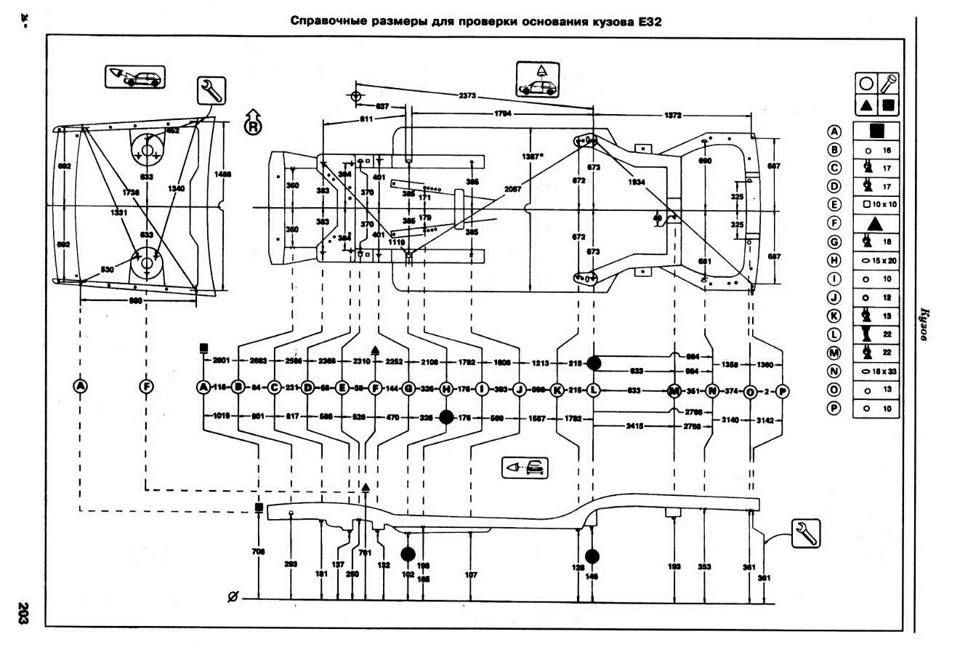
Цена проверки смещения кузовных панелей в автосервисе зависит от обширности нанесённого урона и конструкции конкретной модели ТС. Есть машины, где существуют скрытые точки, до которых невозможно добраться без сложной разборки двигателя, коробки. Такая операция занимает больше времени, поэтому стоимость работ автоматически увеличивается.
Контрольные размеры геометрии кузова Lada Largus / Лада Ларгус
См. также Габаритные размеры, Внутренние размеры салона и багажника, Зазоры и сечения деталей
Размеры проемов и зазоры сопрягаемых деталей кузова LARGUS
| А | Б | В | Г | Д | Е | Ж | 3 |
| 1380 ± 5 | 930 ± 4 | 1280 ± 5 | 1155 ± 15 | 925 ± 5 | 975 ± 5 | 1110 ± 5 | 610 ± 3 |
| И | К | Л | М | Н | О | П | |
| 795 ± 3 | 735 ± 3 | 1530 ± 5 | 800 ± 5 | 1380 ± 4 | 1030 ± 3 | 1140 ± 3 |
Точки крепления подвесок на кузове
1 — точки переднего крепления подрамника; 2 — точки крепления амортизаторной стойки; 3 — точки заднего крепления подрамника; 4 — направляющие отверстия переднего лонжерона; 5 — передние направляющие заднего лонжерона; 6 — направляющие отверстия крепления задней подвески; 7 — отверстия крепления задней подвески; 8 -отверстия крепления заднего амортизатора; 9 — задние направляющие отверстия заднего лонжерона.
Схема замера межосевых размеров
Перед:
-1: (В1) — (G2) = (В2) — (G1)
-2: (G1) — (С2) = (G2) — (С1)
Зад:
-1: (G2) — (В1) = (G1) — (В2)
-2 :(B1) — (J2) = (B2) — (J1)
Контрольные точки
Точка B1, B2
Точка G1, G2
Точка С1, С2
Точка J1, J2
Контрольные размеры и точки кузова Нива Шевроле
Основные справочные размеры точек крепления узлов и агрегатов автомобиля
1 — отверстия для установки радиатора; 2 — базовые отверстия 20 мм; 3 — крепления рулевого механизма; 4 — привалочная плоскость кронштейна маятникового рычага; 5 — крепления стабилизатора; 6 — крепления задней опоры силового агрегата; 7 — крепления раздаточной коробки; 8 — крепления рычагов задней подвески; 9 — крепления заднего амортизатора; 10 — базовое отверстие; 11 —крепления поперечной штанги; 12— привалочная плоскость рулевого механизма.
Размеры проёмов и зазоров
| А | Б | В | Г | Д | Е | Ж |
| 1440±5 | 1040±5 | 930±4 | 940±4 | 1285±5 | 816±4 | 540±2 |
| 3 | И | К | Л | М | Н | |
| 480±2 | 1480±5 | 1520±5 | 770±4 | 1420±5 | 920±4 |
Точки крепления и основные размеры для контроля
1,3-точки крепления передней подвески; 2 — базовые отверстия диаметром 20 мм; 4 — точки крепления стабилизатора; 5 — точки крепления задней опоры силового агрегата; 6 — передняя точка крепления раздаточной коробки; 7 — точки крепления нижних рычагов задней подвески; 8 — ось крепления верхних рычагов задней подвески; 9 — точки крепления заднего амортизатора; 10 — точка крепления поперечной штанги и базовое отверстие диаметром 20 мм
Видео
youtube.com/embed/-NhH0n7cz_0″ frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»/>
Контрольные точки кузова автомобилей Приора, Пежо 605, 2110, 2106 и их важное значение
Контрольные точки остова Приоры
Геометрию кузова своего автомобиля проверять крайне важно. Многие эксплуатируют машину годами, даже не подозревая про такое понятие, как замеры. Главную роль в измерении геометрии играют, безусловно, контрольные точки.
Геометрия и роль КТ
Совокупность расстояний между определенными точками кузова отечественных автомобилей и иномарок называется геометрией. Дистанции между кузовными точками Приоры, Ваз 2106, 2107, 21099, 2110, Пежо 605, БМВ е34 и другими автомоделями предусматривают точное положение всех элементов автомобильного остова. Даже малый сдвиг тех или иных размеров уже скажется на работе определенных узлов и механизмов, фиксирующихся непосредственно к самому остову.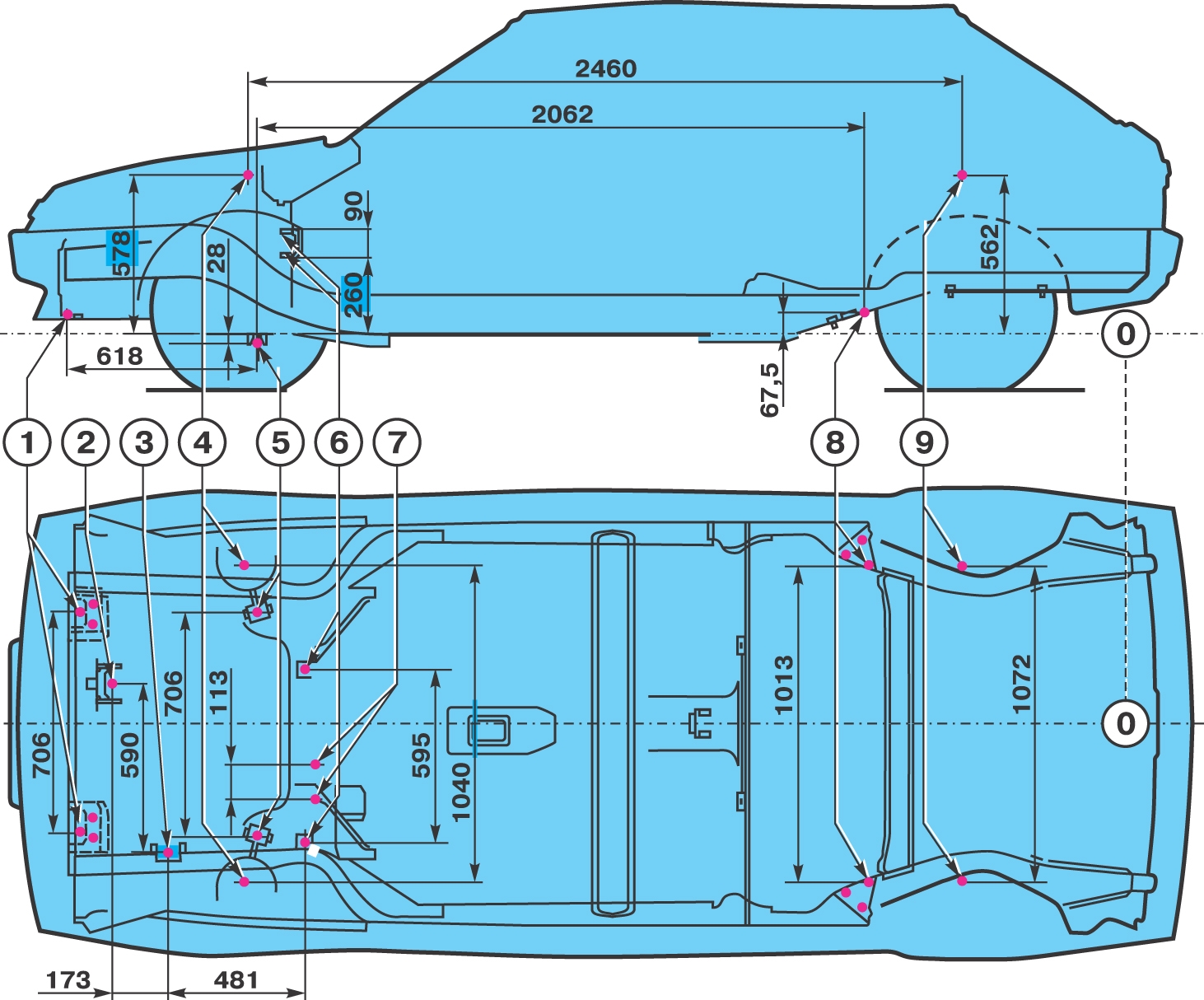
Примечание. Известными для многих специалистов контрольными точками или КТ являются размеры дверных проемов, дистанции между КТ моторного отсека и багажника. Эксперт по этим самым точкам как бы читает состояние кузова, определяет, нарушена ли геометрия и насколько.
Шаги между КТ кузова Пежо 605
Шаги между лонжеронами, амортизационными чашками и другими составляющими автоостова Приоры, Ланоса, Калины, вазовских моделей 2106, 2107, 21099 и 2110 считаются наиболее важными, так как кузов в этих зонах выполняет несущую роль для элементов ходовой системы.
Нарушения геометрии
Разные автомобили могут иметь совершенно разные значения между КТ. Отечественная модели, такие как Приора, Нива, 2106, 2107, 21099 и 2110, как правило, имеют свои значения. Производители иномарок Пежо, Опель, Нексия, Ланос могут устанавливать иные значения.
Геометрия кузова может нарушаться по ряду причин. Как правило, большинство проблем возникает в процессе активной эксплуатации машины на дорогах с неровным покрытием, регулярным преодолением препятствий и из-за аварий.
Ваз 21099 контрольные размеры
В зависимости от причины, повлиявшей на изменение конструкции, трансформируются и стандартные значения между КТ. Другими словами, если такая машина как Пежо 605 или Ланос случайно наезжает на твердое препятствие, основной удар принимает на себя подвеска. Но остальные элементы кузова тоже деформируются, принимая на себя воздействие физической силы. Это происходит в большинстве случаев постепенно и незаметно для владельца.
Стимул для осуществления квалифицированной проверки появляется, как правило, большей частью перед покупкой б/у машины. Покупатель, опасаясь быть обманутым, старается досконально проверить все недостатки автомашины. Определение дистанций между КТ помогает ему выяснить, была ли покупаемая им Приора в аварии или нет.
Да и вообще, проверка позволит узнать, как эксплуатировалась та же Приора в течении всего времени. В редких случаях размеры между КТ диагностируются в целях определения качества ремонта, проведенного на кузове.
Ну и зря, ведь во многих случаях машина, которая с виду смотрится превосходно, имеет деформированный кузов. Благодаря современным передовым технологиям и приемам удается «выгладить» кузов, сделать его привлекательным, без устранения деформаций. К сожалению, многие недобросовестные продавцы идут на этот шаг.
Ланос и КТ кузова
Примечательно, что самые ответственные автовладельцы, имеющие определенный опыт, проводят замеры между КТ регулярно. И это очень верно, так как данный процесс входит в обязательную процедуру по уходу за кузовом.
Даже после восстановительных работ владельцы автомобилей Приора или Пежо 605, а также многих других моделей не уделяют никакого внимания замерам, доверяя полностью специалистам из СТО. Затем, когда возникают уже нешуточные проблемы, они удивляются, почему же все так произошло.
Характерные симптомы деформации автомобильного остова
Для автовладельцев, которые считают регулярные замеры расстояний между КТ непозволительной тратой времени и средств, существует определенный список признаков. Их сопоставление даст понять, насколько кузов нуждается в «лечении». Чем раньше будут выявлены признаки, тем меньше денег придется выложить владельцу на сложный ремонт.
Их сопоставление даст понять, насколько кузов нуждается в «лечении». Чем раньше будут выявлены признаки, тем меньше денег придется выложить владельцу на сложный ремонт.
Итак, наиглавнейшим признаком деформации принято считать плохо запирающиеся/отпирающиеся двери той же Приоры или Пежо 605. Если только это не причина проседания дверей, то деформация автомобильного остова в зонах стоек и других элементов бесспорна.
Геометрия кузовов автомобилей БМВ
Другим, не менее распространенным и более опасным признаком считается потеря нормального управления транспортным средством на скорости выше 50 км/ч. В этих случаях автомобиль тянет в стороны, бросает, кузов вибрирует, и продолжать движение в таком случае крайне опасно для жизни.
Помните, что регулярно проводить замеры между КТ – это обязанность автомобилиста, который считает уход за автомобилем и его кузовом важным делом. Более конкретная информация о проведении замеров и восстановлении геометрии кузова приведена в других публикациях сайта.
Элементы управления на панели геометрии в Motion
Панель «Геометрия» в Инспекторе форм содержит элементы управления для изменения типа фигуры, закрытия или открытия фигуры, а также для индивидуальной настройки положения контрольных точек фигуры.
Элементы управления панели «Геометрия» доступны для всех форм, независимо от того, что выбрано во всплывающем меню «Тип кисти» на панели «Стиль». Вы можете изменить тип фигуры в любой момент. Изменение типа фигуры меняет ее форму. Например, один набор контрольных точек создает следующие три формы, в зависимости от выбранного типа формы:
Панель геометрии содержит следующие настраиваемые элементы управления:
Элементы управления базовой геометрией
Округлость: Ползунок (доступен когда выбрана простая форма прямоугольника, форма Безье или форма B-сплайна), который регулирует округлость углов формы.Используйте этот элемент управления для создания прямоугольников со скругленными углами или для сглаживания краев любой формы.

Кривизна: Ползунок (доступен при выборе простой формы круга), который регулирует степень кривизны круга. Если установлено значение 100%, форма будет эллиптической. Если установлено значение 0%, форма прямоугольная.
Сохранить масштаб: Флажок (доступен, когда выбрана простая форма прямоугольника, форма Безье или форма B-сплайна), который определяет, является ли параметр «Округлость» абсолютным или относительным к общему размеру формы.Когда этот флажок установлен, округлость остается примерно на том же процентном соотношении кривизны, что и масштабируемый объект. Когда этот флажок не установлен, кривизна изменяется по мере изменения общей формы.
Радиус: Ползунок (доступен, когда выбрана простая круглая форма), который управляет шириной и высотой формы. Щелкните треугольник раскрытия, чтобы открыть отдельные ползунки X (ширина) и Y (высота).
Размер: Ползунок (доступен, когда выбрана простая прямоугольная форма), который управляет масштабом формы.
 Щелкните треугольник раскрытия, чтобы открыть отдельные ползунки ширины и высоты.
Щелкните треугольник раскрытия, чтобы открыть отдельные ползунки ширины и высоты.Тип формы: Всплывающее меню (доступно, когда выбрана сложная фигура с контрольными точками), в котором задается тип контрольных точек, используемых для определения формы. Например, если вы изначально создали форму Безье, вы можете выбрать в этом меню B-сплайн, чтобы превратить каждую контрольную точку Безье в контрольную точку B-сплайна. Изменение типа формы не приводит к перемещению контрольных точек, хотя форма меняется, иногда значительно.Есть три варианта:
Линейный: Все контрольные точки соединены твердыми углами, и полученная форма представляет собой многоугольник. Контрольные точки линейной формы лежат прямо на ее краях.
Безье: Контрольные точки могут представлять собой сочетание кривых Безье и твердых углов, создавая любую форму. Контрольные точки формы Безье лежат прямо на ее краю.
B-сплайн: Контрольные точки — это все точки B-сплайна с разной степенью кривизны.
 Контрольные точки B-сплайна лежат внутри, снаружи или на краю фигуры и соединены рамкой B-сплайна.
Контрольные точки B-сплайна лежат внутри, снаружи или на краю фигуры и соединены рамкой B-сплайна.
Закрыто: Флажок (доступен, когда выбрана сложная фигура с контрольными точками), при выборе которого соединяются первая и последняя точки открытой фигуры. Если вы выберете замкнутую фигуру на холсте, этот флажок будет установлен. Снятие этого флажка отключает первую и последнюю точки, превращая объект в открытую форму.
Преобразовать в точки: Кнопка (доступна, если выбрана простая фигура), при нажатии на которую простая форма преобразуется в сложную форму с редактируемыми контрольными точками. См. Раздел Преобразование формы или маски в контрольные точки в движении.
Элементы управления контрольными точками
Когда выбрана сложная форма с контрольными точками, этот список становится доступным, отображая параметры положения X и Y для контрольных точек формы. Список контрольных точек также содержит одно меню анимации (стрелка вниз, которая появляется при наведении указателя на правую часть строки заголовка контрольных точек), которое влияет на все контрольные точки, позволяя добавлять ключевые кадры, сбрасывать анимацию фигуры, отображать кривая анимации в редакторе ключевых кадров и т. д.Дополнительные сведения об использовании меню «Анимация» см. В разделе «Элементы управления меню анимации в движении».
д.Дополнительные сведения об использовании меню «Анимация» см. В разделе «Элементы управления меню анимации в движении».
Что означает NURBS и почему меня это должно волновать? [McNeel Wiki]
Что такое NURBS ?
Слово NURBS является аббревиатурой от неоднородного рационального B-сплайна. Неравномерные рациональные B-шлицы могут представлять трехмерную геометрию.
Геометрия NURBS обладает пятью важными качествами, которые делают ее идеальным выбором для компьютерного моделирования.
Существует несколько стандартных способов обмена геометрией NURBS.Это означает, что клиенты могут и должны рассчитывать на возможность перемещать свои ценные геометрические модели между различными программами моделирования, визуализации, анимации и инженерного анализа. Они могут хранить геометрическую информацию таким образом, чтобы ее можно было использовать через 20 лет.
NURBS имеет точное и хорошо известное определение.
 Большинство крупных университетов преподают математику и информатику геометрии NURBS. Это означает, что поставщики специализированного программного обеспечения, группы инженеров, фирмы промышленного дизайна и анимационные компании, которым необходимо создавать собственные программные приложения, могут найти обученных программистов, способных работать с геометрией NURBS.
Большинство крупных университетов преподают математику и информатику геометрии NURBS. Это означает, что поставщики специализированного программного обеспечения, группы инженеров, фирмы промышленного дизайна и анимационные компании, которым необходимо создавать собственные программные приложения, могут найти обученных программистов, способных работать с геометрией NURBS.NURBS точно отображает как стандартные геометрические объекты, такие как линии, круги, эллипсы, сферы и торы, так и произвольную геометрию, например тела автомобилей и человеческие тела.
Количество информации, требуемой для NURBS-представления части геометрии, намного меньше, чем количество информации, требуемой для обычных фасетных аппроксимаций.
Правило оценки NURBS, обсуждаемое ниже, может быть эффективно и точно реализовано на компьютере.
Есть много способов ответить на этот вопрос. Если вам комфортно читать математические формулы, вы можете получить более подробную информацию в Книгах и статьях в разделе NURBS на веб-сайте openNURBS .
Rhino использует NURBS для представления кривых и поверхностей. Кривые и поверхности NURBS ведут себя аналогичным образом и имеют много терминологии. Поскольку кривые описать проще всего, мы рассмотрим их подробно. В Rhino есть инструменты для обработки поверхностей, аналогичные инструментам кривых, упомянутым ниже.
Кривая NURBS определяется четырьмя вещами: 90–117 градусами, контрольными точками, узлами и правилом оценки .
градусов — целое положительное число.
Обычно это число 1, 2, 3 или 5. Линии и полилинии Rhino имеют степень 1. Круги Rhino имеют степень 2. И большинство кривых произвольной формы Rhino имеют степень 3 или 5. Rhino позволит вам работать с NURBS, которые имеют степень от От 1 до 32. Иногда используются термины линейный, квадратичный, кубический и пятый.Линейный означает степень 1, квадратичный означает степень 2, кубический означает степень 3, а квинтичный означает степень 5.
Вы можете увидеть ссылки на порядок кривой NURBS. Порядок кривой NURBS — положительное целое число, равное (степень + 1). Следовательно, степень равна порядку-1.
Порядок кривой NURBS — положительное целое число, равное (степень + 1). Следовательно, степень равна порядку-1.
Можно увеличивать степень кривой NURBS и не изменять ее форму. Невозможно уменьшить градус кривой NURBS без изменения ее формы. Rhino предоставляет инструменты, которые могут изменять градусы на любое значение в диапазоне от 1 до 32.
Контрольные точки представляют собой список не менее (градус + 1) точек.
Один из самых простых способов изменить геометрию кривой NURBS — переместить ее контрольные точки. Rhino предоставляет несколько способов перемещения контрольных точек. Чтобы выполнить большие корректировки произвольной формы, просто перетащите контрольную точку с помощью мыши. Rhino предоставляет другие инструменты, предназначенные для небольших точных настроек.
Контрольные точки имеют связанный номер, называемый весом .За некоторыми исключениями, веса — положительные числа. Когда все контрольные точки кривой имеют одинаковый вес (обычно 1), кривая нерациональна. В противном случае кривая называется рациональной. R в NURBS обозначает рациональное и указывает на то, что NURBS-кривая может быть рациональной. На практике большинство кривых NURBS нерациональны. Несколько кривых NURBS, окружности и эллипсы, являющиеся яркими примерами, всегда рациональны. Rhino предоставляет инструменты для проверки и изменения веса контрольных точек.
В противном случае кривая называется рациональной. R в NURBS обозначает рациональное и указывает на то, что NURBS-кривая может быть рациональной. На практике большинство кривых NURBS нерациональны. Несколько кривых NURBS, окружности и эллипсы, являющиеся яркими примерами, всегда рациональны. Rhino предоставляет инструменты для проверки и изменения веса контрольных точек.
Узлы — это список чисел в градусах + N-1, где N — количество контрольных точек. Иногда этот список чисел называют вектором узла. В этом термине слово «вектор» не означает трехмерное направление.
Этот перечень номеров узлов должен удовлетворять нескольким техническим условиям. Стандартный способ удовлетворить технические условия — требовать, чтобы числа оставались неизменными или увеличивались по мере продвижения по списку, и ограничивать количество повторяющихся значений не более, чем на степень.Например, для кривой NURBS степени 3 с 11 контрольными точками:
Список номеров 0,0,0,1,2,2,2,3,7,7,9,9,9 является удовлетворительным списком узлов.

Список 0,0,0,1,2,2,2,2,7,7,9,9,9 неприемлем, потому что там четыре двойки, а четыре больше степени.
Количество повторений значения узла равно кратности узла . В предыдущем примере удовлетворительного списка узлов значение узла 0 имеет кратность три, значение узла 1 имеет кратность один, значение узла 2 имеет кратность три, значение узла 7 имеет кратность два, а значение узла 9 имеет кратность три.Значение узла — это узел полной кратности, если он повторяется много раз. В этом примере значения узлов 0, 2 и 9 имеют полную кратность. Значение узла, которое появляется только один раз, является простым узлом. В этом примере значения узлов 1 и 3 являются простыми узлами.
Если список узлов начинается с узла полной кратности, за ним следуют простые узлы, заканчиваются узлом полной кратности и значения расположены на равном расстоянии, то узлы являются однородными. Например, если кривая NURBS степени 3 с 7 контрольными точками имеет узлы 0,0,0,1,2,3,4,4,4, то кривая имеет равномерные узлы. Узлы 0,0,0,1,2,5,6,6,6 неоднородны. Неоднородные сучки называются неоднородными. NU в NURBS означает неоднородность и указывает на то, что узлам на кривой NURBS разрешено быть неоднородными.
Узлы 0,0,0,1,2,5,6,6,6 неоднородны. Неоднородные сучки называются неоднородными. NU в NURBS означает неоднородность и указывает на то, что узлам на кривой NURBS разрешено быть неоднородными.
Повторяющиеся значения узлов в середине списка узлов делают кривую NURBS менее гладкой. В крайнем случае, узел полной множественности в середине списка узлов означает, что на кривой NURBS есть место, которое можно согнуть в резкий перегиб. По этой причине некоторые дизайнеры любят добавлять и удалять узлы, а затем корректировать контрольные точки, чтобы сделать кривые более плавными или изогнутыми.В Rhino есть инструменты для удаления и добавления узлов. Поскольку количество узлов равно (N + степень 1), где N — количество контрольных точек, добавление узлов также добавляет контрольные точки, а удаление узлов удаляет контрольные точки. Узлы можно добавлять без изменения формы кривой NURBS. В общем, удаление узлов изменит форму кривой. Rhino предоставляет расширенный интерфейс удаления узлов, который автоматически выполняет соответствующее удаление узлов при удалении контрольной точки.
Распространенное заблуждение состоит в том, что каждый узел связан с контрольной точкой.Это верно только для NURBS степени 1 (полилиний). Для NURBS более высокой степени существуют группы узлов 2 x степени, которые соответствуют группам контрольных точек степени + 1. Например, предположим, что у нас есть NURBS степени 3 с 7 контрольными точками и узлами 0,0,0,1,2,5,8,8,8.
Первые четыре контрольные точки сгруппированы с первыми шестью узлами.
Контрольные точки со второй по пятую сгруппированы узлами 0,0,1,2,5,8.
Контрольные точки с третьей по шестую сгруппированы с узлами 0,1,2,5,8,8.
Последние четыре контрольные точки сгруппированы по последним шести узлам.
Некоторым разработчикам моделей, использующим старые алгоритмы для оценки NURBS, требуется два дополнительных значения узлов, чтобы в сумме составило градус + N + 1 узел. Когда Rhino при необходимости экспортирует и импортирует геометрию NURBS, он автоматически добавляет и удаляет эти два лишних узла.
Правило оценки использует математическую формулу, которая принимает число и присваивает балл.
Формула включает градус, контрольные точки и узлы.В формуле есть некоторые вещи, называемые базисными функциями B-сплайна. BS в NURBS означает B-сплайн. Номер, с которого начинается правило оценки, называется параметром. Вы можете думать о правиле оценки как о черном ящике, который съедает параметр и дает точку. Степень, узлы и контрольные точки определяют, как работает черный ящик.
У Rhino есть инструменты оценки. Вы можете выбрать кривую NURBS, ввести значение параметра и создать соответствующую точку.
Концептуально узлы определяют базисные функции B-сплайна.Значения базовых функций B-сплайна в параметре определяют, как контрольные точки и веса усредняются вместе для получения точки. Подробное обсуждение правила оценки и базовых функций B-сплайна доступно во многих учебниках и на веб-страницах.
Точка | Линия | Радиально от точки | Угол: Ориентация линии от маркера. Длина: Расстояние линии от конца до конца. Значение по умолчанию — 5 пунктов. Регулировка этого значения изменяет длину динамической линии. |
Многоугольник | Буфер | Размер: Расстояние от края маркера. Значение по умолчанию — 1 пункт. При указании значений больше 1 вокруг маркера создается динамический многоугольник большего размера. | |
Правильный многоугольник | Радиус: Расстояние от центра многоугольника. Значение по умолчанию — 2,5 пункта. При указании значений больше 1 вокруг маркера создается динамический многоугольник большего размера. Ребра: Количество сторон многоугольника. Угол: Величина поворота многоугольника.Значение по умолчанию — 0 (ноль) градусов. | ||
Линия | Линия | Добавить контрольные точки | Угловой допуск: Максимальная величина отклонения от одного сегмента к другому в вершине. Значение по умолчанию — 120 градусов. Значения угла от 180 до 360 интерпретируются так же, как значения от 0 до 180. Значения угла от 180 до 360 такие же, как 0 (ноль). |
Стрелка | Стиль: Указывает тип отображаемой стрелки.Возможные варианты: Open Ended, Block и Crossed. Ширина: Указывает расстояние между линиями, образующими основную часть стрелки. Значение по умолчанию — 20 пунктов. | ||
Cut | Начало резки: Указывает расстояние от начала строки, на котором начинается отображение хода.Начало строки определяется направлением оцифровки строки. Расстояние наносится по линии. Значение по умолчанию — 1 пункт. Обрез конца: Указывает расстояние от конца строки, с которого начинается отображение хода. Окончание строки определяется направлением оцифровки строки. Расстояние наносится по линии. Значение по умолчанию — 1 пункт. Инвертировать: Указывает, что эффект должен применяться противоположным образом. | ||
Штрихи | Шаблон: Указывает расстояние для каждого штриха и пробела. Может быть несколько значений тире и пробела, чтобы сформировать сложный узор. Штрих — это символическая часть штриха, а пробел — несимволизированная часть штриха. Когда длина линии не поддерживает отображение всего рисунка, рисунок сжимается, чтобы соответствовать.Использование нечетного числа значений приводит к удвоению общей длины шаблона. Вторая половина узора — обратная первой половине. Допустимо использование значения 0 (ноль). Эти параметры позволяют создавать более сложные образцы тире. Значения по умолчанию — 10 пунктов и 10 пунктов. Окончания: Положение штриха вдоль линии. Возможные варианты: Без ограничений, С половинным шаблоном, С полным шаблоном, С половинным промежутком, С полным промежутком и Пользовательский. Позиция: Указывает, где должен начинаться массив относительно начальной точки геометрии. Он сдвигает весь узор вдоль линии на указанное расстояние. Отрицательные числа указывают на сдвиг влево, положительные числа — на сдвиг вправо. Это свойство действует только в том случае, если для параметра Endings установлено значение No constraint или Custom.При построении правила представления это свойство динамически выводится из значения Step и динамически обновляется во время построения или модификации правила, когда обновляется свойство Endings. Смещение в конце: Указывает, где должен заканчиваться массив относительно конечной точки геометрии. Отрицательные числа указывают на сдвиг влево, положительные числа — на сдвиг вправо. | ||
Расширение | Источник: Источник расширения, добавляемого к строке. Отклонение: Угол отклонения, используемый для удлинения. Укажите 0 для отсутствия прогиба. Длина: Длина расширения, которое создается динамически. | ||
Изгиб | Длина: Длина сегмента, образующего излом на линии. Позиция: Положение центра излома в процентах от начала входной геометрии. Угол: Угол изгиба линии, измеренный в градусах. | ||
Перемещение | Смещение по оси X: Расстояние для перемещения символа по оси x от геометрии элемента. Значение по умолчанию — 1 пункт. Смещение по оси Y: Расстояние для перемещения символа по оси Y от геометрии элемента.Значение по умолчанию -1 pt. | ||
Смещение | Смещение: Расстояние штриха, перпендикулярного геометрии линии. Значение по умолчанию — 1 пункт. Метод: Указывает способ отображения штрихов в углах. Доступны варианты со скошенной кромкой, скошенной кромкой, скругленной и квадратной. Скошенный соответствует точной форме вокруг угла линии. Bevelled следует по кратчайшему прямому пути через угол линии. Скругленный следует по пути на равном расстоянии от угла линии.Квадрат следует по прямому пути через угол линии. Опция: Указывает способ обработки штрихов сложной геометрией. Возможны варианты «Быстро» и «Точно». Fast игнорирует сложную геометрию и применяет наилучшее соответствие к символу штриха. Accurate соответствует сложной геометрии и обеспечивает точное соответствие символу штриха. Значение по умолчанию — Быстро. Счетчик: Количество смещений хода. Значение по умолчанию — 1. | ||
Смещение тангенса | Метод: Начало смещения касательной для линии. Смещение: Расстояние, на которое геометрия перемещается по касательной. | ||
Реверс | Реверс: Указывает, нужно ли перевернуть динамический вывод предыдущего геометрического эффекта. Выбрано значение по умолчанию. | ||
Повернуть | Угол: Указывает величину поворота для символа штриха.Значение по умолчанию — 15 градусов. | ||
Масштаб | X-коэффициент: Указывает величину изменения размера символа штриха по оси x. Значение выражается в соотношении / процентном соотношении. Значение по умолчанию — 1,15 или 115 процентов. Коэффициент Y: Указывает величину изменения размера символа штриха по оси Y. Значение выражается в соотношении / процентном соотношении. Значение по умолчанию — 1,15 или 115 процентов. | ||
Упростить | Допуск: Указывает расстояние вдоль контура многоугольника для удаления вершин из символа штриха. | ||
Гладкий | Плоский допуск: Указывает расстояние вдоль линии, на котором должны быть сегменты динамической кривой Безье.Значение по умолчанию — 1 пункт. Значение больше 1 учитывает меньшее количество сегментов для динамической кривой Безье контура многоугольника. | ||
Подавить | Подавить: Указывает, следует ли подавлять участки линейных объектов между двумя наборами контрольных точек. Подавление инверсии: Установленный флажок означает, что строка начинается с подавленного (не видимого) участка. Если флажок не установлен, строка начинается с неподавленного (видимого) раздела. | ||
Волна | Период: Указывает расстояние вдоль линии для отображения кривой для символа штриха. Значение по умолчанию — 3 пункта. Ширина: Указывает расстояние, перпендикулярное линии для отображения кривой для символа штриха. Значение по умолчанию — 2 пункта. Стиль: Указывает форму отображаемой кривой. Возможные варианты: Sinus, Square, Triangle и Random. Sinus отображает синусоидальную кривую или форму полумесяца.Квадрат отображает трехстороннюю кривую прямоугольной формы. Треугольник отображает двустороннюю кривую треугольной формы. В случайном порядке отображается синусоидальная кривая со случайным изменением периода и ширины кривой. Значение по умолчанию — Sinus. Seed: Указывает начальное значение для генерации случайного числа. Это случайное число используется типом Style Random для определения размера маркера. Значение по умолчанию — 1. | ||
Многоугольник | Буфер | Размер: Расстояние от края штриха.Значение по умолчанию — 1 пункт. | |
Ограждающий многоугольник | Метод: Указывает способ создания геометрии многоугольника вокруг обводки. Доступны следующие варианты: «Закрытый путь», «Выпуклая оболочка» и «Прямоугольник». Close path создает многоугольник, соединяющий оба конца линии друг с другом. Выпуклая оболочка создает многоугольник, который приближается к форме линии. Прямоугольник формирует многоугольник, равный пространственной огибающей линии.Значение по умолчанию — прямоугольник. | ||
Конический многоугольник | From width: Указывает ширину в начале линии, которая будет использоваться для создания многоугольника. Значение по умолчанию — 0 pt (ноль). По ширине: Указывает ширину в конце линии, которая будет использоваться для создания многоугольника. Значение по умолчанию — 1 пункт. Длина: Указывает расстояние вдоль линии, которое будет использоваться для создания многоугольника.Значение по умолчанию — 0 pt (ноль). | ||
Многоугольник | Линия | Cut | Begin cut: Указывает расстояние от конечной точки многоугольника, на котором начинается отображение штриха. Расстояние применяется по контуру многоугольника. Значение по умолчанию — 1 пункт. Концевой вырез: Указывает расстояние от конечной точки многоугольника, на котором начинается отображение обводки.Расстояние применяется по контуру многоугольника. Значение по умолчанию — 1 пункт. Инвертировать: Указывает, что эффект должен применяться противоположным образом. При этом символ обводки отображается только в конечной точке многоугольника, а остальная часть контура многоугольника не имеет символов. Значение по умолчанию не отмечено. |
Штрихи | Шаблон: Указывает расстояние для каждого штриха и пробела. Может быть несколько значений тире и пробела, чтобы сформировать сложный узор.Штрих — это символическая часть штриха, а пробел — несимволизированная часть штриха. Когда длина линии не поддерживает отображение всего рисунка, рисунок сжимается, чтобы соответствовать. Использование нечетного числа значений приводит к удвоению общей длины шаблона. Вторая половина узора — обратная первой половине. Допустимо использование значения 0 (ноль). Эти параметры позволяют создавать более сложные образцы тире. Значения по умолчанию — 10 пунктов и 10 пунктов. Окончаний: Положение штриха вдоль контура многоугольника. Возможные варианты: Без ограничений, С половинным шаблоном, С полным шаблоном, С половинным промежутком, С полным промежутком и Пользовательский. Пользовательский подгоняет узор по длине элемента, немного изменяя зазоры. Никакое ограничение не регулирует зазоры вообще, а это означает, что шаблон вряд ли точно соответствует длине элемента. По умолчанию используется половинный узор. Позиция: Указывает, где должен начинаться массив относительно начальной точки геометрии.Он сдвигает весь узор вдоль линии на указанное расстояние. Отрицательные числа указывают на сдвиг влево, положительные числа — на сдвиг вправо. Это свойство действует только в том случае, если для параметра Endings установлено значение No constraint или Custom. При построении правила представления это свойство динамически выводится из значения Step и динамически обновляется во время построения или модификации правила, когда обновляется свойство Endings. Смещение в конце: Указывает, где должен заканчиваться массив относительно конечной точки геометрии.Отрицательные числа указывают на сдвиг влево, положительные числа — на сдвиг вправо. Это свойство действует, только если для параметра Endings установлено значение Custom. При построении правила представления этот параметр динамически извлекается из значения Step и динамически обновляется во время построения или модификации правила, когда обновляется свойство Endings. | ||
Многоугольник | Добавить контрольные точки | Угловой допуск: Максимальная величина отклонения от одного сегмента к другому в вершине.Значение по умолчанию — 120 градусов. Значения угла от 180 до 360 интерпретируются так же, как значения от 0 до 180. Значения угла от 180 до 360 такие же, как 0 (ноль). | |
Буфер | Размер: Расстояние от края контура многоугольника. Значение по умолчанию — 1 пункт. | ||
Пончик | Ширина: Указывает расстояние от края многоугольника, на котором должен отображаться символ заливки.Значение по умолчанию — 2 пункта. Метод: Указывает способ отображения штрихов в выпуклых углах многоугольника. Возможные варианты: Mitered, Bevelled, Rounded и True buffer. Скошенный соответствует точной форме вокруг выпуклого угла многоугольника. Скос следует по кратчайшему прямому пути через выпуклый угол многоугольника. Скругленный следует по пути равного расстояния вокруг выпуклого угла многоугольника. True buffer использует алгоритм буфера для обхода выпуклых углов.Значение по умолчанию — Mitered. Простой: Указывает, динамически ли упрощаются сложные геометрические фигуры для создания бублика. По умолчанию это отмечено. | ||
Ограждающий полигон | Метод: Указывает способ создания полигональной геометрии вокруг полигонального объекта. Доступны следующие варианты: «Закрытый путь», «Выпуклая оболочка» и «Прямоугольник». Замыкший путь генерирует полигон, который соответствует геометрии полигонального объекта.Выпуклая оболочка создает полигон с минимальным количеством сторон, окружающих полигональный объект. Прямоугольник формирует полигон, равный пространственной оболочке полигонального объекта. Значение по умолчанию — прямоугольник. | ||
Перемещение | Смещение по оси X: Расстояние для перемещения символа по оси x от геометрии элемента. Значение по умолчанию — 1 пункт. Смещение по оси Y: Расстояние для перемещения символа по оси Y от геометрии элемента.Значение по умолчанию -1 pt. | ||
Смещение | Смещение: Расстояние контура многоугольника перпендикулярно его геометрии. Значение по умолчанию — 1 пункт. Метод: Указывает способ отображения заливки в углах. Доступны варианты со скошенной кромкой, скошенной кромкой, скругленной и квадратной. Скошенный соответствует точной форме вокруг угла многоугольника. Скос следует по кратчайшему прямому пути через угол многоугольника.Скругленный следует за углом многоугольника на равном расстоянии. Квадрат следует по прямому пути через угол многоугольника. Значение по умолчанию — Квадрат. Опция: Указывает способ обработки контура многоугольника сложной геометрии. Возможны варианты «Быстро» и «Точно». Fast игнорирует сложную геометрию и применяет наилучшее соответствие к контуру многоугольника. Точность учитывает сложную геометрию и обеспечивает точное соответствие контуру многоугольника. Значение по умолчанию — Быстро. Счетчик: Количество смещений хода.Значение по умолчанию — 1. | ||
Повернуть | Угол: Указывает величину поворота для символа заливки. Значение по умолчанию — 15 градусов. | ||
Масштаб | X-коэффициент: Указывает величину изменения размера символа заливки по оси x. Значение выражается в соотношении / процентном соотношении. Значение по умолчанию — 1,15 или 115 процентов. Коэффициент Y: Указывает величину изменения размера символа заливки по оси Y.Значение выражается в соотношении / процентном соотношении. Значение по умолчанию — 1,15 или 115 процентов. | ||
Упростить | Допуск: Указывает расстояние вдоль контура многоугольника для удаления вершин из символа штриха. Значение по умолчанию — 10 пунктов. Значение менее 10 поддерживает большую часть исходной формы контура многоугольника. Значение больше 10 сохраняет меньшую исходную форму контура многоугольника. | ||
Гладкий | Плоский допуск: Указывает расстояние вдоль контура многоугольника для рассмотрения сегментов для динамической кривой Безье контура многоугольника.Значение по умолчанию — 1 пункт. Значение больше 1 учитывает меньшее количество сегментов для динамической кривой Безье контура многоугольника. | ||
Волна | Период: Указывает расстояние вдоль контура многоугольника для отображения кривых для символа заливки. Значение по умолчанию — 3 пункта. Ширина: Указывает расстояние, перпендикулярное контуру многоугольника, для отображения кривых для символа заливки. Значение по умолчанию — 2 пункта. Стиль: Указывает форму кривых, отображаемых вдоль контура многоугольника. Возможные варианты: Sinus, Square, Triangle и Random. Sinus отображает синусоидальную кривую или форму полумесяца. Квадрат отображает трехстороннюю прямоугольную форму. Треугольник отображает двустороннюю треугольную форму. В случайном порядке отображается синусоида со случайным изменением периода и ширины контура, а внутренняя часть многоугольника остается полностью символизированной. Значение по умолчанию — Sinus. Seed: Указывает начальное значение для генерации случайного числа.Это случайное число используется типом Style Random для определения размера маркера. Значение по умолчанию — 1. |
Моделирование форм каналов и связанных осадочных объектов с использованием граничного представления на основе неоднородных рациональных B-сплайнов
Abrahamsen P, Fjellvoll B, Hauge R (2007) Стохастическое моделирование на основе процессов глубоководные морские водоемы. В: EAGE petroleum geostatistics
Abreu V, Sullivan M, Pirmez C, Mohrig D (2003) Пакеты боковых аккреций (накладки): важный элемент коллектора в глубоких извилистых каналах.Mar Pet Geol 20 (6): 631–648
Статья Google Scholar
Аллен Дж. Р. (1963) Классификация перекрестно-стратифицированных единиц. С примечаниями об их происхождении. Седиментология 2 (2): 93–114
Статья Google Scholar
Альпак Ф.О., Бартон М.Д., Нарук С.Дж. (2013) Влияние мелкомасштабной архитектуры турбидитовых каналов на характеристики глубоководных коллекторов. AAPG Bull 97 (2): 251–284.DOI: 10.1306 / 04021211067
Артикул Google Scholar
Арнотт Р. (2010) Глубоководные отложения и осадочные системы. В: Джеймс Н., Далримпл Р. (ред.) Фациальная модель 4. Сент-Джонс: Геологическая ассоциация Канады, стр. 295–322
Бертончелло А., Каерс Дж. К., Бивер П., Камон Г. (2008) Геостатистика на стратиграфических сетках. В: Ortiz J, Emery X (eds) Proc. восьмой конгресс по геостатистической геостатистике, т. 2.Gecamin ltd, pp 677–686
Bertoncello A, Sun T., Li H, Mariethoz G, Caers J (2013) Согласование геологических моделей на поверхности с данными о скважинах и толщинах. Math Geosci 45 (7): 873–893
Статья Google Scholar
Бхаттачарья Дж. (2010) Дельты. In: James N, Dalrymple R (eds) Facies model 4. St. John’s: Geological Association of Canada, pp. 233–264
Boisvert JB, Pyrcz MJ, Deutsch CV (2007) Многоточечная статистика для выбора обучающего изображения .Nat Resour Res 16 (4): 313–321
Статья Google Scholar
Comunian A, Jha SK, Giambastiani BM, Mariethoz G, Kelly BF (2014) Обучающие изображения из методов имитации процесса. Math Geosci 46 (2): 241–260
Статья Google Scholar
Десбарац А. (1987) Численная оценка эффективной проницаемости в песчано-сланцевых пластах. Water Resour Res 23 (2): 273–286
Статья Google Scholar
Deutsch CV, Wang L (1996) Иерархическое объектно-стохастическое моделирование речных резервуаров.Math Geol 28 (7): 857–880
Статья Google Scholar
Deutsch C, Tran T (2002) Fluvsim: программа для объектно-стохастического моделирования речных осадочных систем. Comput Geosci 28 (4): 525–535
Статья Google Scholar
Deutsch C, Tran T (2004) Моделирование геометрии глубоководных лепестков с помощью объектно-ориентированного моделирования: Lobesim. Tech. респ., техн.представитель Университета Альберты. http://www.uofaweb.ualberta.ca/ccg//pdfs/1999%2004-LobeModeling1.pdf. Доступ 7 декабря 2015 г.
Durlofsky LJ (2005) Апскейлинг и привязка мелкомасштабных геологических моделей для моделирования потока. В: 8-й международный форум по моделированию коллектора, Остров Борромеис, стр. 20–24
Фишер Т., Уэльс Р. (1992) Рациональные сплайны и многомерное геологическое моделирование. В: Pflug R, Harbaugh J (eds) Компьютерная графика в геологии, том 41, Конспект лекций по наукам о Земле, Спрингер, Берлин, стр. 17–28
Google Scholar
Gai X, Wu Xh, Branets L, Sementelli K, Robertson G (2012) Геологическое моделирование на основе концепций с использованием представления функциональной формы.\ circ \) O
Graham GH, Jackson MD, Hampson GJ (2015) Трехмерное моделирование клиноформ в мелководных морских водоемах: часть 1. Концепции и применение. AAPG Bull 99 (06): 1013–1047. DOI: 10.1306 / 011190
Артикул Google Scholar
Haldorsen H, Lake L (1984) Новый подход к управлению сланцами в полевых моделях. Старый SPE J 24 (4): 447–457
Google Scholar
Hassanpour MM, Pyrcz MJ, Deutsch CV (2013) Улучшенные геостатистические модели наклонных гетеролитических пластов для формации Мак-Мюррей, Альберта, Канада.AAPG Bull 97 (7): 1209–1224. DOI: 10.1306 / 01021312054
Артикул Google Scholar
Holden L, Hauge R, Skare Ø, Skorstad A (1998) Моделирование речных резервуаров с помощью объектных моделей. Math Geol 30 (5): 473–496
Статья Google Scholar
Ховард А. (1996) Моделирование эволюции русла и морфологии поймы. В: Процессы поймы, стр. 15–62
Ховард А., Кнутсон Т. (1984) Достаточные условия для меандрирования реки: подход моделирования.Wat Resour Res 20 (11): 1659–1667
Статья Google Scholar
Issautier B, Fillacier S, Gallo YL, Audigane P, Chiaberge C, Viseur S (2013) Моделирование емкости и производительности \ ({\ rm CO} _2 \). Энергетические процедуры 37: 5181–5190
Джексон М., Маггеридж А. (2000) Влияние разрывных сланцев на характеристики коллектора во время горизонтального заводнения. SPE J 5 (4): 446–455
Статья Google Scholar
Джексон М.Д., Хэмпсон Г.Дж., Сеч Р.П. (2009) Трехмерное моделирование аналога резервуара парасеквенции береговая поверхность-шельф: часть 2.Геологический контроль за потоком флюидов и извлечением углеводородов. AAPG Bull 93 (9): 1183–1208. DOI: 10.1306 / 051105
Артикул Google Scholar
Journel A (1996) Условное моделирование геологически усредненной проницаемости блоков. J Hydrol 183 (1): 23–35
Артикул Google Scholar
Journel A, Gundeso R, Gringarten E, Yao T (1998) Стохастическое моделирование речного коллектора: сравнительный обзор алгоритмов.J Pet Sci Eng 21 (1): 95–121
Статья Google Scholar
Knighton D (2014) Речные формы и процессы: новая перспектива, 2-е изд. Рутледж, Нью-Йорк
Google Scholar
Li H, Caers J (2011) Геологическое моделирование и сопоставление истории многомасштабных барьеров потока в канальных коллекторах: методология и применение. Pet Geosci 17 (1): 17–34. DOI: 10.1144 / 1354-079309-825
Артикул Google Scholar
Lopez S (2003) Моделирование механических резервуаров: несоответствие генетическим и стохастическим. Кандидатская диссертация, Mines Paris Tech
Manchuk JG, Deutsch CV (2012) Аспекты реализации последовательного гауссовского моделирования в нерегулярных точках. Comput Geosci 16 (3): 625–637
Статья Google Scholar
Manchuk J, Leuangthong O, Deutsch CV (2005) Прямое геостатистическое моделирование на неструктурированных сетках.В: Geostatistics Banff 2004. Springer, New York, pp 85–94
Mariethoz G, Caers J (2014) Многоточечная геостатистика: стохастическое моделирование с обучающими изображениями. Wiley-Blackwell, New York
Mariethoz G, Comunian A, Irarrazaval I, Renard P (2014) Аналоговое моделирование меандрирующих каналов. Water Resour Res 50 (2): 836–854. DOI: 10.1002 / 2013WR013730
Артикул Google Scholar
McKee ED (1957) Флюм эксперименты по получению стратификации и перекрестной стратификации.Журнал Sediment Res 27 (2): 129–134. DOI: 10.1306 / 74D70678-2B21-11D7-8648000102C1865D
Google Scholar
Miall A (1985) Архитектурный элементный анализ: новый метод фациального анализа, применяемый к речным отложениям. Earth-Sci Rev 22 (4): 261–308
Статья Google Scholar
Miall A (1996) Геология речных отложений: осадочные фации.Springer, New York
Miall A (2010) Аллювиальные отложения. В: Джеймс Н., Далримпл Р. (ред.) Фациальная модель 4. Сент-Джонс: Геологическая ассоциация Канады, стр. 105–138
Мировски П.В., Тецлафф Д.М., Дэвис Р.К., Маккормик Д.С., Уильямс Н., Сигнер С. (2009 г. ) Показатели стационарности обучающих изображений для многоточечной геостатистики. Math Geosci 41 (4): 447–474
Статья Google Scholar
Nordahl K, Ringrose PS, Wen R (2005) Петрофизическая характеристика интервала гетеролитического приливного коллектора с использованием инструмента моделирования на основе процессов.Pet Geosci 11 (1): 17–28
Статья Google Scholar
Новакович Д., Уайт С., Корбеану Р., Хаммон Иии В., Бхаттачарья Дж., МакМечан Г. (2002) Гидравлические эффекты сланцев в флювиально-дельтовых отложениях: георадар, наблюдения обнажений, геостатистика и трехмерный поток моделирование песчаника Феррон, штат Юта. Math Geol 34 (7): 857–893
Статья Google Scholar
Пигл Л., Тиллер В. (1995) Книга NURBS.Springer, Лондон
Бронировать Google Scholar
Pyrcz MJ, Catuneanu O, Deutsch CV (2005) Стохастическое поверхностное моделирование лопастей турбидита. AAPG Bull 89 (2): 177–191. DOI: 10.1306 / 09220403112
Pyrcz M, Boisvert J, Deutsch C (2009) Alluvsim: программа для стохастического моделирования на основе событий речных осадочных систем. Comput Geosci 35 (8): 1671–1685. DOI: 10.1016 / j.cageo.2008.09.012
Артикул Google Scholar
Reineck HE, Singh IB (1980) Осадочные осадочные среды. Springer, Берлин
Забронировать Google Scholar
Renard P, Mariethoz G (2014) Специальный выпуск о 20-летней многоточечной статистике: часть 1. Math Geosci 46 (2): 129–131
Article Google Scholar
Rongier G, Collon P, Renard P, Ruiu J (2015) Моделирование канала с использованием L-системы, потенциальных полей и NURBS.В: Нефтяная геостатистика 2015, EAGE. DOI: 10.3997 / 2214-4609.201413604
Ruiu J, Caumon G, Viseur S, Antoine C (2014) Моделирование форм каналов с использованием граничного представления, основанного на неоднородных рациональных b-сплайнах. В кн .: Математика планеты Земля. Springer, New York, pp. 581–584
Ruiu J, Caumon G, Viseur S (2015) Полуавтоматическая интерпретация трехмерных седиментологических структур на геологических изображениях: объектно-ориентированный подход. Интерпретация 3 (3): SX63 – SX74
Сеч Р.П., Джексон М.Д., Хэмпсон Г.Дж. (2009) Трехмерное моделирование аналога коллектора парасеквенции береговая поверхность-шельф: часть 1.Поверхностное моделирование для отражения фациальной архитектуры с высоким разрешением. AAPG Bull 93 (9): 1155–1181. DOI: 10.1306 / 051104
Артикул Google Scholar
Штука А., Самсон П., Маллет Дж. Л. (1996) Петрофизическое моделирование в рамках объектно-ориентированной модели коллектора. В: Proc. Европейская конференция по трехмерному моделированию коллектора (SPE 35480)
Viseur S (2004) Определение характеристик турбидитового коллектора: объектно-ориентированное стохастическое моделирование меандрирующих каналов.Bull Soc Geol Fr 175 (1): 11–20. DOI: 10.2113 / 175.1.11
Артикул Google Scholar
Вен Р., Мартиниус А., Нэсс А., Рингроуз П. (1998) Трехмерное моделирование мелкомасштабной неоднородности в приливных отложениях — метод стохастического моделирования, основанный на процессах. В: Материалы 4-й ежегодной конференции Международной ассоциации математической геологии (IAMG). De Frede editore, Искья, стр. 129–134
1: ГЕОМЕТРИЧЕСКИЕ ОСНОВЫ ДВИЖЕНИЯ И УПРАВЛЕНИЯ | Движение, управление и геометрия: материалы симпозиума
Бобенко, А.И., А.Г. Рейман и М.А.Семенов-Тян-Шанский, 1989, «Вершина Ковалевского 99 лет спустя: пара Лакса, обобщения и явные решения», Commun. Математика. Phys . 122 , 321-354.
Brockett, R.W., 1989, «О коррекции вибрационного движения», Датчики и исполнительные механизмы 20 , 91-96.
Брокетт Р.В., 1981, «Теория управления и сингулярная риманова геометрия». В: Новые направления в прикладной математике , П.Дж. Хилтон и Г.С. Янг (ред.), Берлин, Гейдельберг, Нью-Йорк: Springer-Verlag.
Энос М. (ред.), 1993, «Динамика и управление механическими системами: падающий кот и связанные с этим проблемы», Связь института Филдса, , том. 1, Провиденс, Род-Айленд: Американское математическое общество.
Hannay, J., 1985, «Угловая переменная голономия в адиабатическом отклонении итерабельного гамильтониана», J. Phys. А 18 , 221-230.
Каммер, Д.К. и Г.Л. Грей, 1993, «Нелинейная схема управления для моделирования стока энергии в задаче Эйлера-Пуансо», J. Astron. Sci . 41 , 53-72.
Кейн Т.Р. и М. Шур, 1969, «Динамическое объяснение феномена падающей кошки», Int. J. Solid Structures 5 , 663-670.
Койллер, Дж., 1992, «Редукция некоторых классических неголономных систем с симметрией», Arch. Крыса. Мех. Анальный . 118 , 113-148.
Кришнапрасад, П.С., 1989, «Эйлеровы задачи многих тел», Cont. Математика. АМС 97 , 187-208.
Куммер М., 1981, «О построении редуцированного фазового пространства гамильтоновой системы с симметрией», Indiana Univ. Математика. J . 30 , 281-291.
Льюис, А., Р.М. Мюррей, Дж. П. Островски и Дж. Бердик, 1997, «Неголономная механика и движение: пример снейкборда», IEEE Intern. Конф. по робототехнике и автоматизации, чтобы появиться.
Марсден, Дж.Э. и Т.С. Ратиу, 1994, «Введение в механику и симметрию» Тексты по прикладной математике , Берлин, Гейдельберг, Нью-Йорк: Springer-Verlag.
Марсден, Дж. Э., Р. Монтгомери и Т. С. Ratiu, 1990, «Редукция, симметрия и фазы в механике», Memoirs AMS 436.
Монтгомери Р., 1991a, «Оптимальное управление деформируемыми телами и его связь с калибровочной теорией». В: Геометрия гамильтоновых систем, , Т. Ратиу (ред.), Берлин, Гейдельберг, Нью-Йорк: Springer-Verlag.
Монтгомери, Р., 1991b, «Насколько твердое тело вращается? Фаза Берри из 18 -го века», Am. J. Phys . 59 , 394-398.
Монтгомери Р., 1991c, «Оптимальное управление деформируемыми телами и его связь с калибровочной теорией», В Геометрия гамильтоновых систем , Т. Ратиу (ред.), Берлин, Гейдельберг, Нью-Йорк: Springer-Verlag.
Монтгомери Р., 1990, «Изоголономные проблемы и некоторые приложения», Commun.Математика. Phys . 128 , 565-592.
Монтгомери Р., 1988, «Связность, голономия которой представляет собой классические адиабатические углы Ханнея и Берри и ее обобщение на неинтегрируемый случай», Commun. Математика. Phys . 120 , 269-294.
Мюррей Р.М. и С.С. Састри, 1993, «Планирование неголономного движения: управление с использованием синусоид», IEEE Trans. Автомат. Контроль 38 , 700-716.
Ой, Ю.Г., Н.Шринат, П.С. Кришнапрасад и Дж. Э. Марсден, 1989, «Динамика связанных плоских твердых тел, часть 2: бифуркации, периодические решения и хаос», Динамика и дифференциальные уравнения 1 , 269-298.
Геометрия— SPC Wiki
Описание
Эта программа создает поверхность, вычисляя положение космического корабля, наведение космического корабля и местоположения ориентиров. Эта процедура последовательно выполняет итерацию решений для векторов наведения камеры и ориентиров.
Необходимые файлы
LMKFILES / — каталог, содержащий полный набор ориентиров.
PICTLIST.TXT — список имен изображений, созданный make_sumfiles.
LMRKLIST.TXT — список ориентиров, содержащихся в решении.
LMRKLIST1.TXT — файл, содержащий значения по умолчанию, которые должен быть прочитан набором инструментов SPC.
MAPFILES / — каталог, содержащий полный набор кейплетов.
INIT_LITHOS.TXT — текстовый файл, устанавливающий ограничения, определения и логические параметры для SPC.
SHAPE.TXT — модель формы, хранящаяся в каталоге SHAPEFILES /.
NOMINALS / — каталог, содержащий файлы изображений .NOM.
SUMFILES / — каталог, содержащий файлы изображений .SUM (обновленное изображение решения, информация о S / C и камере; lmrks и конечности).
Файлы вывода
СУММЫ / — Ориентиры добавляются в СУММФАЙЛ изображения.Положение космического аппарата / камеры / ориентация обновляются после принятия пользователем изменений центровки.
LMKFILES / — Каталог LMKFILES / обновляется и содержит образ, с которым работает пользователь.
MAPFILES / — этот каталог также обновляется, потому что вектор ориентира в заголовке MAPFILE также обновляется
Дополнительные файлы
Предупреждение пользователя
Использование геометрии
Входными данными для геометрии являются:
список операций ввода — Используйте следующие значения:
- 1: векторы ориентиров.
- 2: наведение камеры, scobj
- 0: конец.
введите количество итераций — введите желаемое число. использовать конечности для наведения? (да / нет) — Выберите, следует ли использовать конечности при определении наведения камеры. продолжить? (да / нет) — Решите, делать ли это сначала.
Вот два аннотированных образца, которые показывают геометрию входов:
ГЕОМЕТРИЯ 120 <- сделать 1, а затем 2 30 <- повторить 30 раз y <- использовать конечности для наведения n <- прекратить, когда закончите ГЕОМЕТРИЯ 20 <- сделать только 2 10 <- сделать 10 раз n <- не использовать конечности для наведения n <- остановить по завершении
По умолчанию эти операции выполняются для всех ориентиров в LMRKLIST.TXT и все изображения в PICTLIST.TXT.
Если INIT_LITHOS.TXT содержит запись
GEOPI = 'filename1' или же GEOMAP = 'filename2'
, то используемые файлы уменьшаются. "filename1" используется вместо PICTLIST.TXT, а "filename2" используется вместо LMRKLIST.TXT.
Дополнительная ссылка
Условия оценки геометрии
Состояние космического корабля - Положение и ориентация космического корабля влияет на размер и расположение тела на изображении.Ошибки отражаются В смещениях извлеченных данных изображения из кейплетов для всех кленов на изображении.
Местоположение контрольной точки - Ошибка в местоположении контрольной точки, фиксированной на теле, отражается смещениями извлеченных данных изображения для всех изображений, содержащих клёплеты.
Вращение - Ошибка преобразования инерциальных кадров в фиксированные кадры отражается в зависящих от времени смещениях в данных извлеченных изображений для всех кленов на всех изображениях.
Дифференциальный стерео - Ошибки в высоте клена относительно центра отражаются дифференциальным смещением элементов в извлеченных данных изображения в дополнение к смещениям от самих кленов.
Рисунок 00: Примеры ошибок смещения и ориентации
Более подробное описание геометрии
- Глобальное решение для позиционирования и наведения камеры, а также для определения местоположения клена на теле.
- Итерационный процесс:
- Взвешенное решение ориентиров (контрольных точек) методом наименьших квадратов на основе:
- Положение ориентира относительно космического корабля
- Относительное местоположение ориентира к ориентиру
- Положение конечности
- Начальный стартовый объект
- Взвешенное решение по методу наименьших квадратов для определения положения и наведения камеры на основе местоположения ориентира
- Номинальное наведение камеры
- Номинальное положение камеры
- Положение конечности
- Положение ориентира относительно космического корабля
- Наблюдения до и после каждого наблюдение
- Взвешенное решение ориентиров (контрольных точек) методом наименьших квадратов на основе:
Выходные ковариации из одной итерации становятся входными ковариациями для следующей итерации, поэтому схема обновления файлов сумм и файлов lmk должна включать обновление их неопределенностей.
Типичное использование - это последовательность шагов, например 120, и 3 или более итераций. Предположим, мы создали несколько новых ориентиров. Вышеупомянутые шаги означают, что мы сначала используем априорную информацию о местоположении и указании для определения ориентиров. Затем, поскольку есть некоторая ошибка во входных данных априорного положения и указания, мы используем ориентиры для определения положения и наведения и так далее, пока поправки не сойдутся, обычно 3 итерации. Однако, если мы находимся в ситуации, когда мы считаем, что ориентиры верны, а наведение / положение камеры неверны, мы просто запускаем только вариант 2.Это то, что делает авторегистрация, когда мы добавляем новые изображения в существующую базу данных ориентиров. Если мы находимся в сценарии, когда мы считаем, что положение / наведение камеры правильное, а не ориентиры, мы запускаем только вариант 1.
Еще одним соображением является относительный вклад каждого ограничения в решение ориентира / положения / указания через дополнительные веса в INIT_LITHOS.TXT, LMKWTS и PICWTS. Например, если модель формы слишком грубая для разрешения карт, с которыми мы работаем, мы можем захотеть уменьшить влияние модели формы как ограничения в решении ориентиров, уменьшив значение WR в INIT_LITHOS.ТЕКСТ. Если мы считаем, что состояние S / C очень хорошо известно по сравнению с ориентирами, мы можем захотеть не позволять ориентирам сильно изменять положение камеры, либо используя очень небольшую неопределенность положения в номиналах, либо дополнительно уменьшая стоимость ВБ в PICWTS.
Рисунок 00: Иллюстрация итеративного процесса обновления геометрии
(Составлено TC)
CategoryPrograms
Геометрическое моделирование - zxc.вики
Геометрическое моделирование, также английский компьютерный геометрический дизайн известный (CAGD) относится к компьютерному описанию формы геометрических объектов. Он занимается описанием двумерных кривых, а также трехмерных поверхностей и тел. Геометрическое моделирование используется в компьютерной графике, автоматизированном проектировании (САПР), методе конечных элементов. и другие инженерные и научные направления.
Кривые и поверхности произвольной формы
Компьютерная анимация для пластиковой иллюстрации поверхности произвольной формыКривые и поверхности произвольной формы могут быть описаны с помощью сплайнов, что означает здесь кусочно-полиномиальные функции.Принцип может быть расширен от двумерных кривых до трехмерных поверхностей.
Кривые Эрмита
Кубические эрмитовы кривые состоят из эрмитовых полиномов третьей степени. Каждый полином определяется начальной и конечной точкой и соответствующей касательной. Когда эрмитовы многочлены складываются в сплайн, касательные двух соседних многоугольников равны. Возможны различные варианты выбора касательных. Самый простой - приравнять касательную к прямой, соединяющей ближайшие контрольные точки, но были разработаны и другие методы:
- Для кардинальных шлицев касательные определяются параметром c между 0 и 1, который определяет «натяжение» в контрольной точке.
- Сплайны Катмулла-Рома - это частный случай кардинальных сплайнов, где c = 0. Они часто используются в качестве анимационных кривых в компьютерной анимации, потому что они проходят точно через контрольные точки и их получение непрерывно.
- Шлицы Кочанека-Бартелса , также называемые шлицами TCB, предлагают дополнительную параметризацию кривых Эрмита с тремя параметрами: натяжение , непрерывность и смещение .
Кривые Безье
Кривые Безье (красные) степеней 1, 2 и 3 и связанные с ними управляющие многоугольникиКривая Безье n - градуса - это параметрическая кривая, определяемая контрольными точками n +1.Многоугольник, соединяющий контрольные точки, называется контрольным многоугольником. В то время как линейная кривая Безье, то есть кривая Безье первой степени, представляет собой простой отрезок между двумя контрольными точками, квадратичная кривая Безье описывает часть параболы. Многие графические программы используют кубические кривые Безье.
Кривая Безье интерполирует между отдельными контрольными точками с использованием полиномов Бернштейна, которые показывают влияние контрольных точек как функцию параметров кривой.За исключением начальной и конечной точек, кривая обычно не проходит через контрольные точки, а содержится в их выпуклой оболочке. Алгоритм Де Кастельжау можно использовать для построения кривой Безье, которая аппроксимирует кривую Безье с помощью многоугольника.
Кривые Безье инвариантны относительно аффинных отображений. Это означает, что аффинное отображение контрольных точек дает ту же кривую, что и аффинное отображение исходной кривой. Проблема с кривыми Безье заключается в том, что при определенном положении контрольных точек возможны точки касания или двоеточия.Локальные изменения контрольных точек оказывают нежелательное влияние на всю кривую, но имеют только локальное значение.
B-сплайновые кривые и NURBS
Модель, составленная из поверхностей NURBSПо сравнению с кривыми Безье, кривые B-сплайна обеспечивают лучшую локальность и управляемость: изменения имеют только локальный эффект, и только часть кривой требует пересчета. Подобно кривым Эрмита, кривые B-сплайна собираются вместе из отдельных полиномов. Швы называются узлами .Таким образом избегаются нежелательные колебания (феномен Рунге) с большим количеством узлов. Кривые B-сплайна представляют собой линейно взвешенную комбинацию основных функций, называемых B-сплайнами. Базисные функции представляют собой кусочно-полиномы с малым носителем. Изменения за пределами балки не влияют на кривую B-сплайна.
Унифицированные базовые функции - это сдвинутые копии друг друга, каждая из которых сосредоточена на узле. Однородные линейные базисные функции - это треугольные функции, которые сосредоточены в определенном узле и имеют поддержку, которая распространяется на три узла.Квадратичные и кубические базисные функции состоят из полиномов более высокого порядка, но всегда с центром в узле. Напротив, неоднородные базисные функции имеют разные формы. Кривые B-сплайна могут быть преобразованы в многоугольник с помощью алгоритма Де-Бура.
Расширением являются рациональных кривых B-сплайнов или, в общем, неоднородные рациональные B-сплайны (NURBS), параметрическое представление которых представляет собой математическую дробь. NURBS достаточно общие, чтобы описывать все общие кривые и поверхности.Некоторые новые инструменты моделирования используют его как единственный внутренний метод представления.
Схемы представлений
Были разработаны различные методы представления тел (схемы представления), которые различаются требованиями к хранению, числовой точностью, сложностью и возможностью преобразования в другие схемы представления. Еще одним свойством схемы представления является возможность проверки правильности модели, то есть определения «реального», физически возможного объекта.
Различают схемы прямого представления, которые описывают сам объем, и косвенные схемы, в которых описание происходит через края и поверхности. Возможны также гибридные схемы, сочетающие оба метода.
Схемы прямого представления
Схема подсчета нормальных ячеек
В схеме перечисления нормальных ячеек пространство делится на равномерно разделенную сетку ячеек (вокселей). Тело представлено набором ячеек.Чем меньше вокселы, тем лучше аппроксимируется тело. Схема перечисления занимает много памяти.
Конструктивная твердотельная геометрия
С помощью конструктивной твердотельной геометрии (CSG) объекты моделируются с помощью основных тел, таких как сферы, кубоиды или цилиндры, а также таких операторов, как пересечение, объединение или разность. Тело CSG можно описать с помощью формулы, которая применяет операторы к основным телам и проиллюстрировать в виде дерева.
CSG особенно распространен в области CAD.Исследование пришло к выводу, что 63% всех механических компонентов можно моделировать с помощью системы CSG, в которой используются только кубоиды и прямые круговые цилиндры. Если разрешено больше основных тел, 90% всех компонентов в классическом машиностроении (в первую очередь, сверление, фрезерование, токарная обработка компонентов или их форм) можно естественным образом описать с помощью CSG.
Большим преимуществом CSG по сравнению с другими схемами отображения является то, что их правильность гарантируется при условии, что разрешены только определенные базовые тела.Если, например, в качестве основного тела используются R-наборы, их свойства гарантируют правильность соответствующего дерева CSG. Кроме того, корпуса CSG очень компактны и просты в производстве. Однако многие методы рендеринга не могут иметь дело с CSG напрямую и требуют, чтобы тела CSG сначала были преобразованы в B-репы, что является сравнительно сложной задачей.
До 1980-х годов большинство инструментов моделирования были основаны либо на граничных представлениях, либо на CSG.
Генеративное моделирование
Генеративное моделирование объектаГенеративная модель - это форма, созданная путем непрерывного преобразования формы, называемая генератором .Размер модели значения не имеет. Моделирование происходит на высоком уровне и может быть расширено. С помощью такого языка программирования, как язык генеративного моделирования, пользователь может легко создать библиотеку полезных форм.
Геометрия сдвига, также называемая разверток , является частным случаем генеративных моделей. Они создаются путем перемещения кривой или объема по кривой.
Особым случаем движений являются поверхности вращения, которые создаются путем вращения на определенную величину вокруг любой оси.
Сетка вокселей
Сетки вокселей представляют собой пространственные и подобные сетке упорядоченные значения, которые описывают «плотность» объекта и могут быть представлены с использованием средств объемной графики. Воксельные сетки позволяют «вырезать» части объектов и заглядывать внутрь. Операции CSG также легко реализовать. Однако воксельные решетки требуют много места для хранения и, как правило, имеют нежелательные эффекты наложения спектров. В некоторых приложениях повышенные требования к памяти можно уменьшить, используя октодеревья.Моделирование с использованием воксельных сеток в основном используется в медицине, гидродинамике и представлении природных объектов, таких как облака.
Схемы косвенного представления
Каркасная модель
Каркасная модель определяет тело исключительно по его краям. Эта модель предлагает преимущества с точки зрения скорости, поскольку дисплей очень эффективен. Одна из проблем этой схемы - ее неоднозначность. Каркасная модель может представлять несколько разных тел, потому что неясно, где находятся поверхности.Поэтому расчет маскировки, как и в случае с поверхностями, невозможен, но можно использовать алгоритм линии ореола.
Рендеринг поверхности
Представление поверхности, также называемое Граничное представление или B-rep , представляет собой описание тела на основе его поверхности; Таким образом, повторения B "пустые". B-повторы, вероятно, являются наиболее распространенной схемой представления, используемой в компьютерной графике. В частности, часто используются полигональные сети.
B-повторов хорошо подходят для эффективного рендеринга общих поверхностей и позволяют вносить в модель локальные изменения.Недостатками B-повторов являются высокие требования к памяти и сложность проверки их правильности.
Представление схем на основе так называемых операций Эйлера используются для, по меньшей мере, частичной гарантии правильности при моделировании тел как B-репродукции. Идея состоит в том, чтобы разрешить только так называемые операции Эйлера, которые сохраняют характеристики Эйлера или изменяют их определенным образом.
Техника моделирования
Полигонизация
Многие алгоритмы компьютерной графики, включая некоторые методы рендеринга, работают исключительно с полигональными сетками.Также методы конечных элементов, основанные на этой презентации. Было разработано множество алгоритмов полигонизации, которые дают результаты разного качества. В общем, метод полигонизации должен обеспечивать хорошее приближение формы исходного объекта, создавать многоугольники со сбалансированной формой, которая не является слишком узкой, и учитывать локальную топологию исходного объекта, то есть не создавать никаких промежутков или разрывов. Примеры алгоритмов полигонизации:
- алгоритм разрезания куба М.Шмидт и
- алгоритм отслеживания Э. Хартманна. Пожалуйста, обратитесь к
Тор
триангулированный с алгоритмом отслеживания
метод нарезки кубиками
Физическое моделирование
Ткань, наложенная на мячМетоды моделирования, учитывающие динамические свойства объектов в дополнение к статическим, называются физически основанными. Объекты могут быть не только жесткими, но и гибкими. Примером может служить кусок ткани, который накладывается на другие предметы, и складки которого рассчитываются автоматически.
См. Также
литература
- Стефан Абрамовски, Генрих Мюллер: Геометрическое моделирование. BI Wissenschaftsverlag, Мангейм 1991
- Макс Агостон: Компьютерная графика и геометрическое моделирование: реализация и алгоритмы. Springer, Лондон 2005, ISBN 1-85233-818-0
- Макс Агостон: Компьютерная графика и геометрическое моделирование: математика. Springer, Лондон 2005, ISBN 1-85233-817-2
- Джеральд Фарин: Кривые и поверхности для компьютерного геометрического проектирования. Academic Press, Сан-Диего 1997, ISBN 0-12-249054-1
- Йозеф Хошек, Дитер Лассер: Основы обработки геометрических данных. Teubner, Штутгарт 1992, ISBN 3-519-12962-0
- Майкл Мортенсон: Геометрическое моделирование. Industrial Press, Нью-Йорк 2006, ISBN 0-8311-3298-1
Интернет-ссылки
Ссылки и комментарии
- ↑ «B-сплайны» часто используются для описания не только основных функций, но и составленных из них B-сплайнов.
 Сравнительное измерение является универсальным самым быстрым и лёгким методом проверки геометрии повреждённого кузова. Производятся сравнения диагональных расстояний между симметричными точками. Можно измерять, сравнивая повреждённую часть автомобиля с неповреждённой.
Сравнительное измерение является универсальным самым быстрым и лёгким методом проверки геометрии повреждённого кузова. Производятся сравнения диагональных расстояний между симметричными точками. Можно измерять, сравнивая повреждённую часть автомобиля с неповреждённой. Это бывает необходимым, когда есть конкретные данные расстояний между контрольными точками для измерительной линейки. Нужно учитывать, что в некоторых руководствах по ремонту показаны расстояния для измерительной линейки (значениями на шкале линейки), а в других расстояния от точки к точке (фактическое расстояние). Это могут быть разные значения.
Это бывает необходимым, когда есть конкретные данные расстояний между контрольными точками для измерительной линейки. Нужно учитывать, что в некоторых руководствах по ремонту показаны расстояния для измерительной линейки (значениями на шкале линейки), а в других расстояния от точки к точке (фактическое расстояние). Это могут быть разные значения.
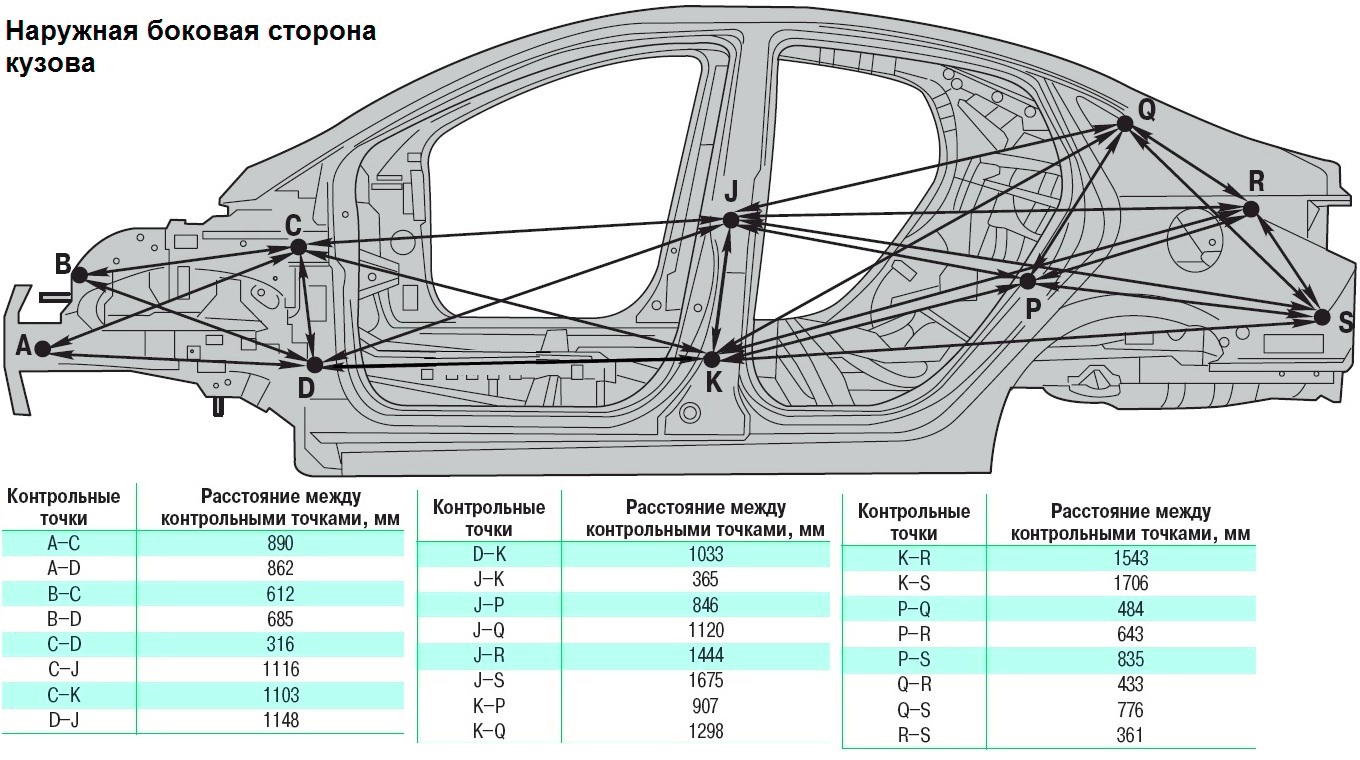 Расстояние между креплениями делается от центра к центру (к примеру, между центрами головок болтов).
Расстояние между креплениями делается от центра к центру (к примеру, между центрами головок болтов).
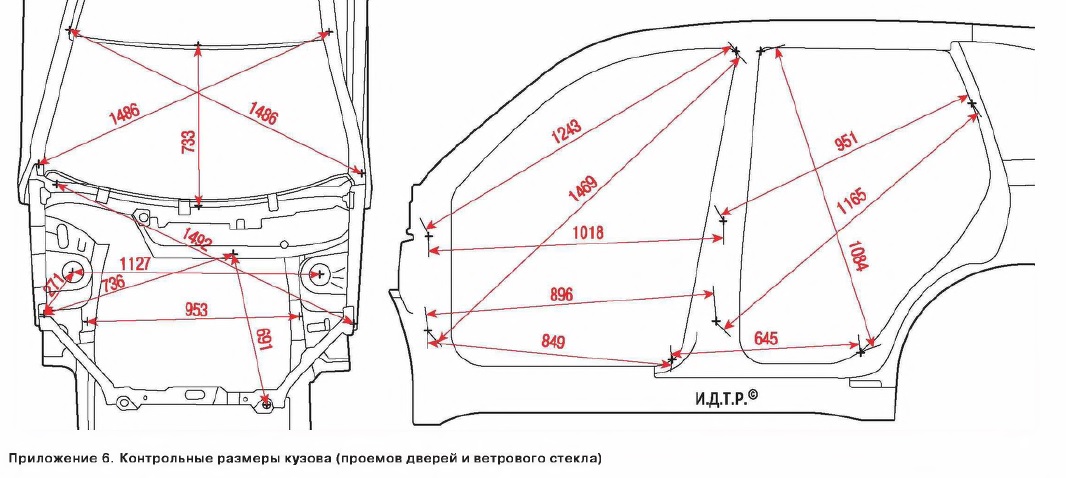
 Их еще называют жестяными работами;
Их еще называют жестяными работами; Именно из-за этого, как правило, чаще всего нарушается геометрия ВАЗ 2110;
Именно из-за этого, как правило, чаще всего нарушается геометрия ВАЗ 2110;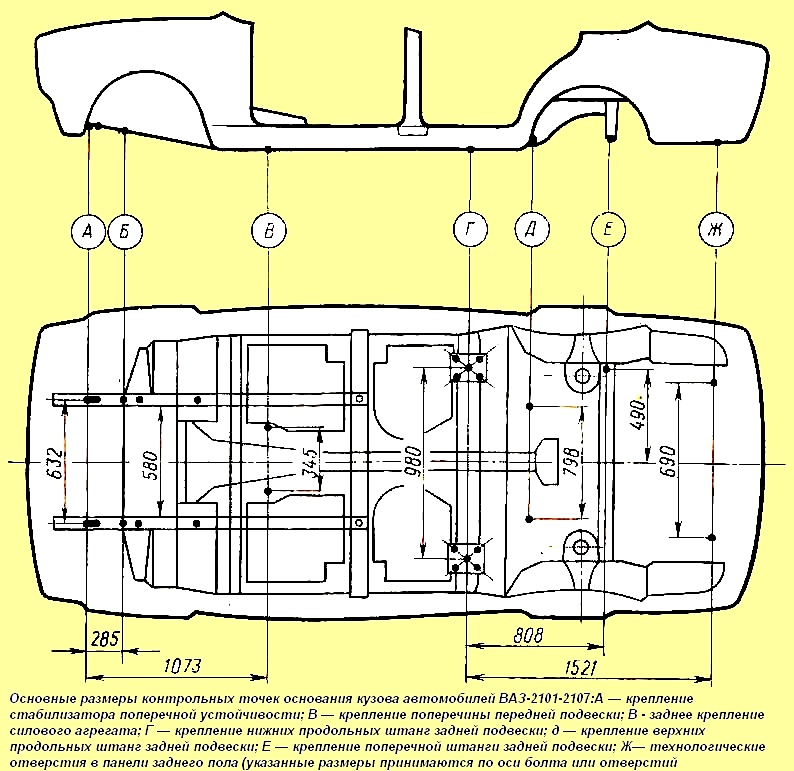
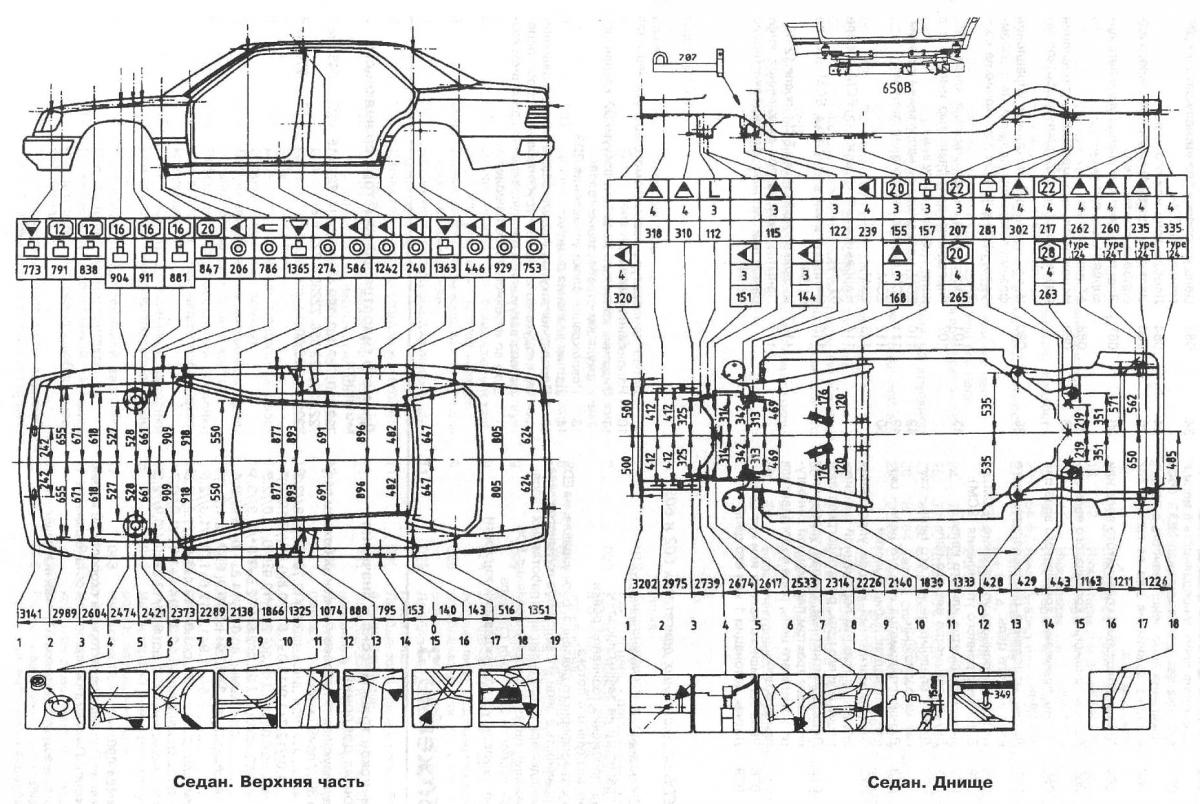
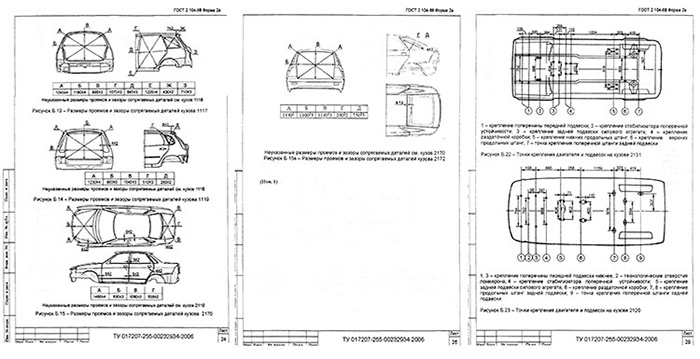 Щелкните треугольник раскрытия, чтобы открыть отдельные ползунки ширины и высоты.
Щелкните треугольник раскрытия, чтобы открыть отдельные ползунки ширины и высоты.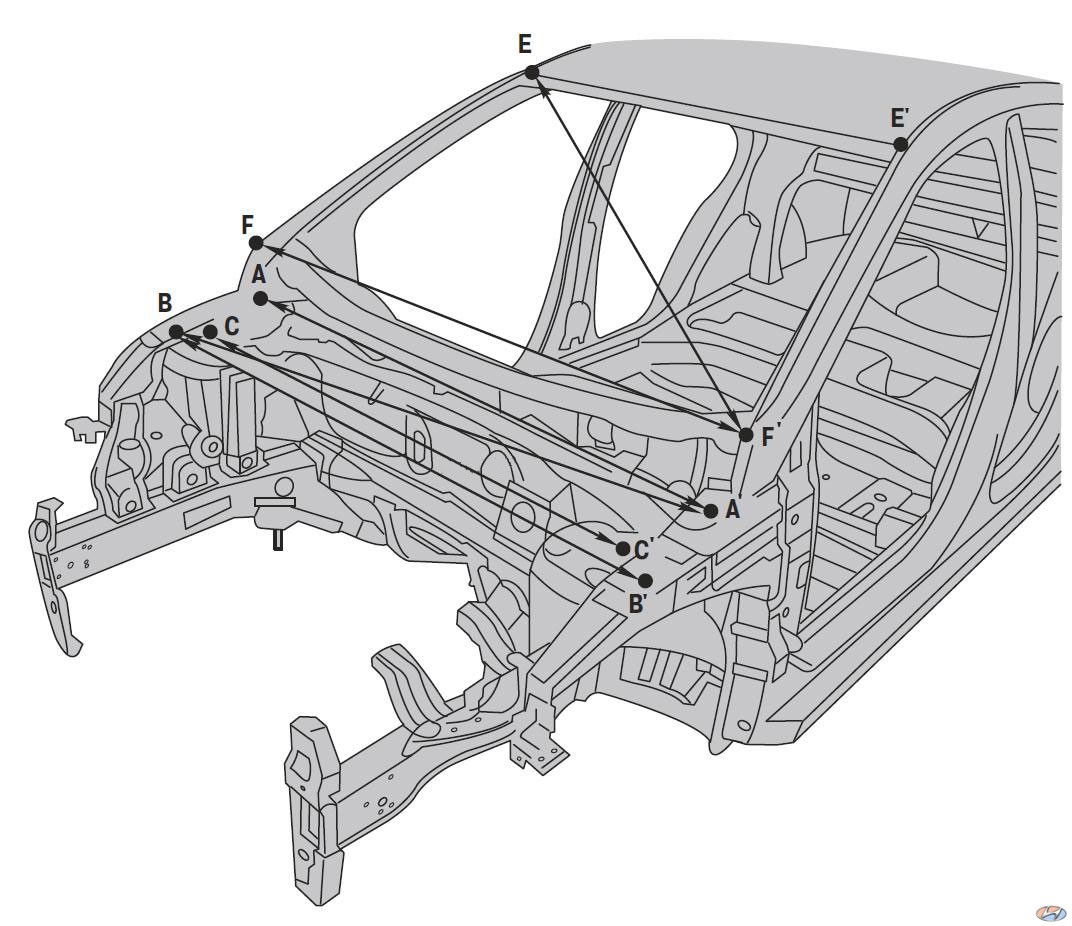 Контрольные точки B-сплайна лежат внутри, снаружи или на краю фигуры и соединены рамкой B-сплайна.
Контрольные точки B-сплайна лежат внутри, снаружи или на краю фигуры и соединены рамкой B-сплайна. Большинство крупных университетов преподают математику и информатику геометрии NURBS. Это означает, что поставщики специализированного программного обеспечения, группы инженеров, фирмы промышленного дизайна и анимационные компании, которым необходимо создавать собственные программные приложения, могут найти обученных программистов, способных работать с геометрией NURBS.
Большинство крупных университетов преподают математику и информатику геометрии NURBS. Это означает, что поставщики специализированного программного обеспечения, группы инженеров, фирмы промышленного дизайна и анимационные компании, которым необходимо создавать собственные программные приложения, могут найти обученных программистов, способных работать с геометрией NURBS.
 Значение по умолчанию — 0 (ноль) градусов (на восток). Угол рассчитывается против часовой стрелки.
Значение по умолчанию — 0 (ноль) градусов (на восток). Угол рассчитывается против часовой стрелки. Число по умолчанию — 4. При указании значения 3 получается треугольник. Если указать значение меньше 3, получится круг.
Число по умолчанию — 4. При указании значения 3 получается треугольник. Если указать значение меньше 3, получится круг. Блок отображает стрелку с закрытым концом. Open Ended — это блочная стрелка с открытым концом. Зачеркнутый означает, что в теле стрелки будет помещен крест. Значение по умолчанию — Open Ended.
Блок отображает стрелку с закрытым концом. Open Ended — это блочная стрелка с открытым концом. Зачеркнутый означает, что в теле стрелки будет помещен крест. Значение по умолчанию — Open Ended. При этом символ штриха отображается только на концах строки, а остальная часть строки остается без символов. Значение по умолчанию не отмечено.
При этом символ штриха отображается только на концах строки, а остальная часть строки остается без символов. Значение по умолчанию не отмечено. Пользовательский подгоняет узор по длине элемента, немного изменяя зазоры.Никакое ограничение не регулирует зазоры вообще, а это означает, что шаблон вряд ли точно соответствует длине элемента. По умолчанию используется половинный узор.
Пользовательский подгоняет узор по длине элемента, немного изменяя зазоры.Никакое ограничение не регулирует зазоры вообще, а это означает, что шаблон вряд ли точно соответствует длине элемента. По умолчанию используется половинный узор. Это свойство действует, только если для параметра Endings установлено значение Custom. При построении правила представления этот параметр динамически извлекается из значения Step и динамически обновляется во время построения или модификации правила, когда обновляется свойство Endings.
Это свойство действует, только если для параметра Endings установлено значение Custom. При построении правила представления этот параметр динамически извлекается из значения Step и динамически обновляется во время построения или модификации правила, когда обновляется свойство Endings.
 Значение по умолчанию — Квадрат.
Значение по умолчанию — Квадрат.
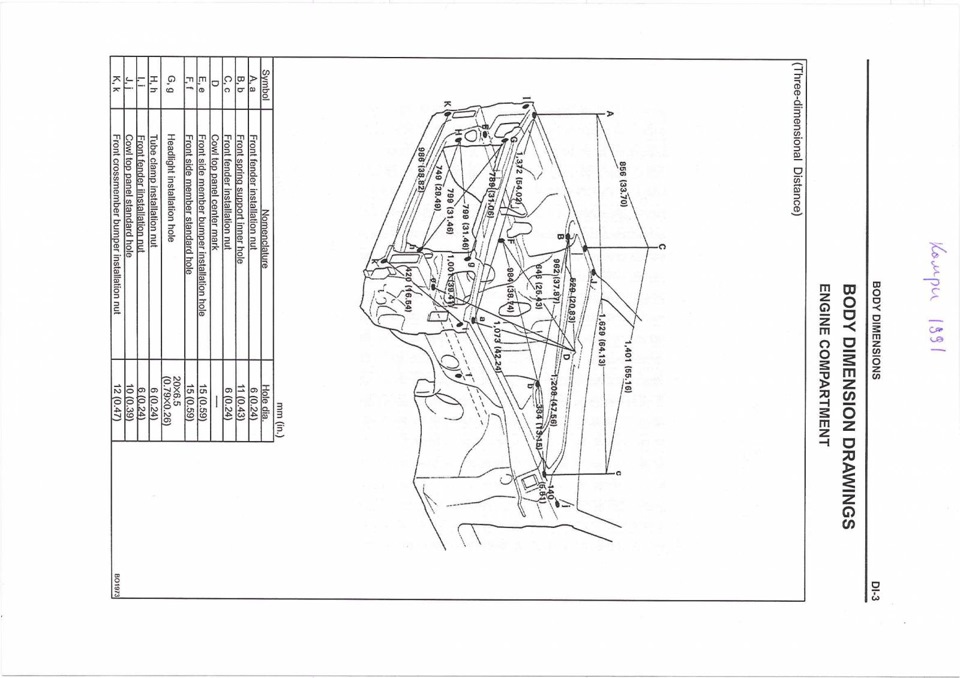 Значение по умолчанию — 10 пунктов. Значение меньше 10 поддерживает большую часть исходной формы штриха. Значение больше 10 сохраняет меньшую исходную форму штриха.
Значение по умолчанию — 10 пунктов. Значение меньше 10 поддерживает большую часть исходной формы штриха. Значение больше 10 сохраняет меньшую исходную форму штриха.